Bagi sebagian besar kalangan, cara menghitung masih terbilang cukup susah, terutama pada jenis bilangan yang asing, seperti desimal. Situasi ini merupakan sebab dari cara menghitung perkalian pecahan yang berbeda menyesuaikan dengan jenis bilangan tersebut dalam matematika. Ingin tahu lebih lanjut? Cari tahu di sini!
Apa Saja Jenis Bilangan Pecahan?
Secara garis besar, pecahan atau fraksi merupakan sebuah istilah dalam dunia matematika. Penggunaan istilah ini untuk menggambarkan sebuah bentuk dari b ≠ 0 yang menandakan bahwa persamaan dalam matematika tersebut memiliki angka pembilang.
Di samping itu, tujuan adanya bilangan pecahan adalah untuk menyederhanakan penyebut dan pembilang, sehingga akan lebih mudah untuk menghitungnya. Sistem ini termasuk dalam sistem perhitungan aritmatika yang mana hasil dari perhitungan tidak akan berjumlah besar. Tetapi, angka dari hasil tersebut bernilai sama.
Selain itu, terdapat berbagai jenis dari bilangan pecahan tersebut yang tidak hanya sebuah bilangan pecahan campuran dan desimal. Anda dapat menyimak penjelasan di bawah ini untuk pemahaman lebih tentang pecahan dan cara menghitung perkalian pecahan.
1. Bilangan Pecahan Biasa atau Sederhana
Macam bilangan pecahan yang pertama adalah pecahan biasa atau sederhana. Seperti namanya, bilangan jenis ini jarang memiliki angka yang banyak dan cukup sederhana. Oleh sebab itu, bilangan satu ini hanya terdapat pembilang dan penyebut.
Sebuah pembilang yang berada pada bagian atas tidak selalu lebih kecil dari penyebut yang berada di bawahnya. Situasi ini hadir karena bentuk dari pecahan bisa terbagi menjadi dua jenis, yaitu pecahan biasa murni dan tidak murni. Contohnya, bilangan ½, ¾, ⅞, dan seterusnya.
Pecahan biasa murni merupakan sebuah bilang pecahan sederhana yang mana angka pembilang lebih kecil dari penyebut (a<b). Sedangkan untuk pecahan sederhana tidak murni memiliki pembilang yang lebih besar dari penyebut (a>b). Sebagai tambahan contoh adalah 9/4, 7/3, 6/5, dan seterusnya.
2. Bilangan Pecahan Campuran
Selanjutnya, bilangan pecahan campuran merupakan sebuah gabungan dari pecahan murni dan bilangan bulat. Contohnya seperti bilangan 1 ½, 5 ⅔, 7 ⅚, dan seterusnya.
3. Bilangan Pecahan Desimal
Bentuk desimal merupakan bilangan yang memiliki tanda (,) di dalam sebuah angka. Koma tersebut merupakan hasil dari perhitungan sebuah bilangan pecahan sederhana, seperti ½ jika dirubah ke desimal maka jadi 0,5.
4. Bilangan Persen dan Permil
Lalu, ada bilangan persen yang memiliki pembilang sebesar 100 dan jumlah dari perhitungannya akan menjadi %. Seperti contohnya, 45/100 yang merupakan bilangan pecahan dari 45%. Sedangkan permil memiliki pembilang 1000 yang memiliki simbol ‰.
Baca Juga : Cara Mudah Mengubah Pecahan Biasa Menjadi Desimal, Simak!
Cara Menghitung Perkalian Pecahan
Setelah memahami konsep dan penjelasan dari bilangan pecahan, Anda harus mempelajari cara menghitung perkalian pecahan sesuai dengan jenis bilangan. Di bawah ini merupakan cara menghitung perkalian pecahan untuk bilangan campuran dan desimal.
a. Perkalian Campuran
Terdapat sebuah soal yang di dalamnya terdapat permintaan untuk menghitung hasil dari 1¼ × 3⅖. Ikuti langkah di bawah ini untuk cara menghitung perkalian pecahan dengan bilangan campuran tersebut.
1. Tentukan Nilai Pecahan Sederhana
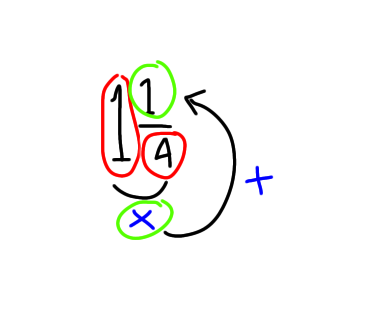
Langkah paling awal, Anda harus mengetahui nilai dari pecahan sederhana bilang 1⅕ dan 3⅖. Caranya mudah, jika Anda ingin mengubah bilangan 1¼ maka Anda harus mengalikan penyebut yaitu 4 dengan angka bulat 1. Lalu, tambahkan hasilnya dengan pembilang 1, maka akan didapat pecahan sederhana dari 1¼ adalah 5/4.
Lakukan langkah yang sama untuk menentukan besar bilangan dari 3⅖, yaitu 17/5.
2. Perkalian Pecahan Sederhana
Selanjutnya, tulis angka dari hasil pecahan sederhana kedua bilangan tersebut dan hitung menggunakan sistem perkalian.
3. Coret Angka yang Sama
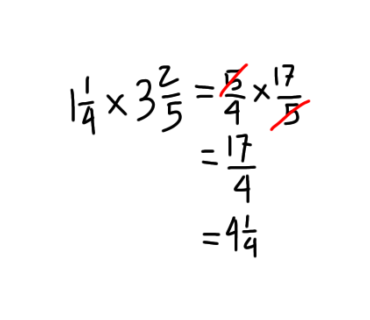
Cara paling mudah saat Anda menemukan besaran angka salah satu pembilang dan angka penyebut lawan sama, maka Anda dapat mencoret keduanya.
4. Ubah Kembali ke Pecahan Campuran
Setelah Anda mendapatkan hasil dari 5/4 × 17/5 yaitu 17/4, lalu ubah kembali bilangan pecahan sederhana tersebut menjadi pecahan campuran. Jadi, hasil dari perhitungan bilangan pecahan campuran 1¼ × 3⅖ dengan cara menghitung perkalian pecahan adalah 4¼.
b. Perkalian Desimal
Terdapat rumus mudah yang dapat Anda pelajari untuk menghitung perkalian desimal dengan cara menghitung perkalian pecahan. Soal contohnya adalah tentukan hasil dari 3,75 × 6,897. Maka, ikutilah cara di bawah ini:
1. Tentukan Banyaknya Angka Desimal
Angka desimal merupakan banyaknya jumlah angka yang berada setelah tanda (,). Langkah awal untuk menentukan hasil dari 3,75 × 6,897 adalah dengan memperhatikan jumlah angka yang berada di belakang tanda (,).
Pada bilangan 3,75 terdapat 2 angka yaitu 7 dan 5, sedangkan untuk bilangan, 6,897 terdapat 3 angka yaitu 8, 9, dan 7.
Banyaknya angka desimal ini perlu Anda ingat dan perhatikan karena ini berfungsi untuk menentukan hasil akhir soal tersebut.
2. Lakukan Perkalian dengan Bilangan Bulat
Kemudian, Anda perlu memulai untuk mengalikan kedua bilangan yang sudah berubah menjadi bilangan bulat tersebut. Cara menghitung perkalian pecahan desimal yang sudah menjadi bulat yaitu dengan cara menghilangkan tanda (,) pada bilangan tersebut.
Jadi, contoh soal di atas menjadi 375 × 6897 yang memiliki hasil 2586375.
3. Jumlahkan Banyak Angka Desimal
Setelah mengetahui jumlah perkalian dari kedua bilangan bulat tersebut, Anda perlu menjumlahkan banyak angka yang terdapat di belakang koma. Jadi, jumlah angka desimal untuk kedua bilangan tersebut sebanyak 5 angka desimal.
4. Tentukan Nilai Desimal
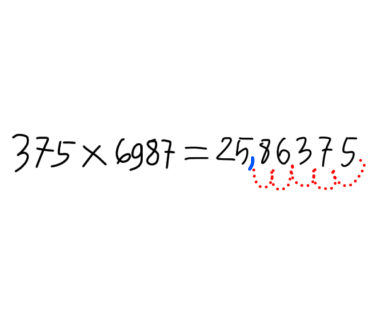
Langkah terakhir adalah ubah kembali bilangan bulat tersebut menjadi sebuah pecahan desimal. Caranya dengan menghitung dan meloncat dari posisi paling belakang menyesuaikan jumlah bilangan desimal dari kedua bilangan tersebut. Maka, hasil dari 3,75 × 6,897 adalah 25,86375.
c. Perkalian Bilangan Campuran dan Desimal
Selanjutnya, Anda dapat mencoba untuk hitung hasil dari bilangan campur dari 0,5 × ¾. Lalu bagaimana caranya mengubah ke bentuk pecahan sederhana? Berikut ini adalah cara pertama dengan mengubahnya menjadi pecahan sederhana.
1. Ubah Menjadi Pecahan Sederhana
Langkah pertama untuk menghitung hasil dari perkalian dua bilangan 0,5 × ¾ adalah dengan mengubah bilangan desimal menjadi pecahan sederhana. Hakikatnya, bilangan desimal memiliki penyebut 10, 100, dan kelipatannya.
Besaran penyebut bilangan desimal tersebut menyesuaikan dengan besaran angka belakang koma. Jika bilangan desimalnya adalah 0,5 maka pecahan sederhananya adalah 5/10.
2. Kalikan Kedua Pecahan Sederhana
Anda sudah mendapatkan dua bilangan pecahan sederhana yaitu 5/10 × ¾. Jadi, Anda bisa mengalikan kedua bilangan tersebut hingga membuahkan hasil 15/40.
3. Sederhanakan Hasil
Anda mendapatkan hasil berupa bilangan pecahan sederhana, walaupun dengan angka yang besar. Pada bilangan pecahan 15/40, Anda dapat membagikan dengan kelipatan terbesar yang bisa membagi keduanya, yaitu angka 5 menjadi ⅜. Jadi, hasil dari 0,5 × ¾ dengan bentuk pecahan sederhana adalah ⅜.
Selanjutnya, di bawah ini merupakan cara untuk mengubah hasil dari 0,5 × ¾ menjadi sebuah bilangan desimal.
4. Ubah Menjadi Bilangan Desimal
Pertama, Anda harus mengubah salah satu bilangan pecahan menjadi desimal, yaitu ¾. Ubah bilangan tersebut menjadi desimal dengan menjadikan perseratus, sehingga hasilnya 75/100 = 0,75.
5. Kalikan dengan Cara Perkalian Desimal
Selanjutnya, ikuti cara menghitung perkalian pecahan desimal di atas. Maka, hasil yang Anda dapatkan dari 0,5 × ¾ adalah 0,375.
Baca Juga : Operasi Perkalian Bilangan Bulat: Pengertian, Rumus, Contoh Soal & Pembahasan
Masih Kesulitan dengan Cara Menghitung Perkalian Pecahan?
Banyak kalangan beranggapan bahwa perhitungan matematika selalu menjadi hal yang sulit untuk dimengerti. Tetapi, perlu Anda ketahui bahwa terdapat cara menghitung perkalian pecahan yang sangat mudah untuk Anda pahami dan pelajari. Kunci dari pemahaman tersebut adalah ketahui jenis pecahan.
Jenis pecahan sangat beragam, sehingga terdapat rumus yang beragam pula untuk diimplementasikan ke dalam hitungan matematika. Walaupun begitu, jika Anda sudah paham jenis dari pecahan tersebut, maka Anda dapat menghitung perkalian pecahan tersebut dengan mudah.

