Lingkaran merupakan salah satu pelajaran matematika geometri yang punya banyak konsep. Persinggungan garis terhadap dua atau satu lingkaran juga bagian dari ilmu geometri. Kamu bisa mencari rumus garis singgung persekutuan luar untuk menyelesaikan problematika tersebut. Ketahui penjelasan lengkapnya di artikel ini!
Apa Itu Garis Singgung Lingkaran?
Sebelum membahas rumus garis singgung persekutuan luar, ada baiknya kamu memahami apa itu garis singgung lingkaran terlebih dahulu.
Garis singgung lingkaran adalah materi lanjutan dari bangun datar dua dimensi yang mana bisa disebut sebagai garis yang memotong lingkaran. Garis yang berada tepat menyinggung satu titik lingkaran disebut sebagai titik singgung lingkaran.
Secara spesifik, garis singgung ini dapat dibedakan berdasarkan lokasi garisnya. Ada tiga macam letak garis pada lingkaran, yaitu:
- Garis yang memotong dua titik lingkaran.
- Garis yang menyinggung satu titik lingkaran.
- Terakhir, garis yang berada di luar lingkaran tanpa ada perpotongan atau persinggungan dengan lingkaran.
Berikut ini ilustrasinya:
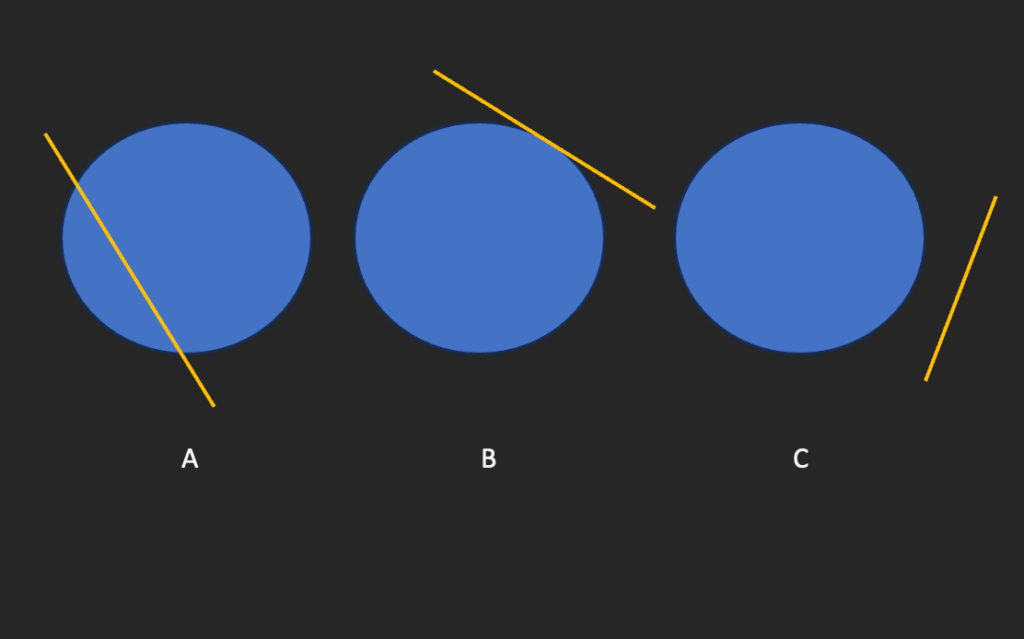
Sehingga, maksud dari garis singgung persekutuan luar adalah suatu garis yang menyinggung satu titik dalam lingkaran. Secara teori, terdapat garis singgung persekutuan luar dalam satu lingkaran dan dua lingkaran dengan rumus yang berbeda.
Adapun beberapa ciri dan sifat dalam garis singgung lingkaran adalah sebagai berikut:
- Garis singgung menyentuh lingkaran dalam satu titik.
- Jika garis singgung melalui dua titik lingkaran, maka bisa dibuat dua garis singgung lingkaran.
- Apabila dua garis singgung berpotongan di luar lingkaran, maka nilai titik-titik singgung lingkaran kedua garis tersebut adalah sama.
- Letak garis singgung lingkaran adalah tegak lurus dengan jari-jari di titik singgungnya.
- Garis singgung dan jari-jari lingkaran membentuk sudut 90o.
Cara Menentukan Rumus Garis Singgung Persekutuan Luar
Berdasarkan pengertian di atas, terdapat dua macam rumus garis singgung persekutuan luar pada satu lingkaran dan dua lingkaran. Berikut ini penjelasannya:
1. Garis Singgung Persekutuan Luar dalam Satu Lingkaran
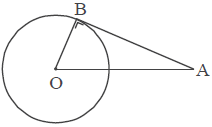
Gambar di atas merupakan garis singgung persekutuan luar pada satu lingkaran, di mana hanya ada satu lingkaran dan garisnya hanya menyinggung satu titik lingkaran. Oleh karena itu, jari-jarinya akan terletak pada garis OB dan tegak lurus dengan garis singgung AB.
Berdasarkan penjelasan tersebut, garis AOB membentuk bangun datar segitiga siku-siku. Sehingga, rumus garis singgung persekutuan luar ini bisa menggunakan Teorema Phytagoras seperti berikut:
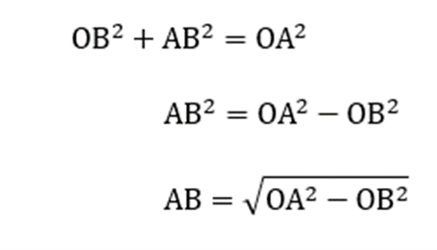
2. Garis Singgung Persekutuan Luar Dua Lingkaran
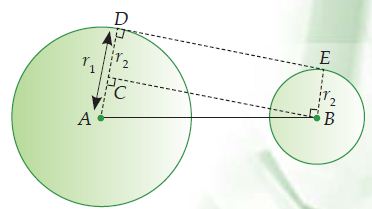
Gambar di atas tentu berbeda dengan gambar sebelumnya. Kamu bisa lihat terdapat dua lingkaran yang terhubung oleh garis singgung.
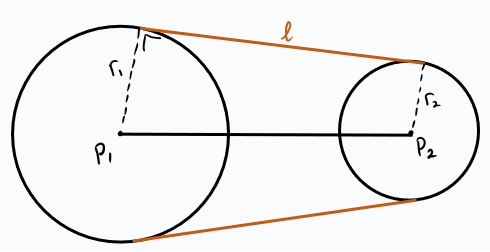
Dalam gambar di atas, garis AB merupakan jarak antara kedua titik pusat lingkaran (s). Garis DE merupakan garis singgung persekutuan luar dua lingkaran yang tegak lurus dengan AD.
Jari-jari lingkaran pertama ditandai dengan r1, sedangkan jari-jari lingkaran kedua ditandai dengan r2. Terdapat garis BC yang menarik titik pusat dengan titik tengah jari-jari (r1) yang menyebabkan terbentuknya sudut siku-siku sudut 90o pada ACB.
Garis BC juga sejajar dengan DE, sehingga membentuk jari-jari yang sama antara DC dan EB (r2) dan terbentuklah segitiga siku-siku. Dengan demikian, rumus garis singgung persekutuan luar pada kasus ini akan menggunakan Teorema Phytagoras seperti berikut:

Berdasarkan rumus di atas, kamu bisa menentukan garis singgung persekutuan luar dengan mengetahui jarak kedua pusat lingkaran (AB) dan panjang jari-jari dari masing-masing lingkaran.
Baca Juga : Rumus Garis Singgung Persekutuan Dalam serta Contoh Soalnya
Contoh Soal Penerapan Rumus Garis Singgung Persekutuan Luar
Setelah memahami beberapa uraian di atas, kamu bisa memantapkan pemahaman melalui beberapa latihan soal berikut ini:
1. Contoh Soal Pertama
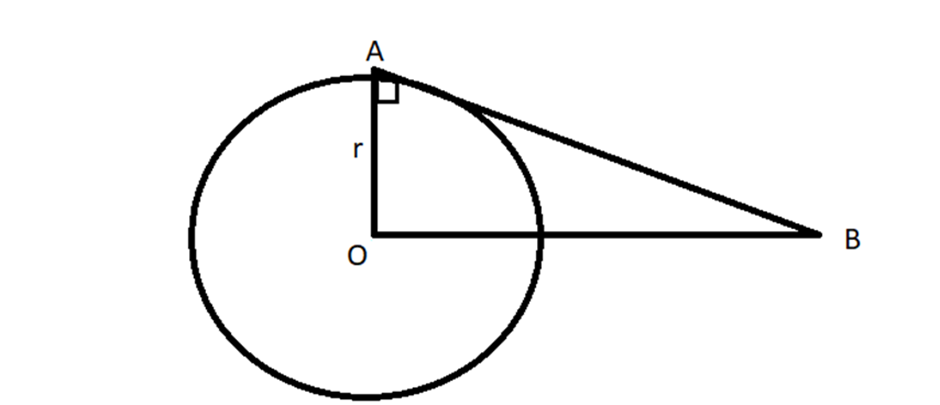
Perhatikan gambar di atas, jika jari-jari lingkaran (r) sebesar 8 cm dan OB sebesar 10 cm, maka tentukanlah:
a. panjang garis singgung pada AB
b. luas segitiga AOB
Jawab:
Berdasarkan rumus garis singgung persekutuan luar sebelumnya, AB merupakan garis singgung persekutuan luar. Sehingga, kamu bisa menggunakan Teorema Phytagoras seperti berikut:
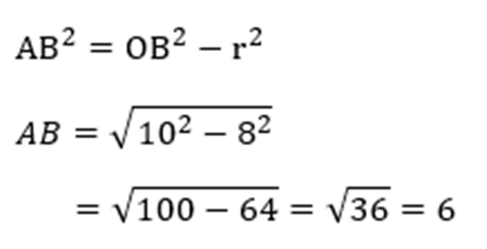
Kemudian, soal kedua bisa kamu hitung menggunakan rumus luas segitiga. Berikut ini caranya:
Luas segitiga OAB = ½ x OA x AB
Luas segitiga OAB = ½ x 8 x 6 = 24 cm2
2. Contoh Soal Kedua
Terdapat garis singgung persekutuan luar pada dua lingkaran dengan panjang 12 cm dan jarak titik pusat antar kedua lingkaran tersebut adalah 15 cm. Jika diketahui panjang salah satu jari-jari lingkaran adalah 4 cm, maka hitunglah panjang jari-jari lainnya.
Jawab:
Diketahui:
- Garis singgung persekutuan luar (d) = 12 cm
- Jarak titik pusat kedua lingkaran (p) = 15 cm
- Salah satu panjang jari-jari (r) = 4 cm
Maka, panjang jari-jari lainnya (R) adalah:
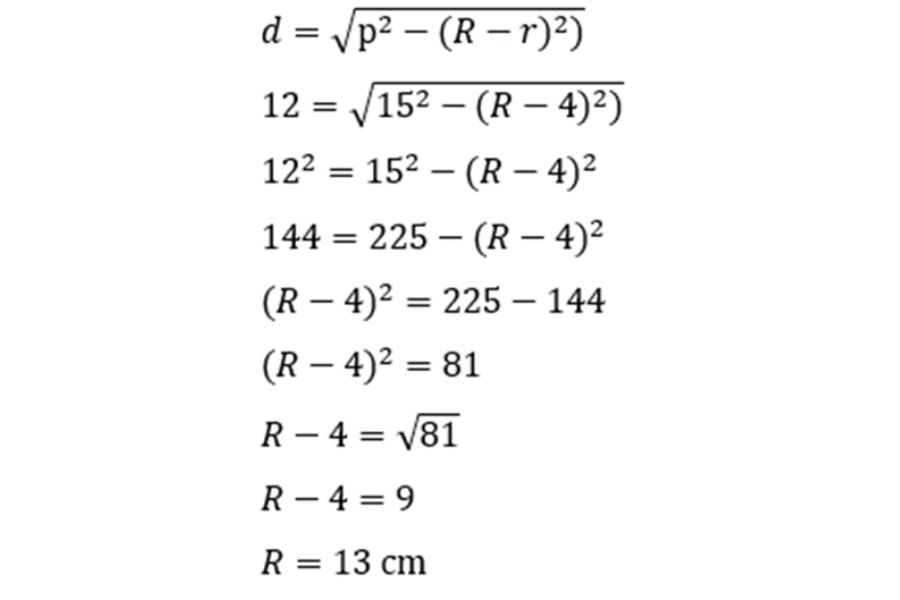
3. Contoh Soal Ketiga
Diketahui terdapat layang-layang dan lingkaran, di mana panjang jari-jari OL = OK sebesar 8 cm sedangkan jarak titik pusat ke luar garis singgung (OM) adalah 17 cm. Tentukanlah:
a. Panjang KM
b. Panjang KL
Jawab:
a. Garis KM merupakan garis singgung persekutuan luar, sehingga kamu harus menggunakan rumus garis singgung persekutuan luar yaitu Teorema Phytagoras.
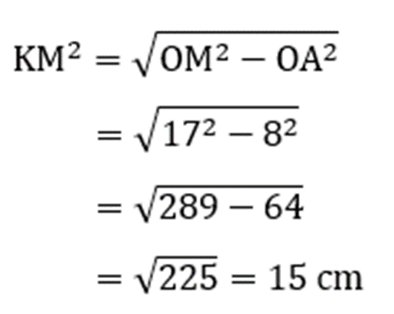
b. Garis KL merupakan bangun layang-layang dari KOLM. Jadi, kamu bisa menggunakan perbandingan rumus luas layang-layang dan luas segitiga. Sebab, garis KL juga merupakan bagian dari segitiga KOL. Berikut penjabaran rumusnya:
Luas layang-layang KOLM = 2 x Luas segitiga KOL
½ x OM x KL = 2 x ½ x OL x LM
½ x 17 x CA = 8 x 15
CA = 14,11 cm
4. Contoh Soal Keempat
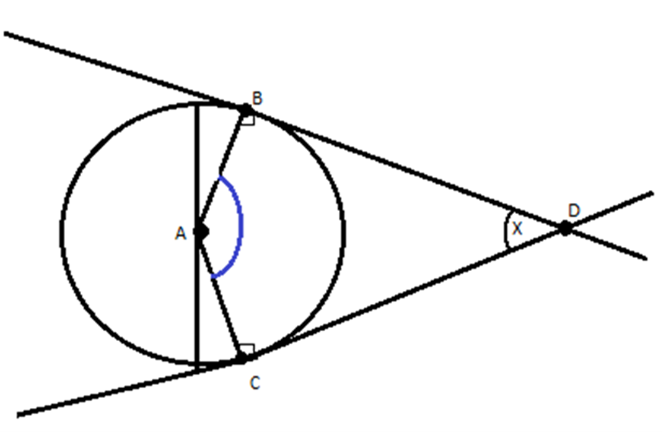
Pada gambar di atas, garis singgung lingkaran persekutuan luar membentuk sudut BCD. Jika sudut BAC adalah 147o, maka tentukanlah sudut BCD!
Jawab:
Dari gambar di atas, kamu bisa mengetahui sudut DAC dan BAD adalah 90o. Sebab, pada gambar terdapat siku-siku di sudut B dan C.
Untuk menentukan sudut BCD, kamu harus menjumlahkan sudut-sudut yang ada di dalam bangun tersebut, kemudian menguranginya dengan sudut satu lingkaran penuh, yaitu 360o. Berikut caranya:
∠ABD + ∠BDC + ∠DCA + ∠BAC = 360o
90o + x + 90o + 147o = 360o
x = 33o
5. Contoh Soal Kelima
Terdapat dua lingkaran yang memiliki titik pusat P dan Q dengan jarak 26 cm. Jari-jari lingkaran tersebut sebesar 12 cm dan 2 cm. Hitunglah berapa panjang garis persekutuan luar kedua lingkaran tersebut?
Jawab:
Dari data pada soal, kamu bisa mengetahui bahwa:
- Jarak titik pusat kedua lingkaran (p) = 26 cm
- Jari-jari pertama (r) = 12 cm
- Jari-jari kedua (R) = 2 cm
Maka, panjang garis persekutuan luar (d) adalah:
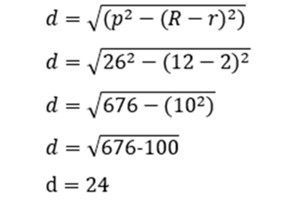
Sudah Paham dengan Rumus Garis Singgung Persekutuan Luar?
Demikian penjelasan lengkap mengenai materi rumus garis singgung persekutuan luar yang merupakan cabang dari ilmu geometri. Dari penjelasan di atas, kamu bisa tahu garis singgung persekutuan luar adalah garis yang dibentangkan akan menyinggung lingkaran dalam satu titik.
Berdasarkan sifat-sifatnya, kamu bisa menemukan karakteristiknya sendiri untuk memperkaya pemahaman terkait materi ini. Selain itu, latihan dengan variasi soal juga akan melatih daya pikir agar lebih kritis dalam menyelesaikan konsep soal.
Pada intinya, hal yang paling penting untuk kamu bisa lancar mengerjakannya adalah pemahaman terkait Teorema Phytagoras. Selamat belajar!