Tentu kamu tidak asing dengan turunan, bukan? Ternyata, turunan ini mempunyai kebalikan loh, namanya integral. Pada artikel ini, kamu yang suka sama matematika akan diajak mengenal apa itu integral khususnya contoh soal integral tak tentu. Yuk, simak pembahasannya di sini!
Pengertian Integral
Supaya mengingat kembali cara mengoperasikan integral, kamu coba ingat juga mengenai fungsi turunan. Jadi, pastikan kamu tahu cara penyelesaiannya.
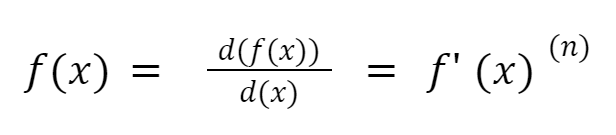
Untuk mengoperasikan turunan pada fungsi turunan di atas, kamu bisa memperhatikan pangkat (n) dari sebuah fungsi f(x) lalu mengalikan ke depan kemudian pangkat (n) tersebut dikurangi satu.
Contohnya:
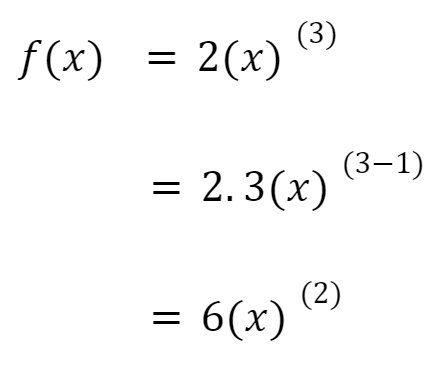
Bagaimana sudahkah ingat kamu mengenai turunan? Jika sudah, mari kita bahas apa itu integral. Fungsi Integral adalah bentuk penjumlahan yang saling berhubungan dengan turunan (kebalikan dari turunan).
Para pakar matematikawan biasanya memakai integral agar memudahkan pekerjaan mereka dalam mencari diferensial (turunan). Adapun persamaan fungsi dari integral yakni sebagai berikut.

Jadi, rumus integral itu tidak bisa berdiri sendiri ya! Mereka bergantung dengan turunan. Maka dari itu, kamu wajib hafal konsep dasar integral terlebih dahulu.
Dalam suatu integral dari suatu fungsi dibagi menjadi 2 yaitu integral tentu dan tak tentu. Nah, kali ini kamu akan mempelajari integral tak tentu. Jadi, pahami dan pelajari dengan baik penjelasan yang akan kamu baca di bawah ini!
Pengertian Integral Tak Tentu

Integral tak tentu adalah integral yang tak memiliki batas. Integral ini adalah proses yang menentukan bentuk umum dari turunan dari suatu fungsi f(x). Inilah fungsi dari integral tak tentu.
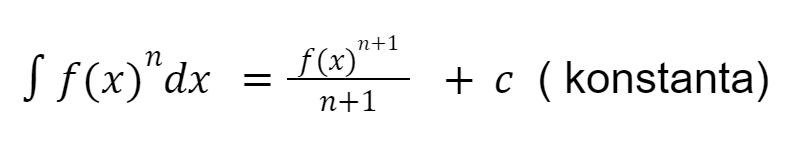
Pada rumus di atas, dapat kamu lihat huruf c. Huruf tersebut adalah konstanta yang bebas ketentuannya.
5 Kaidah dari Integral Tak Tentu
Dalam integral tak tentu ini, terdapat beberapa kaidah yang dapat kamu ingat agar mudah saat mengerjakan soal integral. Berikut 5 sifat dari integral tak tentu beserta rumusnya, yakni:
1. Kaidah Pangkat
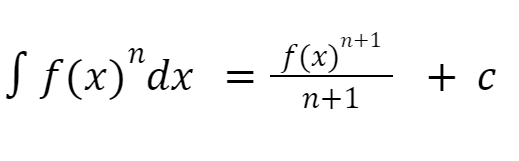
2. Kaidah Logaritma
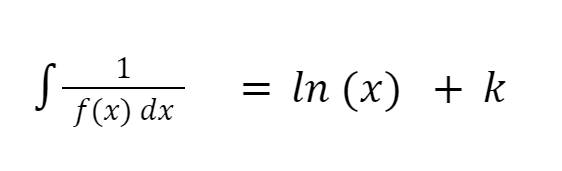
3. Kaidah Polinomial ( Penjumlahan dan Pengurangan)
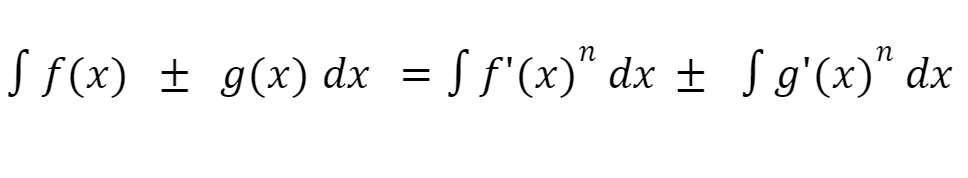
4. Kaidah Eksponensial
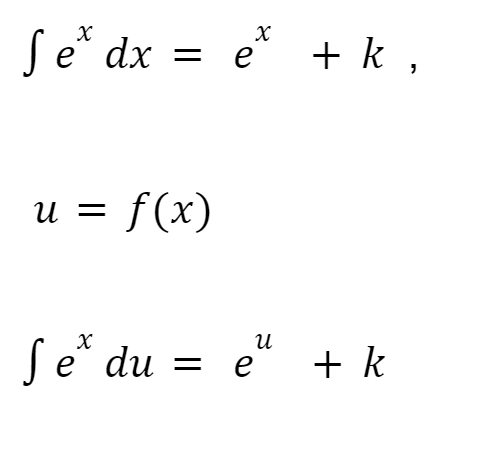
5. Kaidah Perkamu
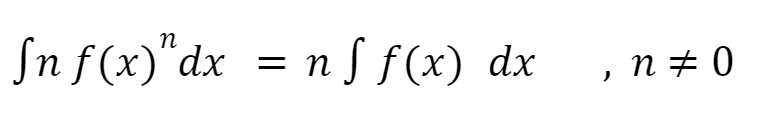
Fungsi dari Integral Tak Tentu
Sebenarnya, banyak sekali manfaat yang dapat kamu gunakan dari mempelajari integral tak tentu. Salah satunya yaitu menyelesaikan persamaan kurva dari suatu fungsi.
Namun, kamu harus terlebih dahulu menemukan turunannya atau persamaan gradien dari garis yang menyinggung pada kurva baru menyelesaikan integralnya.
Integral tak tentu ini juga berfungsi dalam berbagai pelajaran loh, seperti fisika. Aplikasi ini sering dipakai dalam mencari kecepatan dan percepatan suatu kendaraan.
Berikut contoh soal integral tak tentu dalam menentukan kecepatan dan percepatan.
Suatu kendaraan pada t=10 detik akan melaju dengan kecepatan 10 m/s dengan percepatan a(t) = 4t-5. Maka berapa jarak yang ditempuh pada t =3 detik menggunakan kecepatan yang sama?
Diketahui : a(t) = 4t-5, v(0) =10 m/s
Ditanya : jarak pada t=3 detik ?
Jawab :
Langkah pertama, mari mengintegralkan percepatan.
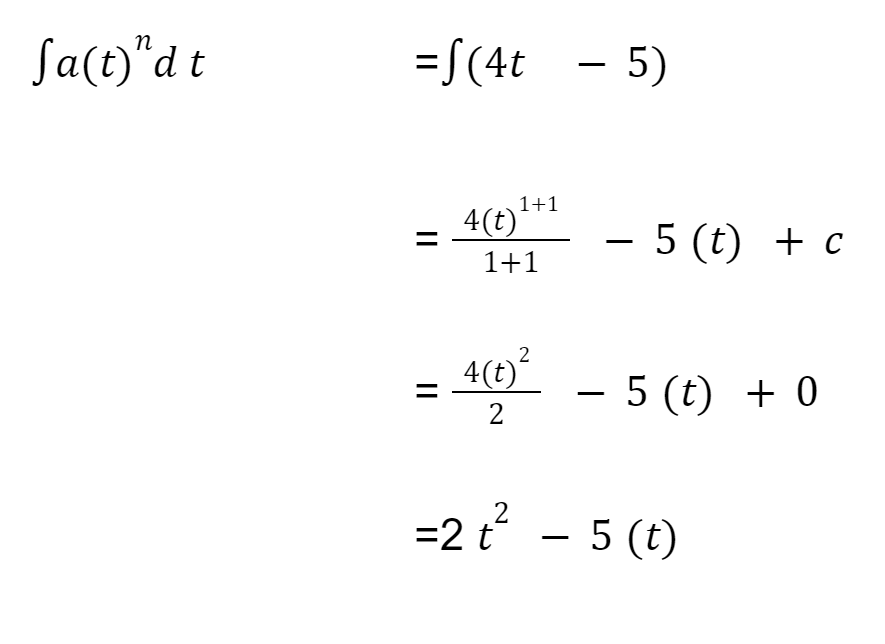
Lalu mencari kecepatan pada saat (t)
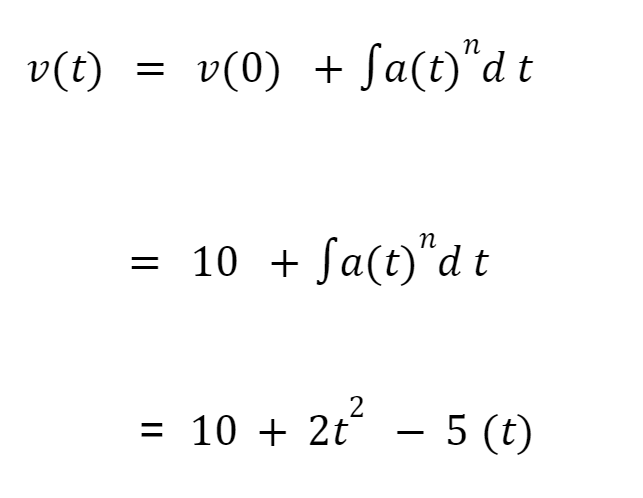
Kemudian mencari kecepatan pada saat (t=3)
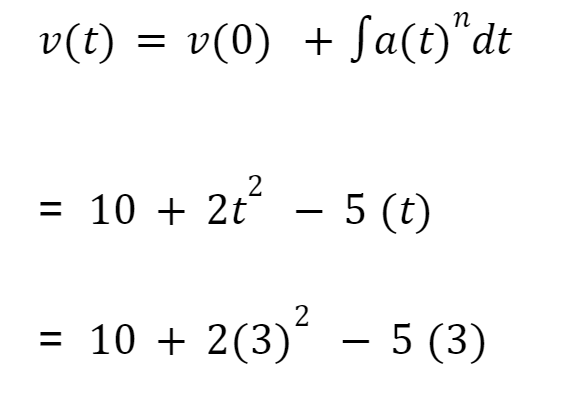
= 10+18-15 = 13 m/s
Maka kecepatan untuk t=3, hasilnya adalah 13 meter/sekon
Bagaimana mudah, bukan? Jika masih susah, untuk menambah pemahaman kamu tentang materi ini, silahkan simak beberapa contoh soal integral tak tentu di bawah ini ya!
5 Contoh Soal Integral Tak Tentu

Pada kesempatan kali ini, mari kita mempelajari integral tak tentu dengan melihat 5 contoh soal berikut ini. Jadi simak dengan baik – baik ya!
Contoh Soal 1

Jawab:
Kamu ingat mengenai sifat polinomial? Mari pakai rumus tersebut
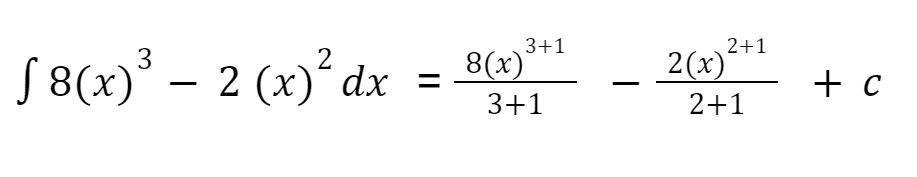
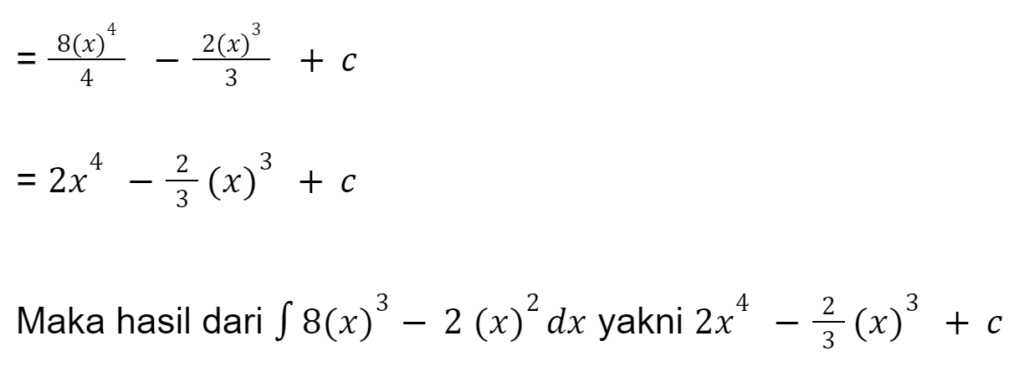
Contoh Soal 2
Yuk, selesaikan integral dari persamaan di bawah ini!

Contoh Soal 3
Selesaikan persamaan dari sifat logaritma integral tak tentu berikut ini !
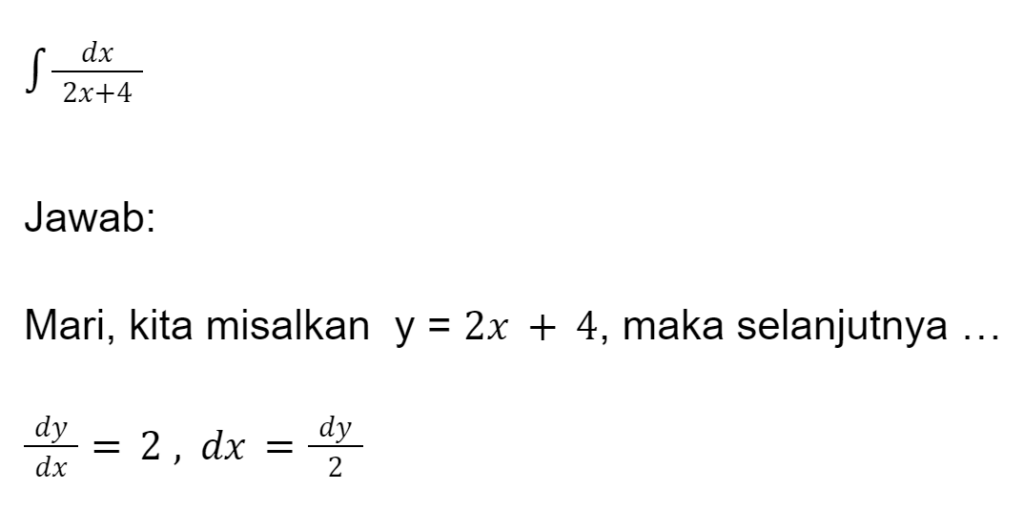

Contoh Soal 4
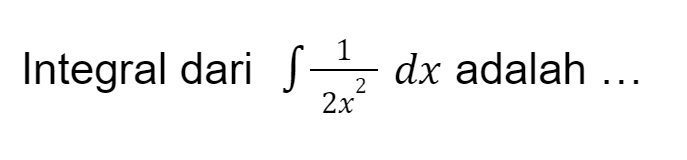
Jawab:
Masih ingat cara menaikkan pecahan dalam pangkat bukan? Ya, mari kita ubah terlebih dahulu persamaan diatas dengan bentuk pangkat.
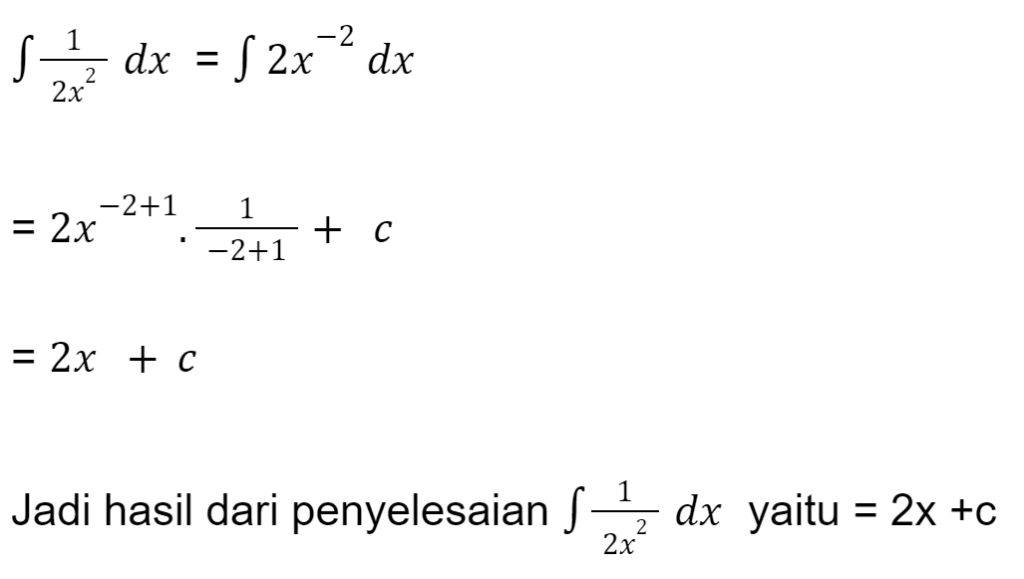
Contoh Soal 5
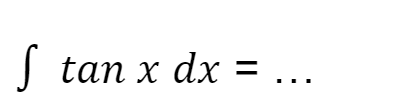
Jawab:
Untuk soal ini, kamu akan menggunakan kaidah logaritma jadi perlu memisalkan persamaan diatas. Sebelum masuk ke integral, pasti kamu tahu bukan trigonometri? Ya, kita ubah dulu tan x agar dapat kita integralkan.
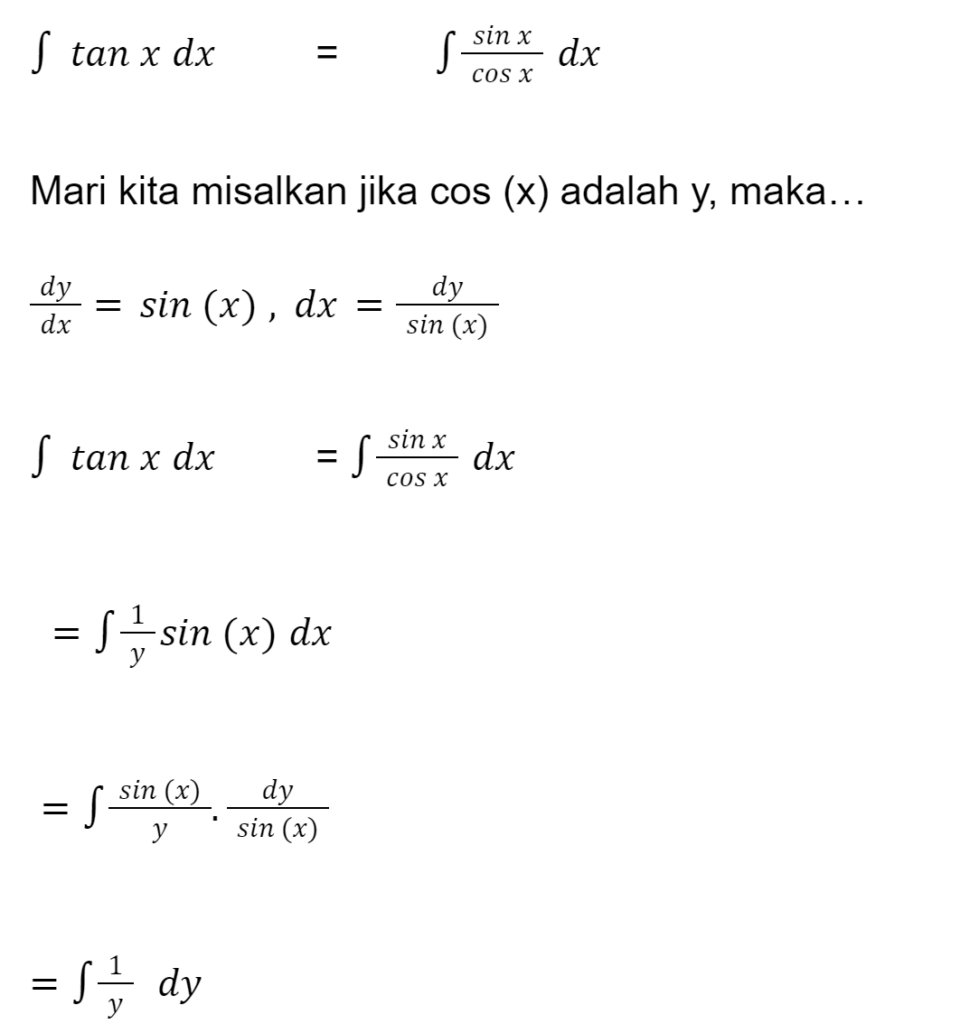
Nah, sama seperti contoh soal no.3 kita dapat mengubah 1/y dy ke bentuk logaritma

Kamu Sudah Pelajari Contoh Soal Integral Tak Tentu?
Dari penjelasan diatas, apakah kamu sudah paham dengan contoh soal integral tak tentu? Semoga artikel ini dapat membantu kamu dalam mempelajari bab integral tak tentu. Dengan demikian, kamu bisa mengerjakan soal-soal integral tak tentu secara tepat dan benar.