Dalam era teknologi informasi yang semakin maju, pemahaman tentang algoritma menjadi sangat penting. Algoritma adalah serangkaian langkah-langkah terstruktur yang digunakan untuk memecahkan masalah atau menyelesaikan tugas secara efisien.
Dalam artikel ini, kami akan membahas secara komprehensif tentang konsep algoritma, meliputi pengertian, sejarahnya, berbagai jenis yang umum digunakan, rumus-rumus terkait, dan memberikan beberapa contoh soal untuk menguji pemahaman Anda.
Mari kita mulai menjelajahi dunia algoritma yang menarik ini dan meningkatkan pemahaman kita bersama-sama.
Pengertian Algoritma
Algoritma merupakan serangkaian langkah terorganisasi yang dirancang untuk menyelesaikan sebuah masalah atau mencapai tujuan tertentu dengan efisien.
Algoritma atau teknik prosedur merupakan panduan atau rencana yang terdiri dari instruksi-instruksi yang jelas dan terurut secara logis. Tujuan dari teknik prosedur ini untuk menghasilkan hasil yang akurat, konsisten, dan dapat diandalkan.
Dalam konteks pemrograman dan komputasi, algoritma adalah langkah-langkah yang diterjemahkan ke dalam instruksi yang dapat dipahami oleh komputer.
Algoritma ini digunakan untuk memecahkan berbagai masalah, seperti pengolahan data, pengambilan keputusan, pencarian informasi, pengurutan data, dan banyak lagi.
Algoritma harus memenuhi beberapa karakteristik utama. Pertama, harus jelas dan terstruktur, sehingga setiap langkahnya dapat dipahami dengan jelas dan diikuti secara sistematis.
Kedua, teknik prosedur harus dapat menyelesaikan masalah dalam jumlah waktu yang wajar, tanpa memerlukan waktu yang tak terhingga. Ketiga, ia juga harus menghasilkan hasil yang benar dan konsisten setiap kali diterapkan pada masalah yang sama.
Penting untuk memahami bahwa teknik prosedur bukan hanya terkait dengan pemrograman komputer. Prinsip dan konsep istilah ini dapat diterapkan dalam berbagai bidang, seperti matematika, ilmu pengetahuan, bisnis, dan kehidupan sehari-hari.
Algoritma membantu kita dalam merumuskan langkah-langkah efektif untuk menyelesaikan masalah dan mencapai tujuan, baik secara manual maupun menggunakan bantuan komputer.
Sejarah
Sejarah algoritma memiliki akar yang sangat panjang dan bermula sejak zaman kuno. Konsep dasar ini juga telah ada sejak manusia mulai mengembangkan metode untuk memecahkan masalah dan menjalankan tugas-tugas tertentu secara sistematis.
Peradaban Mesir Kuno
Salah satu peradaban awal yang memberikan kontribusi besar dalam pengembangan algoritma adalah peradaban Mesir kuno. Mereka mengembangkan metode matematika untuk menghitung dan mengukur luas lahan, membangun piramida, dan merencanakan tata letak bangunan.
Mesir kuno juga memiliki sistem penulisan hieroglif yang kompleks, yang dapat dianggap sebagai suatu bentuk teknik prosedur untuk menyampaikan informasi secara terstruktur.
Peradaban Yunani Kuno
Selanjutnya, peradaban Yunani Kuno juga berperan penting dalam perkembangan algoritma. Matematikawan terkenal seperti Euclid dan Pythagoras mengembangkan metode-metode matematika yang menggunakan teknik ini.
Contohnya adalah algoritma Euclidean untuk menghitung FPB (Faktor Persekutuan Terbesar) dan algoritma Pythagoras untuk menghitung panjang sisi dalam segitiga siku-siku.
Abad Ke-9 dan Peran Islam
Pada abad ke-9, dunia Islam memberikan kontribusi besar dalam bidang matematika dan algoritma. Matematikawan seperti Al-Khawarizmi, yang dianggap sebagai bapak aljabar, mengembangkan metode yang disebut “Hisab al-Jabr wa al-Muqabala” (kalkulasi melalui pemulihan dan penyeimbangan).
Kontribusi ini menjadi dasar perkembangan algoritma matematika yang lebih lanjut di dunia barat.
Abad Ke-17
Pada abad ke-17, algoritma semakin berkembang dengan ditemukannya mesin hitung oleh Blaise Pascal dan Gottfried Wilhelm Leibniz. Setelah itu, Charles Babbage mengembangkan mesin analitik yang dianggap sebagai leluhur komputer modern pada abad ke-19.
Pada masa itu, teknik ini menjadi semakin penting dalam pemrograman dan komputasi.
Mulai Abad Ke-20
Seiring dengan perkembangan teknologi komputer pada abad ke-20, algoritma semakin kompleks dan canggih.
Konsep-konsep seperti pengurutan, pencarian, optimisasi, dan kecerdasan buatan semakin berkembang dan diterapkan dalam berbagai bidang, seperti ilmu komputer, sains data, kecerdasan buatan, dan sebagainya.
Sejarah teknik prosedur ini pun terus berkembang sejalan dengan perkembangan teknologi dan kebutuhan manusia.
Algoritma yang kita kenal saat ini merupakan hasil dari upaya kolaboratif dari banyak ilmuwan, matematikawan, dan ahli komputer di seluruh dunia. Mereka berkontribusi dalam memahami, merancang, dan menerapkan metode serta langkah-langkah yang efektif untuk memecahkan masalah dan mencapai tujuan.
Mengapa Algoritma Penting?
Lalu, pada bagian ini, kita akan membahas alasan mengapa algoritma memiliki peran yang sangat penting dalam dunia komputasi dan pemrograman. Berikut adalah penjelasan yang lebih rinci mengenai mengapa istilah ini sangat penting:
1. Efisiensi dan Kecepatan
Algoritma yang efisien memungkinkan eksekusi tugas dan pemrosesan data yang lebih cepat. Dalam dunia modern yang serba cepat, kecepatan eksekusi menjadi faktor kritis dalam mengatasi volume data yang besar dan kompleks.
Teknik yang baik juga dapat mengurangi kompleksitas waktu dan ruang yang diperlukan untuk menyelesaikan tugas tertentu, sehingga meningkatkan efisiensi dan kecepatan pemrosesan.
2. Pemecahan Masalah
Algoritma membantu dalam pemecahan masalah secara sistematis. Dengan mengembangkan teknik prosedur yang tepat, kita dapat merancang langkah-langkah logis untuk menyelesaikan masalah yang kompleks menjadi serangkaian sub masalah yang lebih kecil dan lebih mudah dipecahkan.
Teknik ini juga memungkinkan pendekatan yang terstruktur dan terorganisir dalam menghadapi berbagai masalah, baik dalam ilmu komputer, matematika, ilmu pengetahuan, dan bidang lainnya.
3. Pengembangan Aplikasi dan Software
Teknik prosedur ini adalah pondasi dari pengembangan aplikasi dan software. Ketika merancang aplikasi atau software, teknik yang tepat digunakan untuk mengatur logika, alur kerja, dan pemrosesan data.
Dengan teknik yang baik, aplikasi dapat berfungsi dengan baik, memberikan hasil yang diharapkan, dan memiliki kinerja yang optimal.
Algoritma juga memainkan peran penting dalam mengoptimalkan penggunaan sumber daya, seperti memori, CPU, dan jaringan, sehingga aplikasi dapat berjalan dengan efisien dan responsif.
4. Pengembangan Logika Berpikir
Studi teknik prosedur membantu dalam pengembangan logika berpikir dan pemecahan masalah. Melalui pemahaman tentang teknik prosedur dan proses pemrograman, seseorang dapat melatih pikiran analitis, pemecahan masalah, dan kemampuan berpikir logis.
Ini berdampak positif pada pengembangan keterampilan kognitif dan pemikiran abstrak yang penting dalam berbagai bidang kehidupan.
5. Inovasi dan Pengembangan Teknologi
Algoritma memainkan peran penting dalam inovasi dan pengembangan teknologi baru. Ketika merancang teknologi baru, teknik prosedur dikembangkan untuk memecahkan masalah khusus dan mencapai tujuan tertentu.
Misalnya, dalam bidang kecerdasan buatan (Artificial Intelligence), algoritma pembelajaran mesin (Machine Learning) dan algoritma jaringan saraf (Neural Networks) digunakan untuk mengenali pola, memprediksi, dan mengambil keputusan berdasarkan data yang diberikan.
6. Optimalisasi dan Pengambilan Keputusan
Algoritma digunakan untuk mengoptimalkan proses dan pengambilan keputusan. Ia pun digunakan untuk optimasi dan mencari solusi terbaik dari banyak kemungkinan solusi.
Dalam konteks ini, ia digunakan untuk mengidentifikasi kombinasi variabel atau parameter yang memberikan hasil optimal atau mendekati hasil optimal dalam situasi yang kompleks.
Ia juga dapat digunakan dalam pengambilan keputusan dengan mempertimbangkan berbagai faktor dan kriteria untuk mencapai keputusan yang terbaik.
7. Keamanan dan Kriptografi
Algoritma kriptografi digunakan untuk melindungi data dan informasi sensitif dari akses yang tidak sah. Algoritma enkripsi dan dekripsi yang kuat memastikan kerahasiaan dan integritas data yang ditransmisikan atau disimpan.
Keberadaan teknik kriptografi yang handal dan aman penting dalam menjaga privasi dan keamanan komunikasi elektronik, transaksi keuangan, dan data pribadi.
8. Pengembangan Kreativitas
Algoritma dapat digunakan untuk memfasilitasi pengembangan kreativitas dalam berbagai bidang, seperti seni, musik, dan desain.
9. Reusabilitas
Istilah ini pun berguna dalam penggunaan ulang berbagai konteks dan aplikasi yang serupa. Algoritma yang telah terbukti berhasil dapat digunakan ulang dalam pengembangan sistem baru atau untuk menyelesaikan masalah yang serupa.
10. Replikasi dan Skalabilitas
Istilah ini memainkan peran penting dalam replikasi dan skalabilitas sistem. Dalam pengembangan sistem yang memerlukan replikasi, ia digunakan untuk mendistribusikan dan mengelola beban kerja di antara beberapa entitas atau node.
Ia juga digunakan untuk merancang sistem yang dapat dengan mudah diskalakan sesuai dengan peningkatan jumlah pengguna atau data.
Jenis-jenis Algoritma
Ada banyak jenis algoritma yang digunakan dalam banyak bidang. Jenis-jenisnya tergantung pada jenis masalah yang ingin diselesaikan dan cara pendekatannya. Berikut ini adalah beberapa jenisnya yang umum digunakan:
1. Algoritma Pencarian
Algoritma pencarian digunakan untuk menemukan suatu elemen atau informasi tertentu dalam kumpulan data. Beberapa jenis ini yang umum adalah pencarian linier, pencarian biner, dan pencarian hashing.
Pencarian linier mencari elemen satu per satu secara berurutan, sedangkan pencarian biner memanfaatkan sifat data terurut untuk mencari elemen dengan membagi-bagi data menjadi setengah bagian. Lalu pencarian hashing menggunakan fungsi hash untuk mengindeks dan mencari data secara efisien.
2. Algoritma Berurutan (Sequential)
Jenis algoritma ini merupakan satu yang paling sederhana. Langkah-langkahnya dieksekusi secara berurutan, satu per satu, tanpa adanya perulangan atau percabangan. Selain itu, ini cocok digunakan untuk tugas sederhana yang membutuhkan langkah-langkah yang jelas dan tidak kompleks.
Jenis ini digunakan untuk mengurutkan kumpulan data secara teratur, baik secara menaik (ascending) maupun menurun (descending). Beberapa jenis pengurutan yang umum adalah pengurutan gelembung, pengurutan seleksi, pengurutan penyisipan, pengurutan penggabungan, dan pengurutan cepat.
Setiap jenis berurutan memiliki cara kerja dan kompleksitas yang berbeda, yang dapat dipilih berdasarkan kebutuhan dan jumlah data yang akan diurutkan.
3. Algoritma Percabangan
Ini menggunakan kondisi atau percabangan logika untuk memutuskan langkah-langkah selanjutnya. Dalam percabangan, langkah-langkah yang diambil bergantung pada hasil evaluasi kondisi tertentu.
Contohnya adalah IF-ELSE yang menjalankan langkah-langkah tertentu jika suatu kondisi terpenuhi dan langkah-langkah lain jika kondisi tersebut tidak terpenuhi.
4. Algoritma Perulangan
Jenis perulangan digunakan ketika suatu langkah atau sekelompok langkah harus diulang beberapa kali. Ini memungkinkan eksekusi yang berulang berdasarkan kondisi atau sejumlah iterasi yang telah ditentukan.
Selain itu, perulangan memungkinkan pengulangan tugas-tugas tertentu dengan efisien tanpa perlu menulis langkah-langkah yang sama secara berulang.
5. Algoritma Rekursif
Jenis rekursif adalah jenis algoritma yang memanggil dirinya sendiri untuk memecahkan masalah yang lebih kecil. Pada setiap pemanggilan rekursif, masalah dipecahkan menjadi versi yang lebih kecil hingga mencapai kasus dasar yang dapat diselesaikan langsung.
Rekursif ini umumnya digunakan untuk masalah yang dapat dipisahkan menjadi submasalah yang lebih sederhana.
6. Algoritma Graf
Graf digunakan untuk membuat model dan memecahkan masalah yang melibatkan struktur data atau hubungan dan keterhubungan antar objek dalam bentuk graf. Jenis graf sangat penting dalam pemecahan masalah yang melibatkan jaringan, perencanaan rute, pemodelan sosial, dan sebagainya.
Beberapa jenis graf yang umum adalah pencarian lintas graf (traversal), pencarian jarak terpendek (shortest path), jembatan terhubung terkecil (minimum spanning tree), dan aliran maksimum (maximum flow).
Beberapa algoritma graf yang umum digunakan adalah Depth-First Search (DFS) dan Breadth-First Search (BFS) untuk traversal graf. Selain itu, teknik Dijkstra untuk mencari jalur terpendek, dan Bellman-Ford untuk mencari jalur terpendek dengan bobot negatif.
Ditambah lagi, terdapat juga teknik prosedur Prim dan Kruskal untuk mencari pohon lintasan terpendek dalam graf berbobot.
7. Algoritma Divide and Conquer
Divide and Conquer adalah pendekatan pemecahan masalah yang melibatkan pemecahan masalah menjadi submasalah yang lebih kecil, memecahkan sub masalah secara rekursif, dan menggabungkan solusi submasalah untuk mendapatkan solusi akhir.
Contoh Divide and Conquer adalah pengurutan cepat (Quick Sort) dan pencarian biner (Binary Search).
8. Algoritma Backtracking
Backtracking digunakan ketika mencari solusi dari suatu masalah dengan melakukan percobaan secara berulang dengan mengubah keputusan yang diambil pada setiap langkah.
Jika pada suatu langkah tidak ditemukan solusi yang memenuhi syarat, maka pengaturannya akan kembali ke langkah sebelumnya dan mencoba opsi lain. Contoh backtracking adalah Eight Queens Problem yang mencari solusi penempatan delapan ratu di papan catur tanpa saling serang.
9. Algoritma Greedy
Greedy adalah algoritma yang memilih langkah terbaik pada setiap langkahnya dengan harapan akan mencapai solusi optimal secara keseluruhan. Pada setiap langkah, jenis ini akan membuat keputusan lokal terbaik tanpa mempertimbangkan konsekuensi jangka panjang.
Contoh jenis ini adalah Kruskal untuk mencari pohon lintasan terpendek dalam graf berbobot minimum.
10. Algoritma Dynamic Programming
Dynamic Programming adalah pendekatan pemecahan masalah yang memecahkan masalah secara bertahap dengan memecahkannya menjadi submasalah yang lebih kecil dan menyimpan solusi submasalah tersebut untuk menghindari perhitungan berulang.
Jenis ini efektif untuk masalah yang memiliki sifat overlapping subproblems. Contoh jenis ini adalah Fibonacci dan Knapsack.
11. Algoritma Pengurutan
Teknik pengurutan digunakan untuk mengurutkan elemen-elemen dalam suatu kumpulan data. Ada berbagai metode pengurutan yang tersedia, termasuk pengurutan gelembung, pengurutan penyisipan, pengurutan seleksi, dan pengurutan cepat.
Setiap metode pengurutan memiliki pendekatan yang berbeda untuk memindahkan dan membandingkan elemen-elemen dalam kumpulan data sehingga tersusun dengan benar.
12. Algoritma Pencarian
Teknik pencarian digunakan untuk mencari elemen tertentu dalam kumpulan data.
Ada beberapa metode pencarian yang umum digunakan, seperti pencarian linear (sequential) yang mencari secara berurutan dari awal hingga ditemukan atau pencarian biner yang membagi kumpulan data menjadi dua bagian dan mencari di setengah bagian yang relevan.
Setiap jenis memiliki pendekatan dan prinsip kerja yang berbeda-beda. Pemilihan jenis yang tepat tergantung pada sifat masalah yang akan diselesaikan dan ketersediaan sumber daya yang ada.
Dalam prakteknya, seringkali digunakan kombinasi dari beberapa jenis algoritma untuk memecahkan masalah yang kompleks.
Rumus atau Formula dan Langkah Analisis
Harap diingat bahwa teknik prosedur lebih fokus pada langkah-langkah dan logika dalam menyelesaikan masalah daripada rumus matematika yang khas. Namun, konsep-konsep dan notasi di bawah ini dapat membantu dalam menganalisis dan memahami kompleksitas algoritma secara lebih mendalam.
Berikut adalah beberapa contohnya:
1. Notasi Big O
Notasi Big O digunakan untuk menggambarkan kompleksitas waktu atau ruang dari suatu algoritma. Biasanya dinyatakan sebagai O(f(n)), di mana f(n) adalah fungsi yang menggambarkan pertumbuhan waktu atau ruang teknik prosedur seiring dengan pertambahan ukuran input (n).
Misalnya, O(n) menunjukkan kompleksitas linear, O(n^2) menunjukkan kompleksitas kuadratik, dan seterusnya. Jadi, jika ukuran inputnya berlipat ganda, kompleksitas waktu algoritma akan meningkat menjadi empat kali lipat.
2. Rumus Pengurangan (Subtraction Formula)
Rumus ini digunakan dalam analisis mengurangi kompleksitas algoritma yang lebih kompleks menjadi bagian-bagian yang lebih kecil. Dalam rumus ini, kompleksitas total dihitung sebagai jumlah kompleksitas dari setiap bagian yang saling terkait.
Misalkan, sebuah algoritma memiliki tiga bagian yang saling terkait dengan kompleksitas waktu masing-masing O(n), O(n^2), dan O(log n). Total kompleksitasnya dapat dihitung dengan menjumlahkan kompleksitas masing-masing bagian, yaitu O(n) + O(n^2) + O(log n).
3. Rumus Perkalian (Multiplication Formula)
Rumus ini digunakan ketika algoritma melibatkan pengulangan atau iterasi. Dalam rumus ini, kompleksitasnya dihitung sebagai perkalian kompleksitas setiap iterasi dengan jumlah total iterasi yang dilakukan.
Jika sebuah algoritma memiliki loop atau pengulangan dengan kompleksitas waktu O(n) dan jumlah iterasi sebanyak m, kompleksitas total algoritma dapat dihitung dengan mengalikan kompleksitas per iterasi dengan jumlah total iterasi, yaitu O(n) * m.
Contohnya jika matriks A berukuran m x n dan matriks B berukuran n x p, maka algoritma ini memiliki kompleksitas waktu O(mnp).
Kemudian, langkah algoritmanya yaitu dengan iterasi sebanyak m untuk baris matriks A, iterasi sebanyak p untuk kolom matriks B, lalu iterasi sebanyak n untuk mengalikan elemen-elemen matriks A dan B.
4. Rumus Rekursi (Recursion Formula)
Rumus ini digunakan dalam analisis algoritma yang melibatkan rekursi, yaitu ketika algoritma memanggil dirinya sendiri. Rumus ini memungkinkan penghitungan kompleksitas rekursif berdasarkan jumlah panggilan rekursif yang terjadi dan kompleksitas algoritma pada setiap panggilan.
Misalkan sebuah algoritma rekursif memanggil dirinya sendiri sebanyak k kali, dan kompleksitas pada setiap panggilan adalah O(f(n)). Kompleksitas rekursif tersebut dapat dihitung dengan rumus O(k * f(n)).
Contoh kasusnya yaitu, “Jika n adalah bilangan bulat positif, algoritma ini memiliki kompleksitas waktu O(n).”
Maka, langkah tulisannyanya yaitu:
- Jika n = 0, kembalikan 1.
- Jika n > 0, kembalikan n dikali dengan faktorial dari n-1.
Contoh Soal
Selanjutnya, diberikan beberapa contoh soal untuk membantu Anda memahami konsep dari materi ini. Lanjutkan membaca!
1. Contoh Soal 1
Data yang diberikan berupa angka tanggal (hari, bulan, tahun). Buatlah algoritma untuk menentukan zodiak berdasarkan tanggal kelahiran.
Jawaban:
Contoh penulisan algoritmanya adalah sebagai berikut:

2. Contoh Soal 2
Data yang diberikan berupa bilangan bulat positif. Buatlah algoritma untuk menentukan apakah bilangan tersebut merupakan bilangan Armstrong atau bukan. Bilangan Armstrong adalah bilangan yang jumlah dari pangkat setiap digitnya sama dengan bilangan itu sendiri.
Jawaban:
Contoh penulisannya adalah sebagai berikut:

3. Contoh Soal 3
Data yang diberikan berupa bilangan bulat. Buatlah algoritma untuk menentukan apakah bilangan tersebut merupakan bilangan prima atau bukan.
Jawaban:
Contoh penulisan algoritmanya adalah sebagai berikut:

4. Contoh Soal 4
Data yang diberikan berupa suatu kalimat. Buatlah algoritma untuk menghitung jumlah kata dalam kalimat tersebut. Anggap bahwa kata-kata dipisahkan oleh spasi.
Jawaban:
Contoh penulisan algoritmanya adalah sebagai berikut:

5. Contoh Soal 5
Data yang diberikan berupa angka bilangan bulat. Jika angka tersebut merupakan bilangan positif, maka tampilkan “Bilangan positif”. Jika angka tersebut merupakan bilangan negatif, maka tampilkan “Bilangan negatif”. Jika angka tersebut adalah nol, maka tampilkan “Nol”.
Jawaban:
Contoh penulisan algoritmanya adalah seperti berikut ini:
Algoritma:
1. Baca angka.
2. Jika angka > 0, maka:
– Tampilkan “Bilangan positif”.
3. Jika angka < 0, maka:
– Tampilkan “Bilangan negatif”.
4. Jika angka = 0, maka:
– Tampilkan “Nol”.

6. Contoh Soal 6
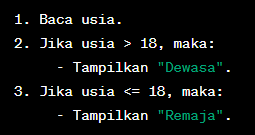
Data yang diberikan berupa usia seseorang. Jika usia lebih dari 18 tahun, maka tampilkan “Dewasa”. Jika usia kurang dari atau sama dengan 18 tahun, maka tampilkan “Remaja”.
Jawaban:
Contoh penulisan algoritmanya adalah seperti berikut ini:
Algoritma:
1. Baca usia.
2. Jika usia > 18, maka:
– Tampilkan “Dewasa”.
3. Jika usia <= 18, maka:
– Tampilkan “Remaja”.
7. Contoh Soal 7
Data yang diberikan berupa nilai ujian siswa. Jika nilai ujian lebih besar atau sama dengan 70, maka siswa dinyatakan lulus. Jika nilai ujian kurang dari 70, maka siswa dinyatakan tidak lulus.
Jawaban:
Contoh penulisan algoritmanya adalah seperti berikut ini:
Algoritma:
1. Baca nilai ujian.
2. Jika nilai >= 70, maka:
– Tampilkan “Lulus”.
3. Jika nilai < 70, maka:
– Tampilkan “Tidak lulus”.

8. Contoh Soal 8
Data yang diberikan berupa bilangan bulat. Jika bilangan tersebut merupakan bilangan positif genap, maka tampilkan “Bilangan positif genap”. Jika bilangan tersebut merupakan bilangan positif ganjil, maka tampilkan “Bilangan positif ganjil”.
Namun, jika bilangan tersebut adalah nol, maka tampilkan “Nol”. Jika bilangan tersebut merupakan bilangan negatif genap, maka tampilkan “Bilangan negatif genap”. Lalu jika bilangan tersebut merupakan bilangan negatif ganjil, maka tampilkan “Bilangan negatif ganjil”.
Jawaban:
Contoh penulisan algoritmanya adalah seperti berikut ini:
Algoritma:
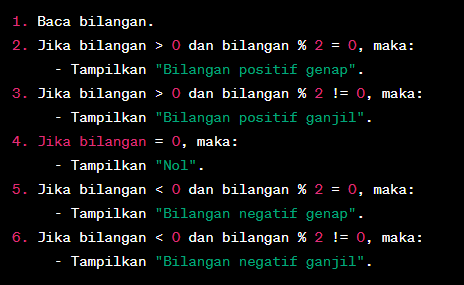
1. Baca bilangan.
2. Jika bilangan > 0 dan bilangan % 2 = 0, maka:
– Tampilkan “Bilangan positif genap”.
3. Jika bilangan > 0 dan bilangan % 2 != 0, maka:
– Tampilkan “Bilangan positif ganjil”.
4. Jika bilangan = 0, maka:
– Tampilkan “Nol”.
5. Jika bilangan < 0 dan bilangan % 2 = 0, maka:
– Tampilkan “Bilangan negatif genap”.
6. Jika bilangan < 0 dan bilangan % 2 != 0, maka:
– Tampilkan “Bilangan negatif ganjil”.
9. Contoh Soal 9
Data yang diberikan berupa bilangan bulat positif. Jika bilangan tersebut merupakan bilangan prima, maka tampilkan “Bilangan prima”. Jika bukan bilangan prima, maka tampilkan “Bukan bilangan prima”.
Jawaban:
Contoh penulisan algoritmanya adalah seperti berikut ini:
Algoritma:
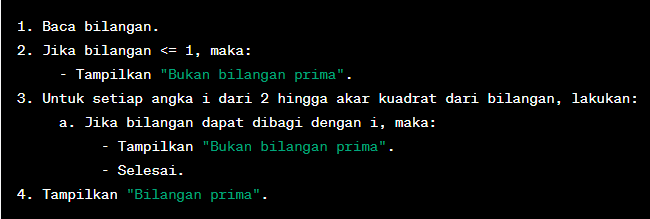
1. Baca bilangan.
2. Jika bilangan <= 1, maka:
– Tampilkan “Bukan bilangan prima”.
3. Untuk setiap angka i dari 2 hingga akar kuadrat dari bilangan, lakukan:
a. Jika bilangan dapat dibagi dengan i, maka:
– Tampilkan “Bukan bilangan prima”.
– Selesai.
4. Tampilkan “Bilangan prima”.
10. Contoh Soal 10
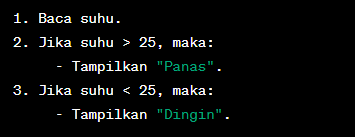
Data yang diberikan berupa suhu dalam derajat Celcius. Jika suhu lebih dari 25 derajat, maka tampilkan “Panas”. Jika suhu kurang dari 25 derajat, maka tampilkan “Dingin”.
Jawaban:
Contoh penulisan algoritmanya adalah seperti berikut ini:
Algoritma:
1. Baca suhu.
2. Jika suhu > 25, maka:
– Tampilkan “Panas”.
3. Jika suhu < 25, maka:
– Tampilkan “Dingin”.
Sudah Paham Mengenai Algoritma?
Dalam artikel ini, kami telah mengupas tuntas mengenai algoritma. Dengan pemahaman tentang sejarah, pengertian, jenis, rumus, dan contoh soalnya, diharapkan Anda dapat lebih memahami konsep dan penerapannya dalam berbagai situasi. Semoga artikel ini bermanfaat bagi Anda dalam mempelajari dan memahami algoritma. Teruslah berlatih dan eksplorasi lebih jauh untuk meningkatkan pemahaman Anda tentang algoritma dan penerapannya dalam berbagai bidang.

