Pada dasarnya, momen inersia merupakan salah satu konsep fundamental dalam fisika yang berkaitan dengan gerak rotasi benda. Konsep ini memiliki peran penting dalam memahami bagaimana benda berputar di sekitar sumbu tertentu. Semakin tinggi inersia benda, maka akan semakin tahan terhadap rotasi sudut.
Pengertian
Inersia rotasi atau massa sudut dapat dikenal sebagai nama lain dari momen inersia. Terdefinisi dengan ukuran ketahanan suatu benda terhadap perubahan gerak rotasinya. Hal tersebut, bergantung pada massa benda terhadap sumbu rotasi.
Dalam hal ini, massa benda yang jauh dari sumbu rotasi akan memiliki kontribusi inersia rotasi yang lebih besar daripada massa yang lebih dekat dengan sumbu rotasi. Ketika massa bergerak lebih jauh dari sumbu rotasi, maka akan menjadi semakin sulit untuk mengubah kecepatan rotasi sistem.
Secara naluriah, hal ini karena massa akan membawa lebih banyak momentum bersamanya di sekitar lingkaran atau karena kecepatan yang lebih tinggi dan karena vektor momentum berubah lebih cepat. Kedua efek ini tergantung pada jarak dari sumbu.
Simbol dalam inersia rotasi berupa (I). Satuan Sistem Internasional atau SI dalam momen ini adalah kgm². Satuan ini mewakili massa (dalam kilogram) dan kuadrat jarak (dalam meter) dari sumbu rotasi. Sedangkan dalam satuan British berupa lbf.ft.s².
Konsep inersia rotasi sangat penting dalam mekanika rotasi dan digunakan untuk menganalisis gerakan rotasi benda, seperti roda berputar, mesin berputar, dan sistem lain yang melibatkan dinamika rotasi.
Penting juga untuk menggambarkan dan menganalisis sistem rotasi secara akurat. Baik dalam aplikasi teoritis dan praktis. Para insinyur, fisikawan, dan ilmuwan di berbagai disiplin ilmu mengandalkannya untuk melakukan perhitungan, merancang mesin, memprediksi stabilitas, dan memecahkan masalah rotasi yang kompleks.
Rumus Inersia Rotasi
Rumus umum untuk inersia rotasi adalah sebagai berikut:
I = ∫ r² dm
Sehingga, setelah melakukan pengintegralan, maka rumus menjadi:
I = mr²
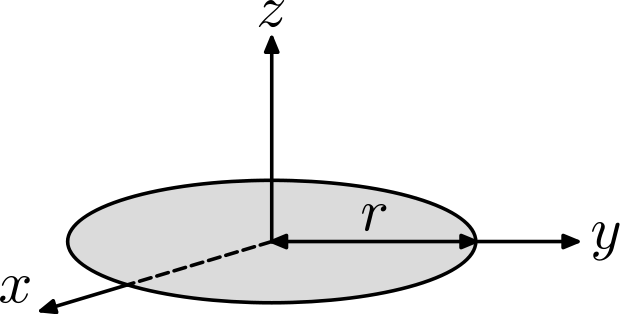
Dalam rumus tersebut, I melambangkan momen inersia, m adalah massa yang diukur dalam kilogram (kg), dan r adalah jarak tegak lurus terhadap sumbu rotasi yang diukur dalam meter (m).
Momen ini memiliki rumus yang berbeda, tergantung pada bentuk dan sumbu rotasi untuk objek tertentu, seperti silinder, bola, dan geometri yang lebih kompleks. Rumus-rumus ini diturunkan dengan menerapkan prinsip-prinsip kalkulus dan geometri untuk distribusi massa objek.
Dari Mana Datangnya Momen Inersia?
Hukum Newton menyatakan bahwa percepatan linier suatu benda berbanding lurus dengan gaya yang bekerja ketika massa konstan. Kita dapat menyatakan hal ini dengan persamaan di bawah ini, di mana Ft adalah gaya, m adalah massa benda, dan at adalah percepatan translasi.
Ft= m x at
Demikian pula, penggunaan torsi untuk gerakan rotasi, hal ini sama dengan gaya rotasi dan jarak tegak lurus terhadap sumbu rotasi. Namun, untuk percepatan translasi pada gerakan rotasi sama dengan percepatan sudut (α) dan jari-jari r.
αt = r . α T/r = m . r² . α
Sehingga, nilai torsi menjadi:
T = m . r² . α
T = I . α
Inersia rotasi adalah kebalikan dari massa dalam hukum kedua Newton untuk percepatan linier, tetapi diterapkan pada percepatan sudut.
Hukum kedua Newton menggambarkan nilai torsi yang bekerja pada benda, dimana berbanding lurus dengan momen massa inersia benda dan percepatan sudutnya. Seperti yang terlihat pada derivasi di atas, torsi T sama dengan momen inersia (I) dan percepatan sudut (α).
Momen Inersia dalam Berbagai Bentuk
Untuk lebih memahami konsep, mari kita lihat beberapa contoh dalam berbagai bentuk. Terdapat 3 bentuk yang umum pada keseharian kita, yaitu:
1. Bola
Bola adalah salah satu contoh sederhana yang dapat digunakan untuk menggambarkannya. Inersia rotasi sebuah bola yang homogen dapat dihitung menggunakan rumus:
I = (2/5) . m . r²
Dalam rumus tersebut, m adalah massa bola dan r adalah jari-jari bola. Jika jari-jari bola diperbesar, nilai inersia juga akan meningkat.
2. Tabung
Tabung berbentuk silinder juga merupakan contoh yang berguna dalam memahami inersia rotasi. Momen inersia tabung yang homogen sekitar sumbu sejajar dengan sumbu panjangnya adalah:
I = (1/2) . m. r²
Dalam rumus tersebut, m adalah massa tabung dan r adalah jari-jari tabung. Jika massa tabung diperbesar, inersia juga akan meningkat.
3. Benda yang Kompleks
Benda yang lebih kompleks, seperti segitiga atau benda dengan bentuk yang tidak beraturan, memiliki nilai massa sudut yang lebih sulit untuk dihitung secara langsung menggunakan rumus umum.
Untuk benda-benda semacam itu, massa sudut dapat dihitung melalui metode integral dengan membagi benda menjadi elemen massa yang lebih kecil.
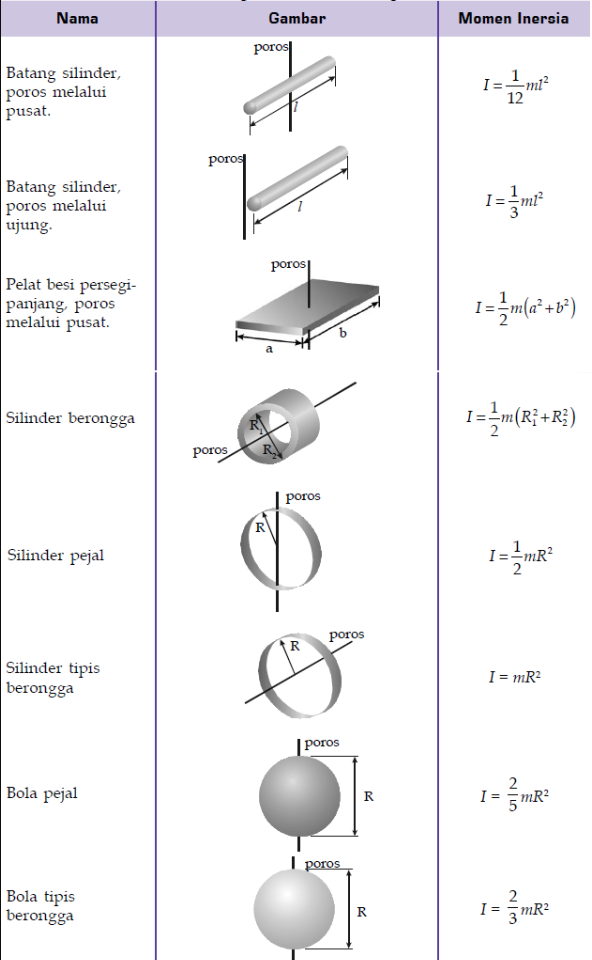
Selain pada benda-benda yang memiliki bentuk yang ada pada umumnya, dalam benda kompleks, menghitung inersia rotasi juga perlu memperhatikan dari mana poros benda tersebut. Berikut dapat Anda lihat rumus detailnya pada setiap bentuk pada gambar:
Contoh Soal Momen Inersia
Berikut beberapa contoh soal dan jawabannya untuk menambah pemahaman kamu:
1. Soal Pertama
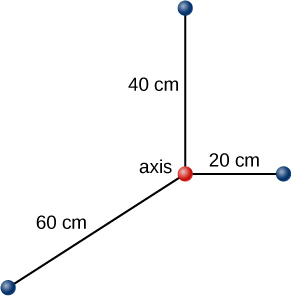
Sistem partikel ditunjukkan pada gambar berikut. Setiap partikel memiliki massa 0,3 kg dan mereka semua terletak di bidang yang sama. Berapa momen inersia pada sumbu yang diberikan?
Jawaban:
Massa semua partikel sama. Oleh karena itu, m = 0,3 kg.
I = Σ m . r²= 0,3 kg . [(0,6 m)² + (0,4 m)² + (0,2 m)²] = 0,168 kg m²
2. Soal Kedua
Sebuah silinder memiliki panjang sebesar 0,7 m dan memiliki massa sebesar 50 kg, tentukanlah momen inersia dari silinder tersebut, apabila poros melalui pusat!
Jawaban:
Menghitung silinder pada poros melalui pusat adalah:
I = 1/12 . m . L²= 1/12 . 50 kg . (0,7 m)²= 2,0417 kg m²
3. Soal Ketiga
Seorang atlet duduk di kursi berputar sambil memegang beban latihan 10 kg di masing-masing tangan. Kapan atlet akan lebih mungkin untuk berputar, ketika dia mengulurkan tangannya jauh dari tubuhnya atau ketika dia menarik lengannya dekat dengan tubuhnya?
Jawaban:
Ketika atlet mengulurkan tangannya, momen inersia meningkat ketika jarak antara berat dan sumbu rotasinya meningkat. Ketika atlet menarik lengannya, jarak antara bobot dan sumbu rotasi berkurang, dan begitu juga momen inersianya.
Oleh karena itu, atlet lebih cenderung berputar ketika ia menarik tangannya, karena inersia rotasinya akan lebih kecil dan tubuh akan memiliki lebih sedikit resistensi atau ketahanan untuk berputar.
Penerapan Massa Sudut
Massa sudut memiliki berbagai penerapan penting dalam kehidupan sehari-hari dan ilmu pengetahuan. Berikut adalah beberapa penerapan inersia rotasi yang umum:
1. Olahraga dan Seni Pertunjukan
Momen inersia digunakan dalam banyak olahraga dan seni pertunjukan yang melibatkan gerakan rotasi. Contohnya termasuk loncatan dengan bantuan tali, atraksi sirkus seperti gerakan lingkaran dengan alat-alat tertentu, atau bahkan gerakan dalam seni bela diri seperti putaran pada tae kwon do.
2. Mesin dan Alat Berat
Dalam industri dan manufaktur, sering digunakan dalam perancangan mesin dan alat berat. Pemahaman massa sudut yang tepat, memungkinkan para insinyur untuk mengoptimalkan performa mesin, mengurangi getaran dan keausan yang tidak diinginkan, serta meningkatkan efisiensi operasi.
3. Kendaraan dan Transportasi
Momen ini juga sangat relevan dalam perancangan kendaraan dan transportasi. Misalnya, inersia rotasi adalah faktor kunci dalam perhitungan kestabilan kendaraan saat berbelok atau berakselerasi. Memahaminya, membantu insinyur dalam merancang sistem suspensi dan sistem pengendalian yang efektif.
Memahami konsep inersia sangat penting dalam berbagai bidang, termasuk fisika dan teknik, bahkan kehidupan sehari-hari. Fakta ini memungkinkan kita untuk menganalisa dan memprediksi gerakan rotasi objek, merancang sistem mekanis yang efisien, dan menentukan stabilitas struktur dan kendaraan.
Bagaimana Pemahaman Momen Inersia Kamu saat Ini?
Momen inersia adalah konsep penting dalam fisika yang berkaitan dengan gerak rotasi benda. Konsep ini digunakan untuk mengukur ketahanan suatu benda terhadap perubahan gerak rotasinya.
Dengan memahami inersia rotasi, kita dapat menggambarkan dan memprediksi gerakan rotasi benda dengan lebih baik. Inersia rotasi memiliki rumus yang terkait dengan distribusi massa benda terhadap sumbu rotasi, serta berbagai contoh dan penerapan dalam kehidupan sehari-hari.
Dengan pengetahuan tentang konsep inersia, kita dapat mengaplikasikan prinsip ini dalam berbagai bidang, mulai dari olahraga hingga industri dan transportasi.