Modulus Elastisitas: Pengertian, Besaran, Rumus, dan Contoh Soalnya

Apakah Anda pernah bertanya-tanya mengapa sebuah benda dapat mengalami deformasi saat memiliki beban, namun kemudian kembali ke bentuk semula setelah beban tersebut dihilangkan? Fenomena ini dapat Anda pahami dengan konsep modulus elastisitas atau juga sering dikenal sebagai modulus Young. 

Jadi dalam artikel ini, kita akan menggali lebih dalam tentang modulus elastisitas, termasuk besaran dan rumusnya. Tidak hanya itu, kami juga akan menyajikan contoh soal dan pembahasannya untuk membantu Anda dalam memahami konsep ini dengan lebih baik.

Pengertian Modulus Elastisitas

Modulus elastisitas adalah besaran mekanik yang mengukur sejauh mana suatu material dapat mengalami deformasi elastis ketika memiliki tegangan. Konsep ini pertama kali dikenalkan oleh seorang fisikawan Inggris bernama Thomas Young pada awal abad 19.

Sementara arti dari deformasi elastis adalah suatu bentuk deformasi sementara yang terjadi pada material saat mendapat tegangan. Namun, material akan kembali ke bentuk semula setelah tegangan dihilangkan.

Sehingga, konsep fisika ini juga sering disebut dengan naman modulus Young. Modulus Young sering berguna untuk menggambarkan sifat mekanik material, terutama material padat seperti logam, beton, kayu, dan sebagainya.

Berbagai Komponen Besaran dalam Modulus Elastisitas

Modulus elastisitas biasanya dilambangkan dengan huruf “E” yang mana juga memiliki beberapa komponen penting yang harus Anda pahami. Antara lain:

1. Tegangan (σ) 

Tegangan adalah gaya yang bekerja pada suatu material per satuan luas. Dalam konsep elastisitas, tegangan pada material disebut sebagai tegangan elastis yang mana menyebabkan deformasi elastis pada material.

2. Regangan (ε) 

Sementara regangan adalah perubahan dimensi material akibat terkena tegangan. Untuk menghitungnya, Anda dapat dengan membagi perubahan dimensi material dengan dimensi aslinya. Regangan yang terjadi bersifat elastis, artinya material akan kembali ke dimensi aslinya setelah tegangan dihilangkan.

3. Tegangan Batas Elastis (σy) 

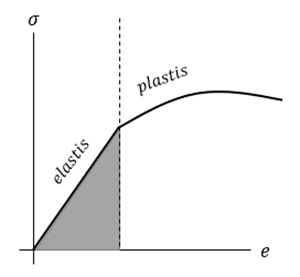
Terakhir, tegangan batas elastis adalah tegangan maksimum yang dapat dikenakan pada suatu material tanpa menyebabkan deformasi permanen atau plastis. Maka, di atas tegangan batas elastis, material akan mengalami deformasi plastis dan tidak akan kembali ke bentuk semula setelah tegangan dihilangkan.

Satuan Modulus Elastisitas

Modulus Young memiliki satuan pascal (Pa) atau Newton per meter persegi (N/m²). Pascal adalah satuan internasional yang berguna untuk mengukur tekanan dan tegangan pada material. 

Satuan pascal dapat ditulis dalam bentuk yang lebih besar atau lebih kecil, seperti kilopascal (kPa) atau megapascal (MPa). Tergantung pada besarnya nilai modulus Young yang diukur. Satuan pascal (Pa) ekuivalen dengan: 

• 1 Pa = 1 N/m² 
• 1 kPa = 1000 N/m² 
• 1 MPa = 1.000.000 N/m²

Dimensi Modulus Elastisitas

Secara matematis, dimensi modulus Young adalah [M1L-1T-2], yang mana menunjukkan bahwa modulus Young memiliki dimensi massa per satuan panjang per satuan waktu kuadrat. Dalam notasi fisika, M adalah massa, L adalah panjang, dan T adalah waktu. 

Sehingga, dimensi ini mencerminkan sifat mekanik material dan sejauh mana suatu material dapat menahan tegangan dan deformasi elastis.

Rumus Modulus Elastisitas dan Masing-masing Besarannya

Modulus elastisitas dapat Anda hitung menggunakan beberapa rumus, tergantung pada besaran yang diketahui. Berikut ini adalah rumus untuk berbagai besarannya:

1. Rumus Modulus Elastisitas (E) 

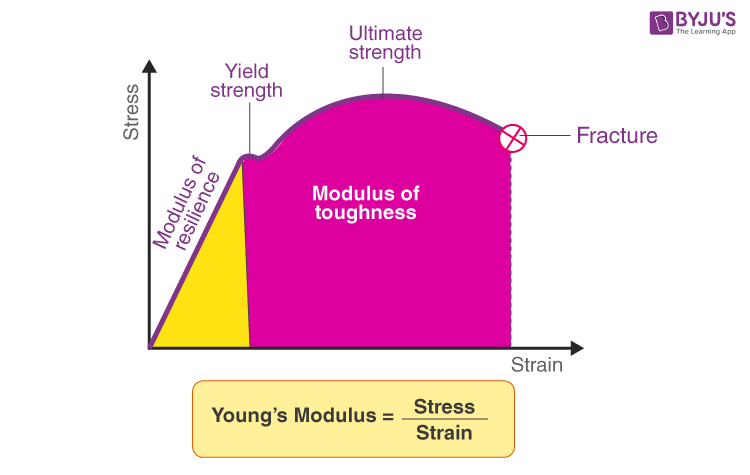
Modulus elastisitas atau modulus Young dapat Anda hitung dengan membagi tegangan elastis (σ) dengan regangan elastis (ε): 

E = σ / ε

Di bawah ini disediakan Tabel yang menunjukkan berbagai nilai modulus Young (E) untuk beberapa material yang umum digunakan dalam berbagai aplikasi teknik dan konstruksi. 

Nilai modulus Young adalah indikator penting dalam mengevaluasi sifat mekanik material, seperti kekuatan, kekakuan, dan elastisitasnya. Semakin tinggi nilai modulus Young, maka semakin kaku dan kaku material tersebut.

Berikut adalah tabel beberapa nilai modulus Young (E) untuk beberapa material yang umum digunakan:

Material	Modulus Young (E) (GPa)
Aluminium	70-80
Baja	200-220
Tembaga	100-130
Beton	30-50
Kayu (tergantung jenis)	10-20
Kaca	70-85
Titanium	100-120
Stainless Steel	190-230
Karet	0.01-0.1
Logam Tungsten	400

Catatan: Nilai-nilai dalam tabel dapat berbeda-beda tergantung pada sifat dan komposisi material.

Memahami nilai modulus elastisitas dari berbagai material membantu insinyur dan perancang dalam memilih material yang tepat untuk berbagai aplikasi teknik. 

Misalnya, untuk struktur yang memerlukan kekakuan tinggi, logam seperti baja atau titanium bisa menjadi pilihan yang baik. Sedangkan untuk aplikasi elastis seperti bantalan karet, modulus Young yang lebih rendah akan lebih diinginkan.

2. Rumus Tegangan Elastis (σ) 

Tegangan elastis dapat Anda hitung dengan mengalikan modulus elastisitas (E) dengan regangan elastis (ε): 

σ = E * ε atau σ = F / A

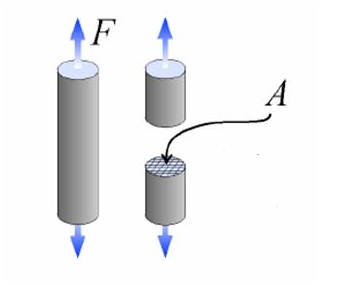
Keterangan:

• F = gaya yang bekerja pada balok (N) 
• A = luas penampang melintang balok (m²)

3. Rumus Regangan Elastis (ε) 

Sementara regangan elastis dapat Anda hitung dengan rumus: 

ε = σ / E atau ε = ΔL / L

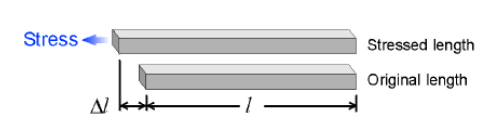
Keterangan:

• ΔL = perubahan panjang batang (m) 
• L = panjang batang sebelum diberikan gaya tarik (m)

Contoh Soal Tentang Modulus Elastisitas dan Pembahasannya

Simak 3 contoh soal di bawah ini untuk mempelajari lebih dalam mengenai rumus-rumus dalam meteri modulus elastisitas:

1. Contoh Soal 1

Sebuah batang logam dengan modulus elastisitas 2 x 10¹¹ Pa mengalami regangan elastis sebesar 0,001. Berapakah tegangan elastis yang bekerja pada batang logam tersebut?

Pembahasan: 

Diketahui: 

Modulus elastisitas (E) = 2 x 10¹¹ Pa 

Regangan elastis (ε) = 0,001

Maka, kita akan menggunakan rumus tegangan elastis: σ = E * ε

Substitusi nilai yang diberikan: 

σ = 2 x 10^11 Pa * 0,001 

σ = 2 x 10⁸ Pa

Jadi, tegangan elastis yang bekerja pada batang logam tersebut adalah 2 x 10⁸ Pascal.

2. Contoh Soal 2 

Sebuah balok baja memiliki panjang 2 meter dan penampang melintang 0,01 meter persegi. Jika balok tersebut mengalami regangan elastis sebesar 0,002 dan gaya yang diberikan pada balok adalah 20N, maka hitunglah nilai E!

Pembahasan: 

Diketahui:

• Panjang balok (L) = 2 meter 
• Luas penampang (A) = 0,01 m²
• Regangan elastis (ε) = 0,002
• Gaya yang bekerja pada balok (F) = 20 N

Untuk menghitung nilai E atau modulus Young, kita dapat menggunakan rumus:

E = σ / ε

Di mana: 

E = modulus Young

(Pa) σ = tegangan elastis 

(Pa) ε = regangan elastis

Langkah 1: Hitung tegangan elastis (σ)

Pertama-tama, kita perlu mencari nilai tegangan elastis (σ) untuk menggantikan nilainya dalam rumus modulus elastisitas.

Kita dapat menghitung tegangan elastis menggunakan rumus:

σ = F / A

Kemudian substitusi nilai yang diberikan: 

σ = F / A

σ = 20 N / 0,01 m² = 2000 N/m²

Langkah 2: Hitung modulus elastisitas (E)

Kita dapat menghitung E menggunakan rumus: 

E = σ / ε

Lalu substitusi nilai yang diberikan: 

E = 2000 N/m² / 0,002 

E = 1.000.000 N/m²

Jadi, modulus Young (E) dari balok baja tersebut adalah 1.000.000 N/m² atau 1 MPa (megapascal).

3. Contoh Soal 3

Sebuah batang baja dengan panjang 3 meter dan penampang melintang 0,02 meter persegi diberikan gaya tarik sebesar 5000 N. Sebelumnya, batang tersebut berada dalam kondisi tanpa regangan. Hitunglah regangan elastis yang dialami oleh batang baja tersebut.

Pembahasan:

Diketahui: 

Panjang batang (L) = 3 m 

Luas penampang melintang batang (A) = 0,02 m² 

Gaya tarik yang bekerja pada batang (F) = 5000 N

Pertama, regangan elastis dapat dihitung menggunakan rumus: 

ε = ΔL / L

Karena batang awalnya berada dalam kondisi tanpa regangan, maka ΔL adalah panjang yang terjadi akibat gaya tarik. Dalam hal ini, ΔL adalah hasil gaya tarik yang bekerja pada batang.

Substitusi nilai yang diberikan: 

ε = ΔL / L

ε = 3 m (perubahan panjang) / 3 m (panjang awal) = 0,001 atau 0,1%

Penerapan Modulus Elastisitas dalam Kehidupan Sehari-hari

Modulus Young memiliki berbagai penerapan dalam kehidupan sehari-hari dan dunia teknik. Beberapa contoh penerapannya adalah:

1. Industri Konstruksi 

Pada bidang ini, modulus elastisitas berguna untuk menghitung daya dukung material dalam konstruksi gedung, jembatan, dan infrastruktur lainnya. Misalnya, material dengan nilai E yang tinggi sering bermanfaat dalam konstruksi untuk menjamin stabilitas dan ketahanan struktur.

2. Industri Otomotif 

Sedangkan dalam industri otomotif, penggunaannya adalah untuk merancang dan menguji material pada bagian-bagian mobil dan kendaraan lainnya. Material dengan nilai E yang tepat dapat mengurangi risiko deformasi atau kerusakan saat kendaraan bergerak atau mengalami benturan.

3. Industri Elektronik 

Selain itu, modulus Young juga berguna dalam desain dan manufaktur komponen elektronik seperti chip mikro dan baterai. Material dengan modulus elastisitas yang tepat membantu melindungi komponen elektronik dari tekanan dan perubahan suhu.

4. Pembuatan Alat Musik 

Sementara dalam pembuatan alat musik, modulus Young material pada senar atau bagian-bagian lainnya mempengaruhi kualitas suara yang dihasilkan. Alasannya, material dengan nilai E yang tepat memberikan resonansi dan kualitas suara yang baik.

5. Pengembangan Material Baru 

Studi ini membantu dalam pengembangan material baru dengan sifat mekanik yang unggul, seperti material komposit dan material superkonduktor.

Sudah Paham Mengenai Modulus Elastisitas? 

Berdasarkan penjelasan di atas, maka kita menjadi paham bahwa modulus elastisitas memiliki peran yang sangat penting dalam memahami sifat mekanik material. Sehingga, dapat berguna dalam berbagai bidang seperti konstruksi, otomotif, elektronik, dan industri lainnya. 

Dengan pemahaman yang baik tentang materi ini, kita dapat merancang dan memilih material yang tepat untuk berbagai aplikasi yang beragam dalam kehidupan sehari-hari.