Pasti kamu sudah tak asing lagi dengan istilah bangun ruang yang merupakan salah satu materi pelajaran matematika di sekolah. Materi tersebut tidak hanya ada saat masih mengenyam bangku Sekolah Dasar, namun juga pada jenjang selanjutnya.
Pada dasarnya, bangun ruang memiliki berbagai macam bentuk dan kegunaan yang beragam. Dengan bentuk yang sedemikian rupa, benda tersebut memiliki sifat khasnya masing-masing.
Pada artikel ini, kamu akan belajar mengenai macam-macam serta pembahasan soal mengenai benda-benda tersebut. Situasi ini perlu kamu perhatikan karena secara sifat, benda-benda tersebut memiliki besaran volume yang berbeda.
Apa Itu Bangun Ruang?
Secara garis besar, pengertian dari bangun ruang adalah sebuah benda yang terdapat sisi, titik sudut, hingga bidang diagonal. Oleh karena itu, hanya benda tersebut yang memiliki sifat unik sebagai benda tiga dimensi.
Suatu benda dapat dikatakan sebagai bangun ruang apabila memiliki bagian-bagian berikut ini:
- Sisi.
- Rusuk.
- Titik sudut.
- Diagonal ruang.
- Diagonal sisi.
- Bidang diagonal.
Macam-Macam Bangun Ruang
Berikut ini macam-macam bangun ruang beserta rumusnya yang perlu kamu pahami:
1. Kubus
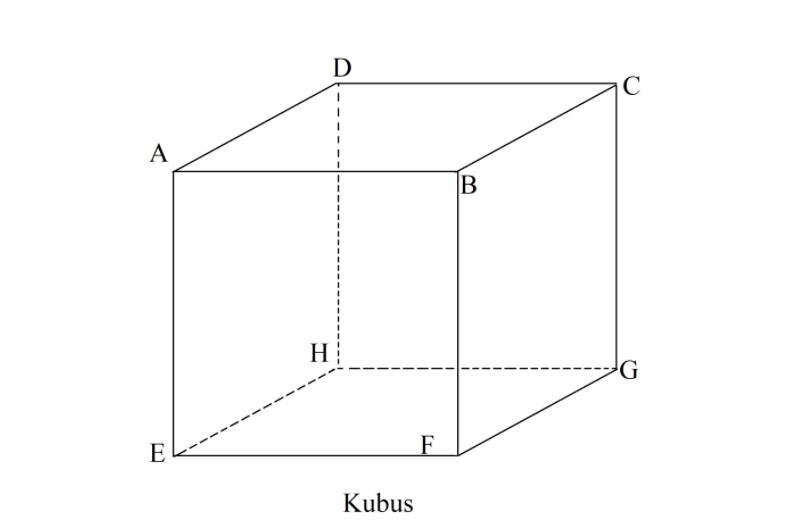
Benda bervolume satu ini ternyata masuk dalam kategori prisma dengan besar sisi yang selalu sejajar dan sama. Banyak sekali benda di sekitar kamu yang berbentuk kubus, termasuk rubik.
Di bawah ini merupakan rumus dari kubus:
| Luas Permukaan | L = 6 × (s × s) |
| Volume | V = s × s × s |
2. Balok
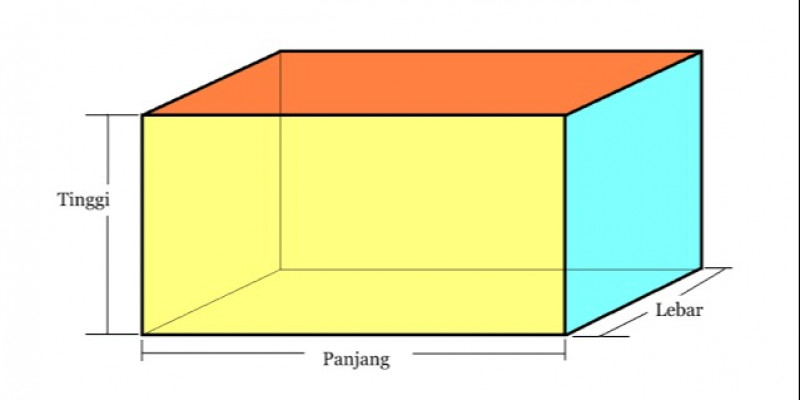
Sekilas, karakteristik benda bervolume satu ini hampir sama dengan kubus dan memiliki 8 titik sudut. Namun, balok memiliki sistem perhitungan yang berbeda karena panjang balok lebih dari kubus.
Berikut ini merupakan rumus dari balok:
| Luas Permukaan | L = 2 × {(p × l) + (p × t) + (l × t)} |
| Volume | V = p × l × t |
Baca Juga : Memahami Ciri-ciri Balok, Rumus, dan Contoh Soal
3. Prisma
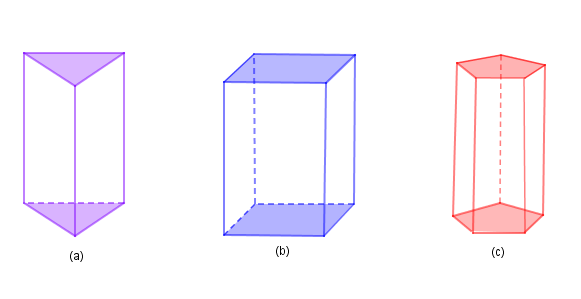
Selanjutnya adalah keluarga prisma. Kenapa jenis bangun ruang ini disebut sebagai keluarga prisma? Karena pada umumnya, prisma terbagi menjadi beberapa bagian, yaitu balok, kubus, prisma segi lima, prisma segi enam, dan seterusnya.
Ciri utama dari prisma adalah adanya dua bidang sejajar yaitu alas dan atap yang membatasi ruang benda tersebut. Lalu, bidang tegak akan berpotongan dengan rusuk sejajar. Ada juga tinggi prisma yang dapat kamu hitung dengan menggunakan jarak atap dan alas.
Oleh sebab itu, rumus prisma dapat berbeda menyesuaikan dengan banyak sisi benda tersebut. Berikut ini adalah rumus untuk prisma:
| Luas Permukaan | L = 2 × luas alas + luas selimut |
| Volume | V = luas alas × t |
4. Limas
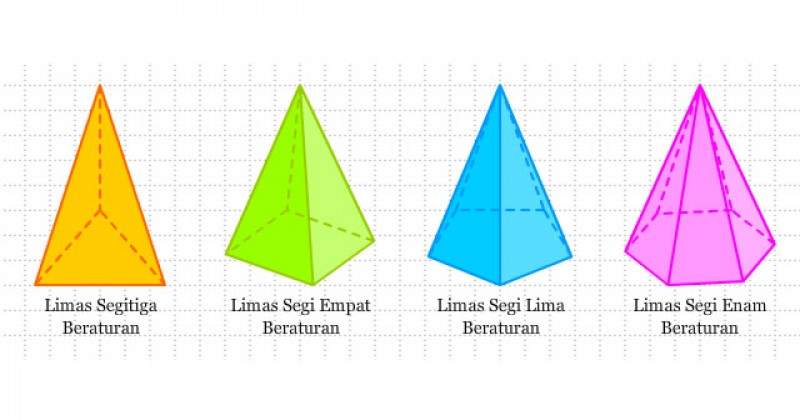
Selanjutnya, sebuah bangun ruang dengan alas berbentuk segi-n dan memiliki sisi selimut berbentuk segitiga dengan titik pusat yang terdapat pada luar bidang. Banyak orang menyebut benda bervolume satu ini dengan sebutan limas.
Sama halnya dengan prisma, limas memiliki berbagai jenis yang menyesuaikan dengan jumlah sisi pada alasnya. Berikut adalah rumus untuk limas:
| Luas Permukaan | L = luas alas + luas selimut |
| Volume | V = ⅓ × luas alas × t |
5. Tabung
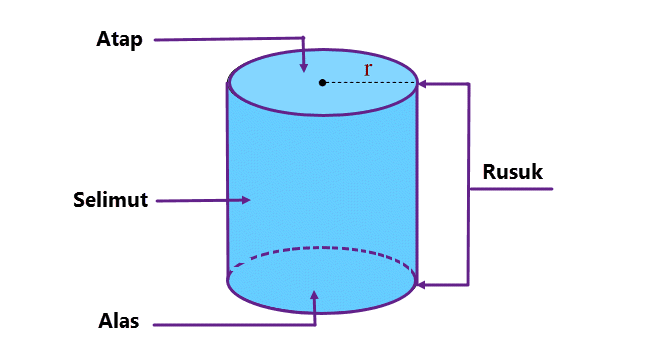
Tabung merupakan salah satu jenis dari bangun ruang yang memiliki sisi berbentuk lengkungan. Selain itu, alas dan atap benda bervolume satu ini berbentuk lingkaran atau oval, sehingga selimut yang menyelimuti bidang bentuknya melengkung. Dengan ciri memiliki atap dan alas, benda ini juga termasuk dalam prisma lingkaran.
Berikut adalah rumus untuk tabung:
| Luas Permukaan | L = 2π × r × t × 2π × r2 |
| Volume | V = π × r2 × t |
6. Kerucut
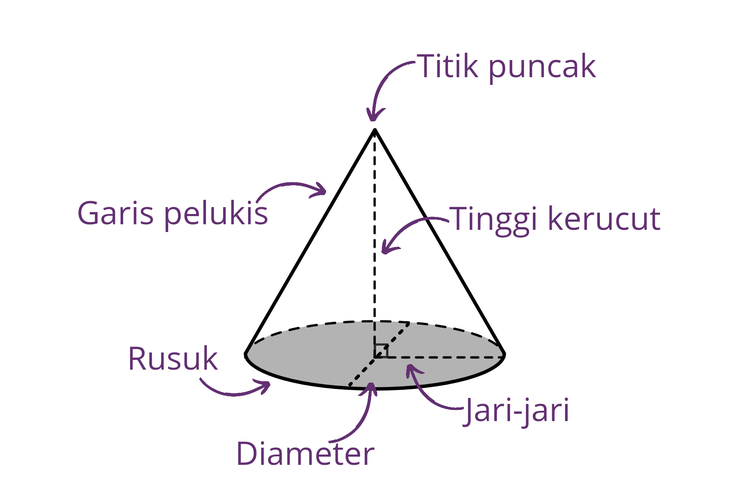
Selanjutnya, benda bervolume yang bernama kerucut memiliki alas berbentuk lingkaran seperti tabung, namun tidak memiliki atap. Selain itu, bentuk selimut dari kerucut juga melengkung dan mengerucut di bagian atas, sehingga bangun ruang ini memiliki titik sudut pada atas sisi ruang.
| Luas Permukaan | L = π × r × (r + s) |
| Volume | V = ⅓ × π × r × r × t |
7. Bola
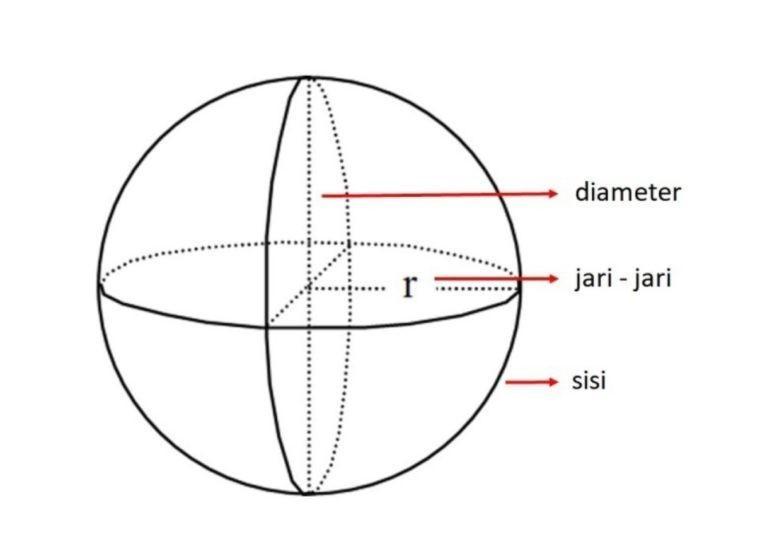
Bola merupakan salah satu benda bervolume yang paling sering kamu temui pada lingkungan sekitar. Benda bervolume ini secara khusus tidak memiliki atap ataupun alas, hanya berselimutkan bidang lengkung layaknya tabung dan kerucut.
Berikut adalah rumus untuk bola:
| Luas Permukaan | L = 4 × π × r2 |
| Volume | V = 4/3 × π × r3 |
Baca Juga : Rumus Bola (Luas, Keliling, Volume), Contoh, dan Pembahasan
Sifat Bangun Ruang
Sesuai dengan jenisnya, bangun ruang mempunyai sifat masing-masing. Lantas, seperti apa sifat dari benda bervolume tersebut?
1. Kubus
Walaupun sudah sangat umum untuk mengetahui sifat dari kubus yang pastinya memiliki sisi yang sama, berikut ini adalah sifat lengkap dari kubus:
- Memiliki 4 buah diagonal ruang.
- Terdapat 12 diagonal bidang.
- Adanya 6 bidang sisi sama besar berbentuk persegi.
- Mempunyai 8 titik sudut siku-siku.
- Memiliki 12 rusuk sama panjang.
2. Balok
Di samping itu, sifat dari balok kurang lebih sama dengan kubus karena kedua benda tersebut memiliki bentuk yang hampir sama.
- Mempunyai 4 buah diagonal ruang.
- Ada 12 buah diagonal bidang.
- 8 titik sudut berbentuk siku-siku.
- 6 dari 12 rusuknya saling berhadapan dan sama panjang.
- Terdapat 6 sisi persegi panjang.
3. Prisma
Selanjutnya, prisma yang memiliki bentuk cukup beragam sifat-sifatnya akan menyesuaikan dengan banyak sisi dari alas dan atapnya. Berikut ini sifat dari prisma:
- Terdapat 6 titik sudut.
- Rusuk berjumlah 9 buah.
- Bentuk jaring-jaring terdiri dari 2 segitiga dan 3 persegi panjang.
- Terdapat 5 bidang sisi dengan 2 sisi segitiga dan 3 sisi segi empat.
4. Limas
Sama halnya dengan kubus dan balok, bangun ruang limas juga memiliki sifat yang kurang lebih sama dengan prisma, yaitu:
- Jumlah titik sudut menyesuaikan dengan alas.
- Terdapat 1 titik sudut yang terletak pada puncak ruang.
- Bidang sisi berbentuk segitiga.
- Jumlah sisi alas beragam.
5. Tabung
Berikut ini adalah sifat-sifat tabung:
- Alas dan atap berbentuk lingkaran.
- Jarak antara alas dan tutup merupakan tinggi bidang.
- Jaring-jaring tabung terdiri dari 1 persegi dan 2 lingkaran.
- Selimut bidang berbentuk lengkungan.
6. Kerucut
Selanjutnya, berikut ini sifat dari kerucut:
- Hanya terdapat 1 titik sudut.
- Terdapat 1 rusuk sudut.
- 1 sisi alas berbentuk lingkaran dan 1 selimut yang mengerucut.
7. Bola
Sifat dari bangun ruang bola adalah sebagai berikut:
- Terdapat 1 sisi saja.
- Titik pusat hanya 1.
- Tidak memiliki titik sudut.
- Jari-jari bersifat tidak terhingga.
Contoh Soal dan Pembahasan
Agar kamu lebih memahami konsep dari bangun ruang dan penggunaan rumusnya, berikut ini adalah contoh pembahasan yang dapat kamu pelajari:
Soal 1
Terdapat balok yang memiliki ukuran 15 cm untuk panjangnya, lebar 10 cm, dan tingginya 7 cm. Hitunglah volume balok tersebut!
Pembahasan
Rumus volume balok adalah V = p × l × t.
P = 15 cm.
L = 10 cm.
T = 7 cm.
Jadi, V = 15 × 10 × 7 = 1.050 cm3.
Soal 2
Ada sebuah kerucut di dalam sebuah tabung hingga titik puncak kerucut menyentuh tutup tabung. Hitung perbandingan volume kedua bidang tersebut jika alasnya memiliki ukuran sama!
Pembahasan
Rumus dari volume kerucut adalah V = ⅓ × π × r2 × t dan untuk rumus volume tabung adalah V = π × r2 × t. Kamu hanya perlu mencoret persamaan yang sama, sehingga hasilnya adalah ⅓.
Soal 3
O merupakan titik puncak dari sebuah limas segi empat O.GHIJ yang memiliki volume 50 cm3. Diketahui juga bahwa bidang GHIJ merupakan persegi dengan tinggi 10 cm. Tentukan panjang dari GH!
Pembahasan
Rumus volume limas adalah V = ⅓ × luas alas × t, maka
V = ⅓ × luas alas × t
50 = ⅓ × GH2 × 10
GH2 = 3 × 50 / 10 = 15
GH = √15 = 3,9 cm.
Sudah Hafal Macam-macam Bangun Ruang dan Sifatnya?
Bangun ruang merupakan materi pelajaran yang sudah sangat umum bagi semua kalangan. Selain itu, benda-benda ini juga sering ada di lingkungan sekitar kamu.
Dengan memahami sifat dan rumus dari masing-masing bangun ruang tersebut, kamu juga akan lebih mudah mengaplikasikannya pada kehidupan sehari-hari, misal pada proses pembuatan wadah tabung, kotak simpan, aksesoris, dan sebagainya.

