Dalam ilmu matematika, bilangan bulat atau integer menjadi konsep dasar yang memainkan peran penting dalam pemecahan masalah matematika yang lebih kompleks. Pasalnya, bilangan ini mencakup angka tanpa pecahan yang mencakup bilangan positif, negatif, dan nol, membentuk urutan dari yang terkecil hingga terbesar.
Sebut saja bilangan positif 1, 2, 3, kemudian bilangan negatif seperti -1, -2, -3, dan nol adalah angka netral. Dalam artikel ini, Anda akan menjelajahi lebih lanjut tentang integer dan bagaimana menerapkannya dalam konteks matematika yang lebih luas.
Apa Itu Bilangan Bulat?
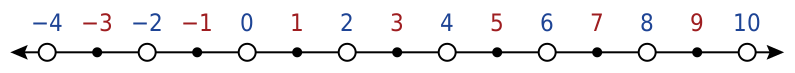
Bilangan bulat berasal dari kata Latin “integer” (diucapkan IN-tuh-jer) adalah bilangan bukan bilangan pecahan yang bisa bernilai positif, negatif, atau nol. Contoh integer adalah -5, 1, 5, 8, 97, dan 3,043.
Himpunan integer, yang dilambangkan dengan huruf Z, secara formal terdefinisikan sebagai berikut:
Z = (…, -3, -2, -1, 0, 1, 2, 3, 4, 5, …)
Dalam persamaan matematika, bilangan bulat yang tidak diketahui atau tidak ditentukan akan terwakili oleh huruf kecil yang dicetak miring dari “tengah akhir” alfabet. Simbol huruf yang paling umum adalah p, q, r, dan s.
Jenis Bilangan Bulat
Dalam kategori tertentu, integer terdiri dari beberapa jenis yang mana memiliki sifat-sifat khusus. Berikut adalah beberapa jenisnya yang umum:
1. Nol
Pada dasarnya, nol bukan termasuk bilangan bulat positif atau negatif. Nol adalah angka netral yang tidak memiliki tanda khusus, baik plus (+) atau minus (-).
2. Bilangan Bulat Positif
Integer positif adalah bilangan asli yang juga disebut bilangan hitung. Bilangan ini juga kadang-kadang dilambangkan dengan Z +. Secara teori, bilangan ini terletak di sisi kanan angka 0 pada garis bilangan. Mulai dari angka 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, dan seterusnya.
3. Bilangan Bulat Negatif
Integer negatif adalah nilai negatif dari bilangan asli. Bilangan ini dilambangkan dengan Z–. Secara teori, bilangan negatif terletak di sisi kiri angka 0 pada garis bilangan. Mulai dari -1, -2, -3, -4, -5, -6, -7, -8, -9, -10, dan seterusnya.
4. Bilangan Cacah
Bilangan cacah adalah kumpulan bilangan yang terdiri dari bilangan nol dan bilangan bulat positif, atau sering disebut sebagai bilangan non-negatif. Simbol bilangan cacah adalah W yang mana merupakan singkatan dari Whole Numbers. Contoh bilangan cacah meliputi 0, 1, 2, 3, 4, 5, dan seterusnya.
5. Bilangan Ganjil dan Genap
Bilangan ganjil adalah himpunan bilangan yang bukan kelipatan dua atau tidak habis terbagi 2. Sedangkan bilangan genap adalah himpunan bilangan kelipatan 2 atau habis terbagi 2. Misalnya, 8 adalah bilangan genap karena bisa habis apabila dibagi 2, sementara 13 adalah bilangan ganjil karena tidak habis terbagi 2.
6. Bilangan Prima
Bilangan prima adalah bilangan yang lebih besar dari 1 dan hanya dapat terbagi oleh 1 atau dirinya sendiri. Contoh bilangan prima termasuk 2, 3, 5, 7, 11, 13, dan seterusnya.
7. Bilangan Komposit
Bilangan komposit adalah bilangan yang lebih besar dari 1 dan bukan bilangan prima karena dapat terbagi oleh faktor lain selain 1 dan dirinya sendiri. Contoh bilangan komposit adalah 4 dan 6, karena keduanya dapat terbagi oleh faktor selain 1 dan dirinya sendiri.
Anda perlu ingat bahwa bilangan prima dan bilangan komposit juga dapat menjadi bilangan ganjil atau genap. Misalnya, bilangan 3 adalah bilangan prima dan ganjil, sedangkan bilangan 4 adalah bilangan komposit dan genap. Tetapi, bilangan ganjil tidak selalu merupakan bilangan prima.
Bagaimana Cara Mewakili Bilangan Bulat pada Garis Bilangan?
Seperti yang telah menjadi bahasan tiga kategori integer, Anda dapat dengan mudah mewakilinya pada garis bilangan berdasarkan bilangan bulat positif, negatif, dan nol.
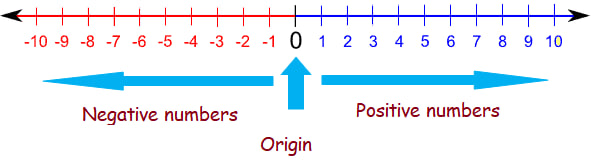
Nol adalah pusat bilangan bulat pada garis bilangan. Integer positif terletak di sisi kanan angka nol dan integer negatif terletak di sebelah kiri angka nol. Untuk lebih jelasnya, lihat gambar di bawah ini:
Operasi Aritmatika pada Bilangan Bulat
Operasi aritmatika pada bilangan bulat adalah langkah-langkah matematika dasar yang dilakukan pada bilangan tersebut untuk menghitung, menyelesaikan masalah, atau melakukan perhitungan lainnya. Berikut adalah beberapa operasi aritmatika utama yang dapat dilakukan:
1. Penambahan atau Penjumlahan
Saat menambahkan dua bilangan bulat dengan tanda yang sama, tambahkan nilai absolut, dan tuliskan jumlah dengan tanda yang disediakan dengan angka. Misalnya:
(+4) + (+7) = +11
(-6) + (-4) = -10
Sambil menambahkan dua bilangan dengan tanda berbeda, kurangi nilai absolut, dan tuliskan selisihnya dengan tanda angka yang memiliki nilai absolut terbesar. Misalnya:
(-4) + (+2) = -2
(+6) + (-4) = +2
2. Pengurangan
Saat mengurangkan dua bilangan, ubah tanda angka kedua yang sedang dikurangi, dan ikuti aturan penjumlahan. Misalnya:
(-7) – (+4) = (-7) + (-4) = -11
(+8) – (+3) = (+8) + (-3) = +5
3. Perkalian
Saat mengalikan dua integer atau bilangan bulat, aturannya cukup sederhana. Jika kedua integer memiliki tanda yang sama, maka hasilnya positif. Jika integer memiliki tanda yang berbeda, maka hasilnya negatif. Misalnya:
(+2) x (+3) = +6
(+3) x (-4) = – 12
4. Pembagian
Aturan untuk membagi integer mirip dengan perkalian. Jika kedua integer memiliki tanda yang sama, maka hasilnya positif. Jika bilangan memiliki tanda yang berbeda, maka hasilnya negatif. Demikian pula contohnya:
(+6) ÷ (+2) = +3
(-16) ÷ (+4) = -4
Cara Membandingkan Bilangan Bulat
Membandingkan integer berarti menentukan hubungan antara dua bilangan tersebut, apakah salah satu lebih besar, lebih kecil, atau sama dengan yang lain. Dalam proses perbandingan ini, Anda bisa menggunakan simbol-simbol berikut:
- Simbol “>” menunjukkan bahwa suatu bilangan lebih besar daripada yang lain.
- Simbol “<” mengindikasikan bahwa suatu bilangan lebih kecil daripada yang lain.
- Simbol “=” menunjukkan bahwa dua bilangan tersebut memiliki nilai yang sama.
Misalnya, jika Anda memiliki dua integer, a dan b, maka Anda dapat menggambarkan perbandingannya sebagai berikut:
- Jika a lebih besar dari b, maka penulisan perbandingan adalah a > b.
- Jika a lebih kecil dari b, maka penulisan perbandingan adalah a < b.
- Sedangkan jika a dan b memiliki nilai yang sama, maka penulisan perbandingan adalah a = b.
Bagaimana Mengurutkan Bilangan Bulat dengan Garis?
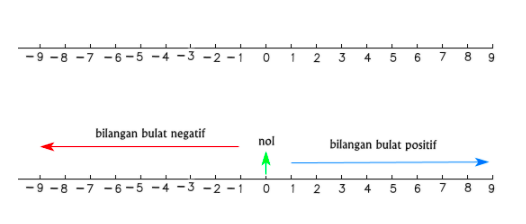
Jika Anda diberi sejumlah bilangan dan diminta untuk mengurutkannya menggunakan garis bilangan, maka langkah pertama adalah membuat garis bilangan itu sendiri.
Garis bilangan adalah representasi visual dari semua bilangan bulat, dengan bilangan negatif di sebelah kiri nol (ditunjukkan dengan panah merah) dan bilangan positif di sebelah kanan nol (ditunjukkan dengan panah biru). Nilai bilangan semakin ke kiri akan semakin kecil dan semakin ke kanan akan semakin besar.
Untuk mengurutkan bilangan, Anda harus merujuk pada garis bilangan. Misalnya, untuk mengurutkan bilangan -4, -8, -3, 6, 5, 7 dari yang terkecil hingga yang terbesar, Anda bisa mulai dengan bilangan paling kiri (-8) dan berakhir dengan yang paling kanan (7), sehingga urutannya adalah -8, -4, -3, 5, 6, 7.
Sedangkan untuk menemukan bilangan yang kurang dari 3 dan lebih dari -5, Anda mencatat bilangan tersebut dari garis bilangan, yaitu -4, -3, -2, -1, 0, 1, 2. Bagaimana, mudah bukan?
Baca Juga : Memahami Sifat-Sifat Eksponen, Fungsi, Rumus, dan Contohnya
Contoh Soal Terkait Bilangan Bulat
Berikut adalah contoh soal untuk mengurutkan bilangan bulat dari yang terkecil hingga yang terbesar:
Urutkan bilangan-bilangan bulat berikut: -3, 8, 13, -15, 1.
Pembahasan:
Pertama, Anda perlu ingat bahwa bilangan positif selalu lebih besar dari bilangan negatif. Jadi, Anda sudah tahu bahwa -3 dan -15 pasti lebih kecil dari 8, 13, dan 1.
Untuk menentukan bilangan yang paling kecil di antara -3 dan -15, Anda bisa menggunakan garis bilangan. Dari garis bilangan, Anda lihat bahwa -15 berada di sebelah kiri -3, yang berarti -15 lebih kecil dari -3, atau dapat ditulis sebagai -15 < -3.

Sekarang, mari susun urutannya:
-15 < -3 < … < … < …
Selanjutnya, Anda lihat bilangan 13 yang mana terletak di sebelah paling kanan garis bilangan. Kondisi ini menunjukkan bahwa 13 adalah bilangan terbesar dalam kumpulan ini.
-15 < -3 < … < … < 13
Terakhir, Anda bandingkan 1 dan 8. Anda tahu bahwa 1 lebih kecil dari 8, sehingga Anda dapat menulis:
-15 < -3 < 1 < 8 < 13
Jadi, urutan bilangan bulat dari yang terkecil ke yang terbesar adalah: -15, -3, 1, 8, 13.
Baca Juga : Apa Itu Bilangan Cacah: Pengertian, Sifat, Jenis, dan Contoh Soal
Sudah Paham dengan Konsep Bilangan Bulat?
Dengan penjelasan dan contoh yang telah diberikan, semoga Anda sekarang telah memahami konsep bilangan bulat atau integer dengan lebih baik. Sebab, integer adalah bagian penting dalam matematika yang mencakup bilangan negatif, nol, dan bilangan positif.
Menggunakan garis bilangan sebagai panduan dapat membantu Anda dalam mengurutkan dan memahami perbandingan antara bilangan-bilangan tersebut. Bilangan ini adalah dasar yang sangat penting untuk memahami matematika lebih lanjut, terutama dalam pemecahan masalah dan analisis data. Selamat belajar!