Masih ingatkah Anda dengan pelajaran matematika saat SD terkait materi bilangan cacah? Saat itu, banyak sekali ragam pembahasan materi hingga Anda mungkin lupa beberapa bagian yang termasuk cacah. Nah, yuk ingat-ingat lagi bagaimana materi bilangan tersebut melalui artikel ini!
Apa Itu Bilangan Cacah?
Secara teori, bilangan bulat atau bilangan cacah adalah jenis bilangan dalam matematika yang digunakan untuk menghitung dan mengidentifikasi jumlah atau urutan objek. Bilangan ini menyatakan cacah anggota atau kardinalitas dalam himpunan.
Jika dalam suatu himpunan tidak memiliki anggota, maka cacah anggota dinyatakan sebagai “nol” dengan lambang “0”. Begitu pula ketika suatu himpunan hanya memiliki satu anggota, maka cacah anggota dinyatakan sebagai “satu” dengan lambang “1”.
Begitu pula untuk bilangan seterusnya, sehingga dalam kamus matematika muncul suatu baris bilangan yang menyatakan hasil pencacahan himpunan, meliputi:
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …..}
Meskipun bagi kalangan awam, atau mungkin Anda, bahwa bilangan cacah termasuk bagian dari bilangan asli, namun faktanya sedikit berbeda. Sebab, bilangan cacah merupakan suatu bilangan asli yang semua angkanya adalah positif dan terdapat angka nol.
Maka dari itu, angka pecahan, desimal, dan negatif bukan bagian dari himpunan pencacahan. Hal ini lantaran salah satu ciri-ciri bilangan ini adalah dimulai dengan angka nol.
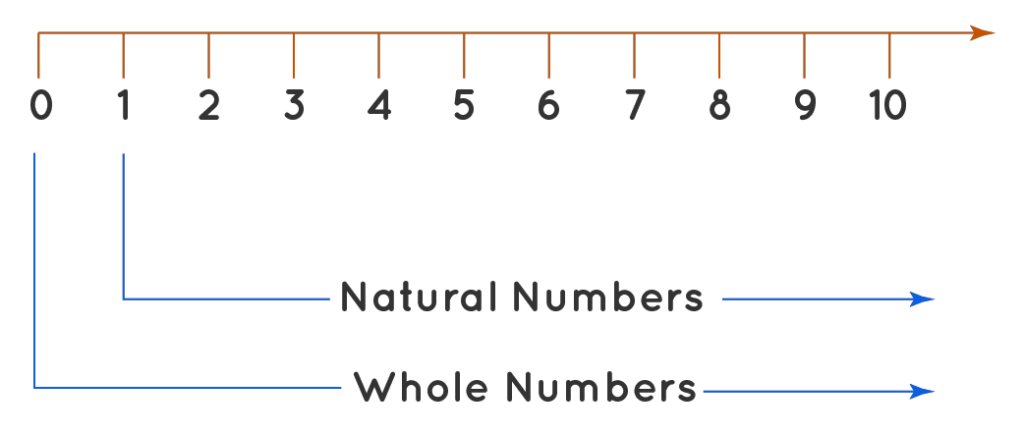
Supaya Anda bisa menuliskannya dengan lebih mudah, notasi matematika yang melambangkan suatu bilangan himpunan pencacah adalah “W”. Lambang tersebut diambil dari istilah bilangan cacah itu sendiri dalam bahasa Inggris, yaitu whole number.
W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …..}
Baca Juga : Bilangan Bulat: Pengertian, Jenis, Urutan, dan Contoh Soal
Sifat-Sifat Bilangan Cacah
Setelah Anda memahami definisinya, Anda bisa meningkatkan pemahaman mengenai bilangan cacah melalui sejumlah sifat. Nah, sifat-sifat ini biasa Anda temui dalam operasi bilangan aritmatika seperti penjumlahan, pengurangan, perkalian, dan pembagian. Berikut ini masing-masing penjelasan dan contoh soalnya:
1. Sifat Tertutup
Sifat yang pertama adalah sifat tertutup untuk perkalian dan penjumlahan. Maksudnya, setiap penjumlahan atau perkalian suatu angka cacah akan menghasilkan bilangan cacah pula. Contohnya penjumlahan 1 + 5 = 6 dan perkalian 3 x 5 = 15.
2. Sifat Komutatif
Sifat selanjutnya adalah ketika posisi bilangan cacahan ditukar, maka hasilnya akan tetap sama. Sebab, pada dasarnya sifat komutatif artinya pertukaran dan meskipun pertukaran terjadi pada operasi penjumlahan atau perkalian, hasilnya tetap sama. Seperti ilustrasi berikut
a + b = b + a
a x b = b x a
Sebagai contoh:
- 1 + 3 = 3 + 1 = 4
- 2 x 3 = 3 x 2 = 6
Akan tetapi, pertukaran ini berlaku untuk satu operasi penjumlahan atau operasi perkalian. Sehingga, sifat ini tidak berlaku apabila dalam satu operasi terdapat penjumlahan dan perkalian sekaligus.
3. Sifat Asosiatif
Sifat bilangan cacah yang ketiga adalah asosiatif yang mana memiliki arti pengelompokan. Apabila terdapat tiga angka penjumlahan atau perkalian, maka hasilnya akan tetap sama meskipun pengelompokannya berbeda.
Biasanya, tanda suatu pengelompokkan bilangan adalah dari adanya tanda kurung. Berikut ilustrasinya:
a + (b + c) = (a + b) + c
a x (b x c) = (a x b) x c
Contoh soal:
- (1 + 2) + 6 = 1 + (2 + 6)
3 + 6 = 1 + 8
9 = 9
- 2 x (5 x 1) = (2 x 5) x 1
2 x 5 = 10 x 1
10 = 10
4. Sifat Distributif
Sifat bilangan cacah selanjutnya adalah distributif. Secara teori, sifat distributif berarti penggabungan, sehingga masing-masing operasi hitung penjumlahan, pengurangan, pembagian, dan perkalian dapat bergabung menjadi satu.
(a + b) x c = (a x c) + (b x c)
Contoh soal:
- (2 + 4) x 3 = (2 x 3) + (4 x 3)
6 x 3 = 6+12
18 = 18
- (9 – 6) x 3 = (9 x 3) – (6 x 3)
3 x 3 = 3 – 2
1 = 1
5. Sifat Perkalian dan Pembagian Nol
Jika suatu angka cacah dikali dengan nol, maka hasilnya adalah nol. Aturan ini berlaku untuk semua angka yang termasuk himpunan cacah.
a x 0 = 0
Berbeda dengan perkalian, jika operasi hitung pembagian terdapat angka cacah yang dibagi dengan nol, maka hasilnya adalah tidak terdefinisi (∞).
Contoh soal:
- 17 x 0 = 0
- 6 : 0 = ∞
Macam-Macam Bilangan Cacah
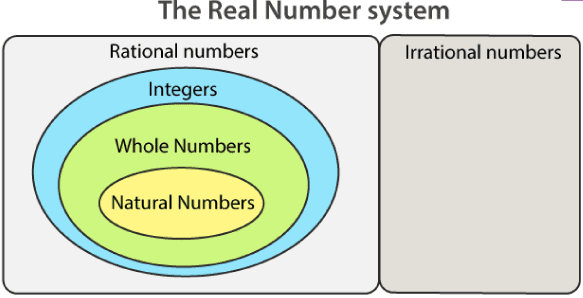
Seperti penjelasan sebelumnya, bilangan cacah merupakan bilangan asli dan ditambah nol. Jika Anda hitung, maka jumlah bilangan asli itu tak terdefinisi yang mana artinya sangat banyak. Maka dari itu, agar pemahamanmu semakin bagus, yuk pelajari macam-macamnya:
1. Bilangan Genap
Bilangan genap merupakan bilangan asli yang habis dibagi dua atau angka yang memiliki kelipatan dua. Nah, untuk mengetahui apa saja bilangan genap yang termasuk himpunan pencacahan, pahami contoh berikut:
W = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …..}
2. Bilangan Ganjil
Berbeda dengan sebelumnya, bilangan ganjil merupakan kebalikan dari bilangan genap. Angka-angka yang termasuk ganjil dalam bilangan cacah adalah sebagai berikut:
W = {3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29. …..}
3. Bilangan Cacah Kuadrat
Bilangan kuadrat merupakan bilangan asli yang dipangkatkan dua. Hasilnya juga akan sama menjadi salah satu bagian dari himpunan pencacahan. Berikut ini bentuk operasi matematikanya:
W = 12, 22, 32, 42, 52, 62, 72, 82, 92, 102……
4. Bilangan Prima
Bilangan prima adalah angka yang hanya dapat dibagi olehnya sendiri dan tidak memiliki faktor-faktor pembagi lainnya. Beberapa contoh bilangan prima yang masuk dalam himpunan pencacahan adalah:
W = {3, 5, 7, 9, 11, 17, 19, ……}
5. Bilangan Cacah Kelipatan Lima
Jika ada soal bilangan dengan kelipatan lima, maka Anda tinggal menuliskan angka pertamanya lima, lalu lanjut dengan kelipatan lima dan seterusnya. Berikut contohnya:
W = {5, 10, 15, 20, 25, 30, ….}
Contoh Soal Bilangan Cacah
Nah, berikut ini terdapat beberapa soal cerita yang bisa Anda selesaikan dengan operasi hitung cacah:
1. Contoh Soal 1
Dari bilangan di bawah ini, tentukan mana saja yang termasuk bilangan cacah!
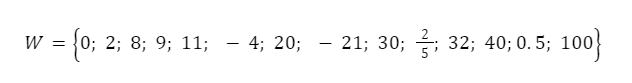
Jawab:
Bilangan yang termasuk dalam himpunan pencacahan adalah semua bilangan positif dan nol. Bilangan desimal, pecahan, dan negatif tidak termasuk himpunan cacah. Jadi jawabannya adalah 0, 1, 8, 9, 11, 20, 30, 32, 40, dan 100.
2. Contoh Soal 2
Pak Rudi membeli satu buah pisang dan rambutan. Harga satu buah pisang adalah Rp15.000,00, sedangkan harga satu kg rambutan adalah Rp10.000, 00. Berapa total belanja Pak Rudi?
Jawab:
Perhitungan bilangan cacah ini bisa menggunakan sifat tertutup:
15.000 + 10.000 = 25.000
3. Contoh Soal 3
Ibu Guru memiliki 15 buah pensil. Pensil itu dibagikan ke beberapa muridnya hingga habis tak bersisa. Masing-masing siswa mendapatkan 3 buah pensil. Maka, berapa total murid yang mendapatkan pensil dari ibu guru?
Cara pertama: 15 / 3=5
Cara kedua: 15 – 3 – 3 – 3 – 3 – 3 = 0
Jawab:
Operasi hitung pembagian dengan konsep ini ada dua cara, yaitu:
Cara pertama menggunakan konsep perhitungan tertutup, sedangkan cara yang kedua adalah memakai konsep pengurangan berulang. Jadi, menghitung hasil akhirnya adalah dengan melihat berapa angka 3 yang muncul pada operasi hitung pengurangan. Jadi jawaban dari soal di atas adalah lima.
4. Contoh Soal 4
Soal ujian fisika terdiri dari 30 soal. Dengan ketentuan penilaian masing-masing soal, jawaban benar akan mendapatkan skor 4, untuk jawaban salah mendapatkan skor -2, dan apabila jawaban kosong memperoleh skor -1.
Jika Tina mengerjakan 25 soal dengan jawaban benar 10 soal, maka berapakah Tina mendapatkan nilai untuk ujian fisika?
Penyelesaian:
Diketahui : jumlah soal : 30 soal
benar : 4 poin
salah : -2 poin
kosong : -1 poin
total soal selesai : 25 soal
jawaban benar : 10 soal
Ditanya : Berapa nilai akhir ujian fisika?
Jawab:
Jawaban salah = total soal selesai – jawaban benar = 25 – 10 = 15 soal
Jawaban kosong = Total soal – Total soal selesai = 30 – 25 = 5 soal
Jadi, skor yang Tina dapatkan adalah:
(10 x 4) + (15 x (-2)) + (5 x (-1)) = 40 + (-30) + (-5) = 5
5. Contoh Soal 5
Kerjakan soal-soal bilangan cacah berikut ini:
- 20 : 4 x 2 = …..
- 2 x 20 : 4 = …..
- 10 + 20 : 5 = …..
- 75 : 15 x5 – 15 = …..
- 40 : 5 x 4 = …..
Jawabannya adalah sebagai berikut:
- 20 : 4 x 2 = 5 x 2 =10
- 2 x 20 : 4 = 40 : 4 = 10
- 10 + (20 : 5) = 10 + 4 =14
- (75 : 15) x 5 – 15 = (5 x 5) – 15 = 10
- (40 : 5) x 4 = 20 x 4 = 80
Tips dan Trik Menghitung Operasi Campuran pada Bilangan Cacah
Sampai di sini, apakah Anda sudah tahu cara menyelesaikan operasi hitung campuran pada bilangan cacah? Nah, dari beberapa soal di atas, terdapat operasi hitung campuran. Supaya lebih mudah mengerjakan, Anda bisa ikuti beberapa tips berikut:
- Jika ada pengurangan, penjumlahan, perkalian, dan pembagian, maka dahulukan pembagian dan perkalian.
- Jika operasi pembagian dan perkalian saja, maka kerjakan yang ada dalam kurung.
- Lalu, jika tidak ada tanda kurung pada operasi kali, bagi, jumlah, dan kurang, maka kerjakan berurutan dari bilangan yang paling kiri.
Walaupun terlihat sangat mudah, namun operasi perhitungan campuran itu butuh ketelitian yang tinggi. Jika Anda tidak menggunakan konsep di atas, maka hasil perhitungan juga akan salah.
Sudah Paham dengan Konsep Bilangan Cacah?
Demikian penjelasan materi matematika tingkat dasar terkait bilangan cacah yang perlu Anda pahami. Pada dasarnya, bilangan cacah adalah konsep matematika yang sangat mendasar dan penting dalam berbagai aplikasi matematika, sains, teknik, dan kehidupan sehari-hari.
Bilangan ini membentuk dasar untuk memecahkan berbagai masalah dan perhitungan. Bahkan dapat membantu Anda untuk mengukur, mengidentifikasi, dan menghitung berbagai hal dalam dunia nyata. Misalnya untuk mengukur berat, jumlah, panjang, waktu, dan banyak aspek lainnya.