Contoh barisan dan deret aritmatika adalah konsep penting dalam matematika yang digunakan untuk menganalisis pola dan melakukan perhitungan. Barisan aritmatika terdiri dari serangkaian bilangan dengan perbedaan tetap antara setiap suku berturut-turut.
Dalam hal ini, contoh barisan dan deret aritmatika membantu dalam memahami rumus dan metode menghitung suku ke-n dalam barisan serta jumlah keseluruhan suku dalam sebuah deret. Untuk informasi selengkapnya seputar deret dan barisan aritmatika, baca artikel ini sampai selesai, ya!
Apa Itu Barisan dan Deret Aritmatika?

Barisan aritmatika adalah urutan di mana setiap bilangan selanjutnya diperoleh dengan menambahkan konstanta yang sama ke bilangan sebelumnya. Konstanta dalam barisan aritmatika disebut sebagai beda atau selisih antara dua suku berturut-turut.
Misalnya, urutan bilangan 2, 5, 8, 11, dan 14 memiliki selisih atau konstanta beda sebesar 3. Berdasarkan contoh tersebut, barisan aritmatika akan berbentuk U1, U1 + b, U1 +2b, U1 +3b, …… hingga n suku.
Secara teori, contoh barisan dan deret aritmatika memiliki hubungan erat. Sebab, deret aritmatika adalah hasil nilai setiap sukunya yang didapatkan melalui penjumlahan dari semua bilangan dalam barisan aritmatika.
Sederhananya, dalam deret aritmatika, Anda perlu menambahkan setiap suku dalam barisan untuk mendapatkan jumlah keseluruhan deret. Misalnya, dalam deret aritmatika 3 + 6 + 9 + 12 + 15, …, jumlah semua suku adalah hasil dari penjumlahan bilangan-bilangan tersebut.
Rumus Barisan dan Deret Aritmatika
Berikut ini adalah beberapa rumus yang perlu Anda gunakan untuk menyelesaikan contoh barisan dan deret aritmatika:
1. Rumus Barisan Aritmatika
Dalam penyelesaian masalah yang melibatkan barisan aritmatika, Anda perlu menggunakan rumus berikut:
Un = a1 + (n – 1) b
Untuk mencari beda (b), gunakan rumus sebagai berikut:
B = Un – Un₋₁
Dalam rumus tersebut, Un adalah suku ke-n dalam barisan aritmatika dan Un₋₁ adalah suku sebelum suku n. Kemudian, a1 adalah suku pertama dalam barisan aritmatika, n adalah jumlah suku yang ingin Anda temukan, dan b adalah beda atau selisih antara dua suku berturut-turut.
2. Rumus Deret Aritmatika
Dalam penyelesaian masalah yang melibatkan deret aritmatika, Anda perlu menggunakan rumus berikut:
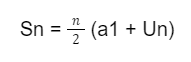
Dalam rumus tersebut, Sn adalah jumlah dari n suku pertama dalam deret aritmatika dan a1 adalah suku pertama dalam deret aritmatika. Lalu, Un adalah suku ke-n dalam deret aritmatika dan n adalah jumlah suku yang ingin Anda tambahkan.
Baca Juga : 10 Contoh Soal Induksi Matematika dengan Pembuktian dan Materi
Contoh Barisan dan Deret Aritmatika serta Penyelesaiannya

Untuk pemahaman lebih dalam, mari kita pelajari beberapa contoh barisan dan deret aritmatika beserta penyelesaiannya berikut ini:
1. Contoh Soal Barisan Aritmatika
Adapun contoh dan penyelesaian soal barisan aritmatika adalah sebagai berikut:
1. Contoh Soal 1
Temukan persamaan untuk suku umum dari deret aritmatika yang diberikan dan gunakan untuk menghitung suku ke-100: 7,10,13,16,19,…
Penyelesaian:
Dalam penyelesaian barisan aritmatika, Anda bisa menggunakan rumus umum yang diberikan sebelumnya, yaitu Un = a1 + (n – 1) b. Untuk menemukan rumus beda (b), Anda dapat menggunakan rumus: b = Un – Un₋₁.
Mari kita gunakan contoh barisan aritmatika yang diberikan: 7, 10, 13, 16, 19, …
Langkah pertama adalah menemukan beda (b) antara dua suku berturut-turut. Anda akan menggunakan rumus b = Un – Un₋₁.
Misalkan Anda ingin mencari beda antara suku kedua dan suku pertama, maka Anda dapat menggantikan nilai Un = 10 dan Un₋₁ = 7 ke dalam rumus tersebut:
b = 10 – 7 = 3
Dalam contoh barisan dan deret aritmatika ini, nilai beda (b) adalah 3. Dengan mengetahui nilai beda ini, Anda dapat menggunakan rumus umum Un = a1 + (n – 1) b untuk mencari suku-suku lain dalam deret.
Misalkan, Anda ingin mencari suku ke-100 dalam deret ini. Anda bisa menggunakan rumus Un = a1 + (n – 1) b dan menggantikan nilai-nilai yang diketahui:
Un = a1 + (100 – 1) b
Un = 7 + (99) (3) = 7 + 297 = 304
Jadi, suku ke-100 dalam deret ini adalah 304.
Dengan demikian, penggunaan rumus Un = a1 + (n – 1) b dan mengetahui nilai beda (b) dapat membantu Anda dalam mencari suku-suku dalam deret aritmatika yang diberikan dengan lebih mudah.
2. Contoh Soal 2
Temukan semua istilah di antaranya U1 = −8 dan U7 = 10 dari barisan aritmatika. Dengan kata lain, temukan semua rata-rata aritmatika antara suku 1 dan 7!
Penyelesaian:
Langkah pertama adalah mencari beda (b) antara dua suku berturut-turut. Anda akan menggunakan rumus b = Un – Un₋₁.
Misalkan, Anda ingin mencari beda antara suku ketujuh (a7) dan suku keenam (a6). Anda dapat menggantikan nilai Un = 10 dan Un₋₁ = 7 ke dalam rumus tersebut:
b = 10 – 7 = 3
Dalam contoh barisan dan deret aritmatika yang ada, nilai beda (b) adalah 3. Dengan mengetahui nilai beda ini, Anda dapat menggunakan rumus umum Un = a1 + (n – 1) b untuk mencari suku-suku lain dalam deret.
Selanjutnya, Anda akan menggunakan suku pertama (a1 = -8) dan beda (b = 3) untuk mencari persamaan untuk suku ke-n dalam deret. Anda akan menggunakan rumus Un = a1 + (n – 1) b dan menggantikan nilai-nilai yang diketahui:
Un = -8 + (n – 1) 3
Un = -8 + 3n – 3 = -11 + 3n
Jadi, persamaan untuk suku ke-n dalam deret ini adalah Un = -11 + 3n, di mana n adalah bilangan bulat positif.
Sekarang, Anda dapat menggunakan persamaan tersebut untuk mencari suku-suku yang hilang antara suku pertama (a1) dan suku ketujuh (a7). Mari kita substitusikan nilai n = 2, 3, 4, 5, dan 6 ke dalam persamaan Un = -11 + 3n:
- a2 = -11 + 3(2) = -11 + 6 = -5
- a3 = -11 + 3(3) = -11 + 9 = -2
- a4 = -11 + 3(4) = -11 + 12 = 1
- a5 = -11 + 3(5) = -11 + 15 = 4
- a6 = -11 + 3(6) = -11 + 18 = 7
Jadi, suku-suku yang hilang antara suku pertama (a1 = -8) dan suku ketujuh (a7 = 10) adalah -5, -2, 1, 4, dan 7.
2. Contoh Soal Deret Aritmatika
Adapun contoh dan penyelesaian soal deret aritmatika adalah sebagai berikut:
Dalam amfiteater luar ruangan, jumlah kursi di setiap baris bertambah 2 dari baris sebelumnya. Baris pertama memiliki 26 kursi, baris kedua memiliki 28 kursi, dan seterusnya. Hitung total kapasitas tempat duduk teater jika ada 18 baris!
Penyelesaian:
Untuk mencari total kapasitas tempat duduk, Anda perlu menjumlahkan jumlah kursi di setiap baris. Berhubung jumlah kursi di setiap baris membentuk urutan dengan penambahan 2, Anda dapat menggunakan rumus contoh barisan dan deret aritmatika untuk jumlah urutan aritmatika.
Jumlah kursi di baris pertama (a1) adalah 26. Kemudian, beda antara dua baris berturut-turut (b) adalah 2. Sedangkan jumlah baris (n) adalah 18.
Dengan menggunakan rumus jumlah deret aritmatika Sn = n2 (a1 + Un), Anda dapat mencari total kapasitas tempat duduk teater. Substitusikan nilai-nilai yang diketahui ke dalam rumus:
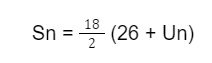
Anda perlu mencari nilai Un, yaitu jumlah kursi di baris ke-18. Anda dapat menggunakan rumus umum Un = a1 + (n – 1) b, di mana Un adalah jumlah kursi di baris ke-n.
Sehingga, substitusikan nilai a1 = 26, n = 18, dan b = 2 ke dalam rumus:
Un = 26 + (18 – 1) 2
Un = 26 + (17 x 2) = 26 + 34 = 60
Kemudian, substitusikan nilai Un = 60 ke dalam rumus Sn:
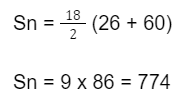
Jadi, total kapasitas tempat duduk teater adalah 774.
Sudah Paham dari Contoh Barisan dan Deret Aritmatika?
Dari contoh barisan dan deret aritmatika yang telah kita bahas, Anda dapat melihat bagaimana rumus-rumus tersebut sangat berguna untuk menyelesaikan masalah yang melibatkan pola penambahan atau pengurangan yang teratur.
Dengan memahami konsep dasar seperti suku pertama, beda, dan rumus umum, Anda dapat mudah mencari suku-suku dalam deret dan menghitung jumlah totalnya. Pengetahuan tentang barisan dan deret aritmatika dapat menerapkan dalam berbagai konteks, seperti matematika, ilmu pengetahuan, ekonomi, dan sebagainya.
Pemahaman akan konsep ini membuat Anda dapat mengembangkan keahlian dalam menganalisis pola dan merumuskan solusi untuk berbagai masalah yang melibatkan urutan angka atau objek. Semangat belajar!

