Tahukah Anda? Kesebangunan telah menjadi salah satu konsep penting dalam matematika yang berguna untuk membandingkan dan mengukur proporsi antara dua atau lebih bentuk atau bangun datar yang serupa. Untuk pemahaman lebih lanjut, mari kita lihat beberapa contoh soal kesebangunan dan penjelasannya di artikel ini!
Apa Itu Kesebangunan?
Sebagai pengantar materi, kesebangunan adalah istilah yang menggambarkan dua buah bangun datar yang sama dan memiliki sudut yang sama besar, tetapi ukurannya berbeda. Bentuk bangun datar ini seperti memperbesar atau memperkecil ukuran.
Seperti yang sudah Anda pahami, banyak contoh soal kesebangunan yang telah menyatakan syarat dua bangun datar yang sebangun. Anda akan diperkenalkan lagi terkait dua ciri yang paling menonjol untuk mengatakan bahwa dua buah bangun datar tersebut adalah sebangun. Berikut ini penjelasannya:
- Perbandingan panjang sisi-sisinya sama besar, yaitu berupa:
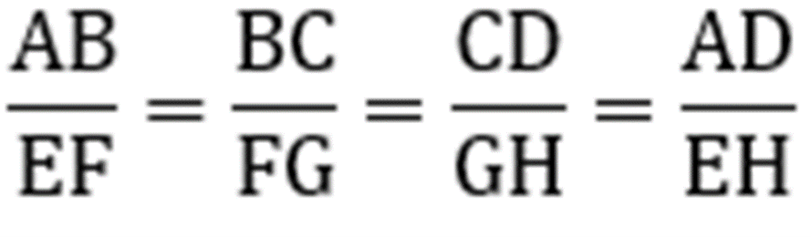
- Kedua sudut yang bersesuaian memiliki besar yang sama:
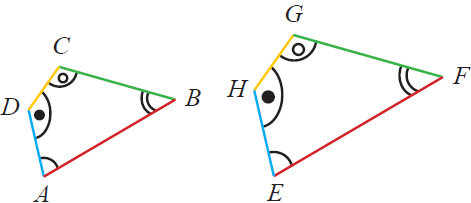
Ciri-ciri bangun datar yang sebangun juga berlaku untuk dua buah segitiga sama sisi maupun segitiga siku-siku. Sebab, jika ada dua buah segitiga yang panjang sisinya sama dan masing-masing sudutnya bersesuaian sama besar meskipun terletak di posisi yang berbeda, maka segitiga tersebut bersifat sebangun.
Lalu, jika Anda sudah menemukan segitiga atau bangun datar lain yang sebangun, maka Anda bisa menuliskannya dengan simbol notasi “~”.
Banyak buku atau sumber yang menyatakan objek kesebangunan dengan garis maupun bangun datar seperti jajar genjang, trapesium, persegi, dan persegi panjang. Selain itu, kesebangunan juga dapat diterapkan dalam konteks aljabar, misalnya untuk menyatakan kesamaan polinomial maupun sistem persamaan.
Walaupun kesebangunan selalu berhubungan dengan bentuk dan struktur dua benda yang berbeda. Sebenarnya, kesebangunan itu juga menyiratkan kesamaan dan perbedaan lain yang konteksnya lebih luas daripada matematika.
10 Contoh Soal Kesebangunan dan Pembahasannya

Nah, penjelasan di atas cukup membuat Anda mengingat apa itu kesebangunan, bukan? Dalam soal-soal kesebangunan, sering kali muncul tentang perbandingan dan pembuktian apakah bangun tersebut termasuk kategori sebangun atau tidak. Berikut ini beberapa contoh soal kesebangunan yang bisa Anda pelajari:
1. Contoh Soal 1
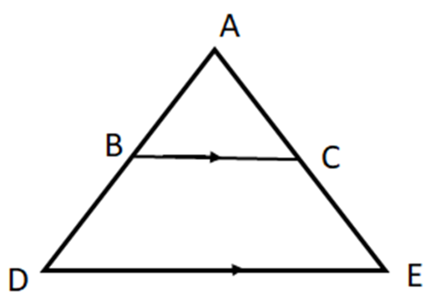
Pada gambar di atas, terdapat dua buah segitiga ABC dan ADE. Tunjukkan apakah dua bangun segitiga tersebut sebangun atau tidak!
Pembahasan:
Anda bisa lihat bahwasannya sudut ABC bersesuaian dengan sudut ADE. Sebab, garis BC // DE dan sudut ABC sehadap dengan sudut ADE.
Begitu juga dengan sudut BAC = DAE, karena sudut BAC dan DAE saling berhimpit. Oleh karena itu, dua buah segitiga ABC dan ADE adalah sebangun.
Hal itu disebabkan keduanya memenuhi syarat kesebangunan pada segitiga, yaitu memiliki dua sudut yang bersesuaian dengan besar yang sama.
2. Contoh Soal 2
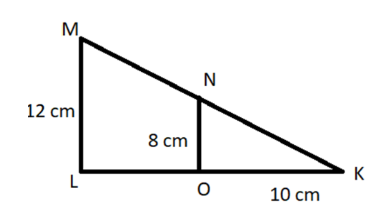
Perhatikan gambar di atas. Sesuai dengan keterangan panjang garis masing-masing, maka tentukanlah panjang garis OL!
Pembahasan:
Pada contoh soal kesebangunan tersebut, terdapat segitiga KLM yang lebih besar daripada segitiga KNO. Dengan bentuk yang sama, maka segitiga tersebut adalah sebangun.
Lalu, untuk menemukan nilai panjang garis OL, langkah pertama yang harus Anda lakukan adalah menemukan panjang sisi KL. Kemudian, Anda bisa buat perbandingan alas dan tinggi pada kedua segitiga tersebut. Berikut ilustrasi rumus dan caranya:
OL = KL – KO
OL = 15 cm – 10 cm = 5 cm
3. Contoh Soal 3
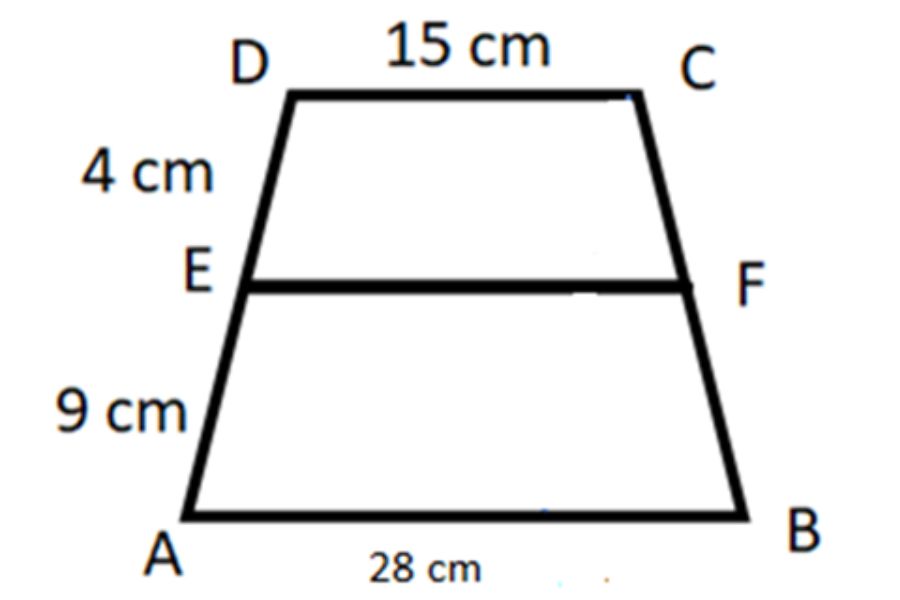
Dari soal bangun datar trapesium di atas, tentukan panjang EF!
Pembahasan:
Sebelum mengerjakan contoh soal kesebangunan ini, sebaiknya Anda membuat garis bantuan serta melengkapi panjang masing-masing garis yang diketahui.
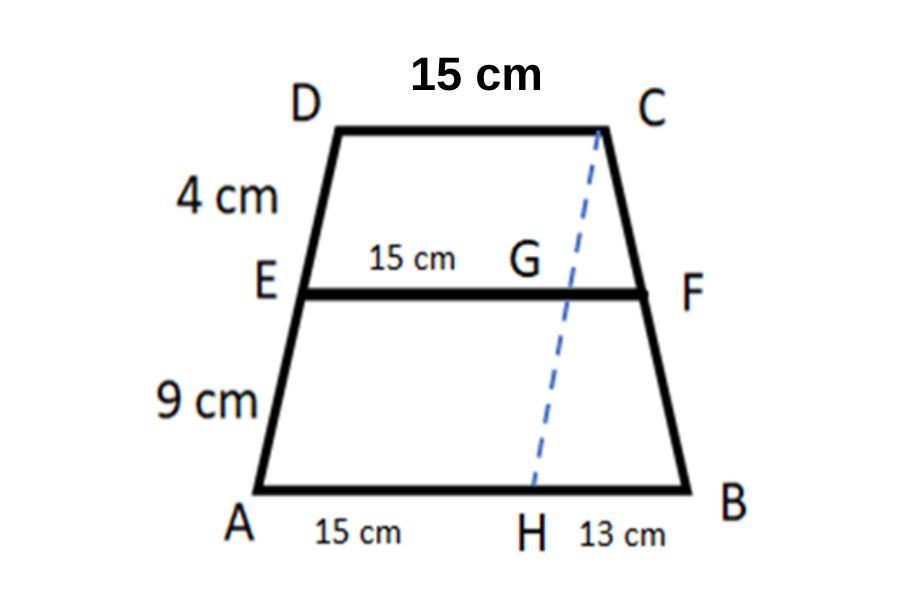
Nah, sekarang Anda bisa lebih mudah untuk menyelesaikan soalnya, karena ada data baru yang bisa Anda jadikan bantuan perhitungan. Seperti pada soal sebelumnya, sebaiknya buatlah perbandingan dua segitiga sebangun, yaitu GFC dan HBC.
Dengan demikian, Anda bisa mendapatkan panjang EF dengan cara menjumlahkan garis EG dan GF, sehingga hasilnya adalah
EF = EG + GF
EF = 15 + 4 = 19 cm
4. Contoh Soal 4
Pada hari senin pagi, seorang siswa yang memiliki tinggi badan 150 cm sedang berdiri menghadap tiang bendera. Terlihat adanya bayangan siswa sepanjang 2,5 m dan panjang bayangan tiang bendera sebesar 6 m. Berapakah tinggi sebenarnya dari tiang bendera tersebut?
Pembahasan:
Diketahui:
- Tinggi siswa = 150 cm
- Panjang bayangan siswa = 2,5 m = 250 cm
- Panjang bayangan tiang = 6 m = 600 cm
Anda bisa menyelesaikan soal di atas dengan ilustrasi gambar seperti berikut:
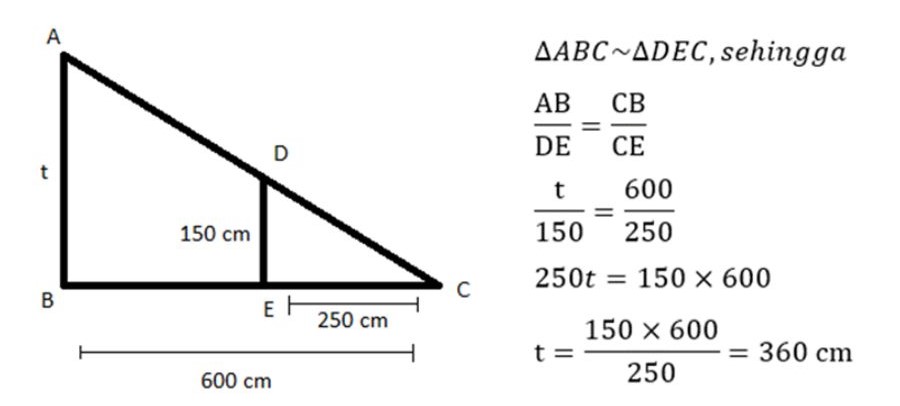
Jadi, tinggi tiang bendera tersebut adalah 360 cm atau 3,6 m.
5. Contoh Soal 5
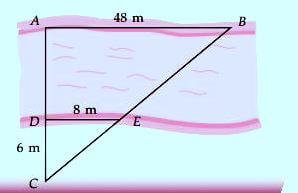
Seorang penyelam berniat untuk mengukur lebar sungai. Panjang tepi sungai (AB) yang berhasil penyelam ukur adalah 48 m. Posisi penyelam saat ini berada di titik C, dengan panjang DC adalah 6 m sedangkan DE adalah 8 m. Berapakah lebar sungai tersebut?
Pembahasan:
Pada contoh soal kesebangunan di atas, Anda harus mencari lebar sungai, di mana lebar sungai pada gambar adalah AD. Maka rumus dan caranya adalah sebagai berikut:
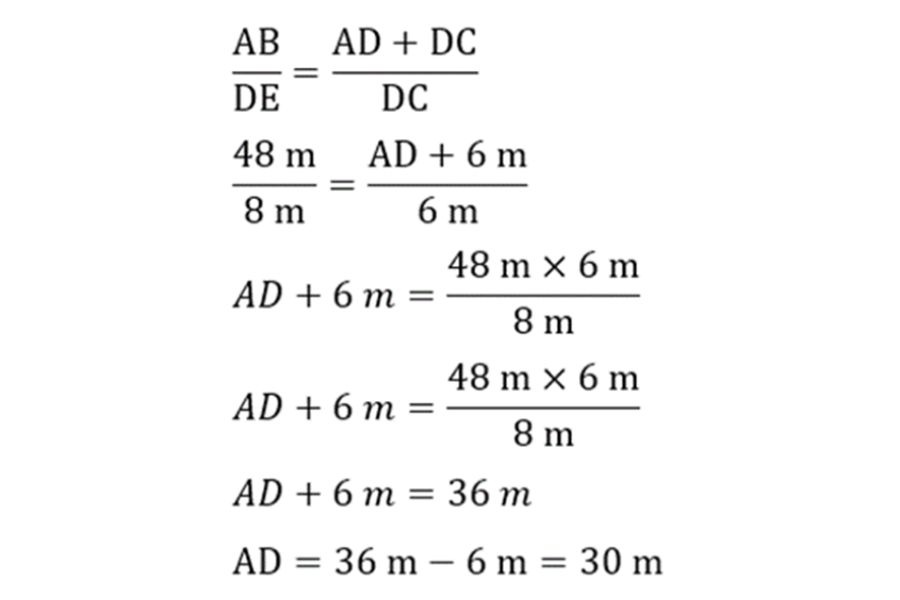
Jadi, lebar sungai yang berhasil penyelam ukur adalah 30 m.
6. Contoh Soal 6
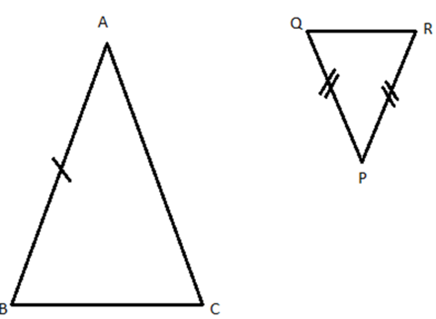
Perhatikan gambar segitiga ABC dan PQR di atas. Jika kedua segitiga tersebut adalah sebangun, serta sudut BAC diketahui sebesar 45o, maka berapakah sudut PQR?
Pembahasan:
Berdasarkan sifat kesebangunan, maka gambar yang ada pada contoh soal kesebangunan tersebut memiliki sudut yang sama pada sudut QPR = BAC = 45o. Segitiga PQR merupakan segitiga sama kaki, maka sudut PQR = sudut PRQ, sehingga:
Sudut PQR + PRQ + QPR = 180o
Sudut PQR + PQR + 45o = 180o
2 sudut PQR = 180o – 45o = 135o
Sudut PQR = 67.5o
7. Contoh Soal 7
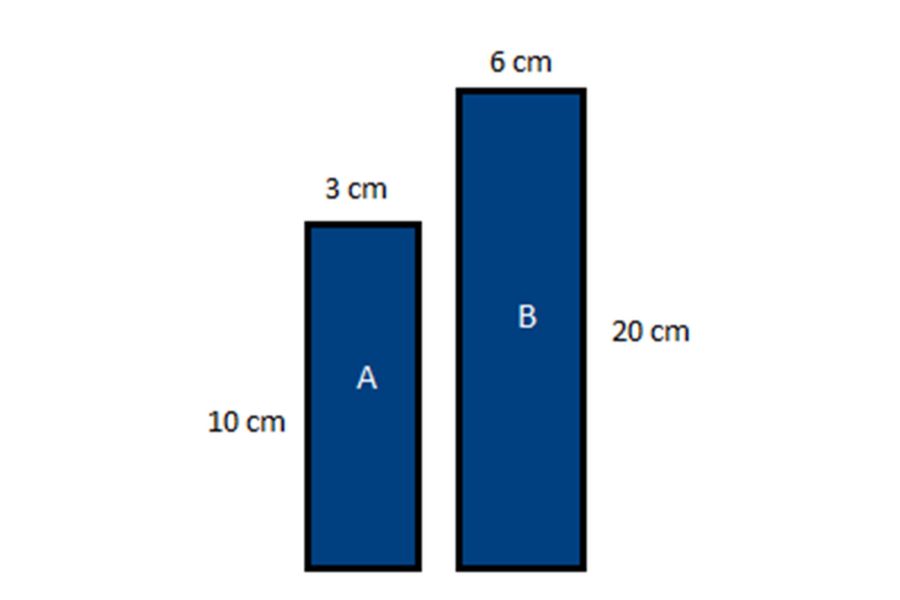
Jika dua buah persegi panjang tersebut sebangun. Maka, berapa perbandingan panjang masing-masing sisi yang sesuai?
Pembahasan:
Anda perlu membandingkan sisi yang bersesuaian, yaitu:
10 / 20 = 3 / 6
1 / 2 = 1 / 2
8. Contoh Soal 8
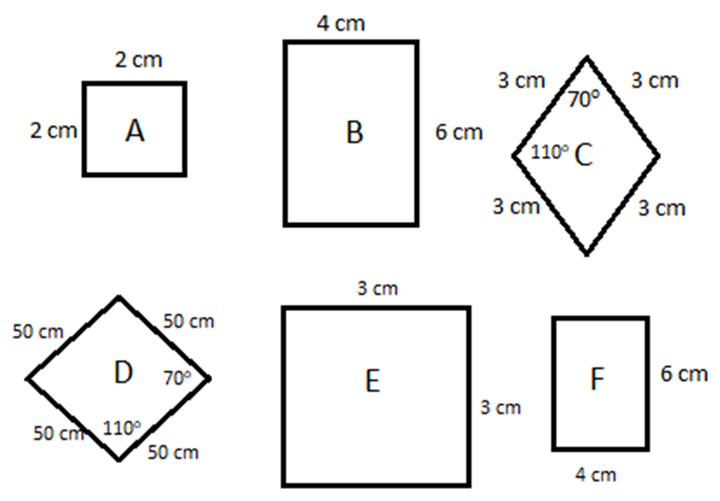
Terdapat beberapa bangun datar di atas, manakah pasangan bangun datar yang sebangun?
Pembahasan:
Pasangan bangun datar sebangun adalah bangun datar yang memiliki panjang sisi bersesuaian dan besarnya masing-masing sudut sama. Sehingga, jawabannya adalah A dan E serta D dan C. Sebab, perbandingan panjang sisi yang diperoleh bangun datar A dan E adalah 2/3 sedangkan bangun datar D dan C adalah 5/3.
9. Contoh Soal 9
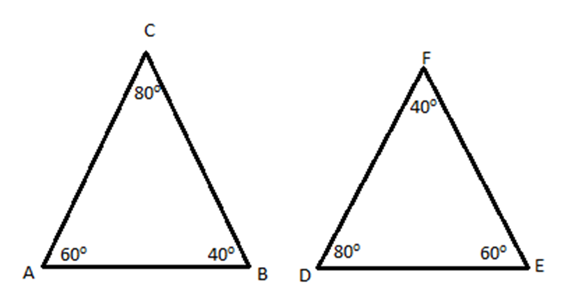
Sudut manakah yang memiliki pasangan sisi bersesuaian?
Pembahasan:
Pasangan sudut yang bersesuaian adalah AB/EF = AC/DE = BC/FD
10. Contoh Soal 10
Perhatikan beberapa pernyataan di bawah ini:
- Dua buah bangun datar segi lima yang beraturan.
- Dua bangun layang-layang.
- Dua buah segitiga sama sisi.
- Dua buah segitiga sama kaki.
- Dua buah jajar genjang berbentuk persegi.
Manakah pasangan di atas yang sebangun?
Pembahasan:
Pasangan yang sebangun adalah I, III, V karena ketiganya memiliki kesamaan perbandingan sisi dan besar sudut.
Baca Juga : Pengertian Kesebangunan dan Kekongruenan Beserta Sifatnya
Asah Kemampuan dengan Berlatih Contoh Soal Kesebangunan!
Bagaimana, sudah cukup paham dengan kesepuluh contoh soal kesebangunan di atas? Soal-soal tersebut bisa Anda pahami untuk melatih kemampuan geometri dalam menganalisa soal kesebangunan.
Semakin sering Anda berlatih, maka kemampuan Anda dalam berhitung dan memberikan keputusan solusi penyelesaian soal jadi lebih mudah. Terlepas dari itu, Anda akan menjadi seorang yang mampu berpikir kritis, menyelesaikan masalah, serta lebih mudah memahami segala ilmu di lain bidang.

