14 Contoh Soal Suku Banyak dan Pembahasannya

Kamu tentu sudah mengenal tentang persamaan kuadrat ketika belajar matematika, kan? Persamaan kuadrat adalah sistem persamaan, di mana pangkatnya ada dua. Cara menentukannya adalah menggunakan pemfaktoran dan kuadrat sempurna. Namun, bagaimana jika pangkatnya lebih dari dua. Adakah contoh soal suku banyak?

Atau sebelum itu, bagaimana cara menentukan suku-suku dalam persamaan, di mana memiliki pangkat lebih dari dua? Nah, sistem persamaan dengan pangkat lebih dari dua ini disebut juga sebagai polinomial atau suku banyak. Ingin tahu lebih lanjut? Simak terus ulasan ini sampai selesai!

Apa Itu Suku Banyak?

Suku banyak merupakan salah satu bentuk operasi aljabar dalam Ilmu Matematika. Umumnya, operasi suku banyak terdiri dari operasi penjumlahan, pengurangan, perkalian, dan pembagian. 

Contoh persamaan dari sistem ini adalah x³ + 2x² + 3x – 4 = 0. Ada pula teorema sisa untuk mengetahui sisa hasil bagi suku banyak secara langsung.

Secara sederhana, rumus umum persamaan suku banyak adalah:

P(x) = a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + …. + a₁x + a₀

Keterangan:

• Derajat (n) merupakan pangkat tertinggi dari suatu suku banyak.
• Variabel (x) merupakan bilangan dengan lambang huruf, misalnya x.
• Koefisien (a) merupakan bilangan yang mengikuti variabel.

Pada contoh soal suku banyak operasi penjumlahan, pengurangan, dan perkalian suku banyak, ada operasi dasar yang sama. Ini berlaku apabila f(x) dan g(x) adalah suku banyak dengan derajat m dan n. Maka teorema yang bisa menjadi patokan adalah:

• f(x) ± g(x) adalah suku banyak dengan derajat maksimum m atau n. 
• f(x) x g(x) adalah suku banyak dengan derajat (m + n). 

Teorema Sisa Suku Banyak

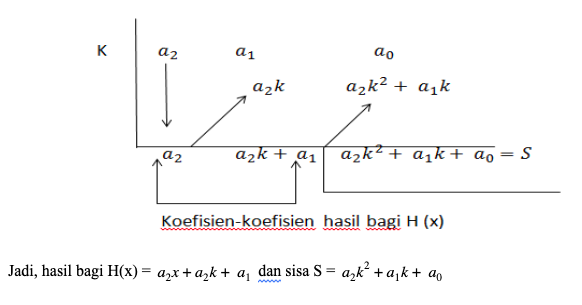
Sementara itu, jika suku banyak f(x) = a₂x² + a₁x + a₀ dibagi dengan P(x) menunjukkan hasil bagi H(x) dan sisa S. Maka, konsep teorema sisa yang berlaku adalah:

 f(x) = P(x) . H(x) + S(x)

Keterangan:

Apabila f(x) memiliki derajat n, P(x) memiliki derajat m (m ≤ n), maka derajat H(x) adalah (n – m) dan derajat maksimum S(x) adalah (m – 1).

Ada dua syarat pembagi untuk teorema sisa, yaitu pembagi dengan (x – k) dan pembagian dengan (ax + b). Berikut ini aturannya:

1. Pembagian dengan (x – k)

Apabila contoh soal suku banyak f(x) dengan derajat n dibagi (x – k), maka sisa S = f(k). Nilai suku banyak x = k dapat ditentukan dengan menerapkan strategi substitusi maupun strategi skema.

2. Pembagian dengan (ax + b)

Apabila suku banyak dengan derajat n dibagi (ax + b), maka sisa S adalah f(-a/b). Sisa ini adalah nilai suku banyak x = -a/b dan dapat ditentukan dengan strategi substitusi maupun skema.

Pembagian Suku Banyak Metode Horner

Ada pula aturan penggunaan metode horner untuk operasi pembagian suku banyak adalah:

1. Tempatkan seluruh koefisien dari derajat tertinggi sampai nol di bagian atas. Semua selalu berawal dari pangkat tertinggi dan berurutan. Apabila terdapat suku banyak dengan salah satu pangkatnya tidak ada, maka koefisien pangkat x³ bisa diganti 0. Misalnya, 2x⁴ + 3x² – 5x – 9 = 0.

2. Tempatkan faktor pengali di bagian sisi kiri.

3. Hasil bagi adalah bagian baris bawah di samping kiri, sementara sisa berada di samping kanan. Maka, rumusnya adalah:

Hasil bagi = kolom bagian kiri / koefisien derajat pembagi

Sisa = kolom bagian kanan

Contoh Soal Suku Banyak dan Pembahasan

Berikut berbagai macam contoh soal yang bisa kamu pelajari untuk memperdalam pemahaman kamu:

Contoh Soal Suku Banyak 1

Jika f(x) = 2x³ + 4x² + 6x + 8 dan g(x) = 7x² – 9x – 11, maka hasil dari f(x) + g(x) adalah …

Pembahasan:

f(x) +g(x) = (2x³ + 4x² + 6x + 8) + (7x² – 9x – 11)

= 2x³ + (4 + 7)x² + (6 – 9)x + 8 -11

= 2x³ + 11x² – 3x – 3

Jadi, hasil penjumlahan f(x) + g(x) adalah 2x³ + 11x² – 3x – 3.

Contoh Soal Suku Banyak 2

Diketahui f(x) = 2x³ + 5x² + 9x + 10 dan g(x) = 4x³ + 7x² – 10x + 5. Tentukan nilai dari f(x) + g(x)!

Pembahasan:

f(x) + g(x) = (2x³ + 5x² + 9x + 10) + (4x³ + 7x² – 10x + 5)

f(x) + g(x) = (2+4)x³ + (5+7)x² + (9+10)x + (10+5)

= 6x³ + 12x² + 19x + 15

Jadi, nilai dari f(x) + g(x) adalah 6x³ + 12x² + 19x + 15

Contoh Soal Suku Banyak 3

Jika P(x) = 3x – 3x² – 1 dan Q(x) = 3x² + x – 2. Maka operasi penjumlahan dari P(x) + Q(x) dan derajatnya adalah…

Pembahasan:

P(x) + Q(x) = (3x – 3x² – 1) + (3x² + x – 2)

P(x) + Q(x) = – 3x² + 3x² + 3x + x -1 – 2

= 4x – 3

Jadi, hasil penjumlahan dari P(x) + Q(x) adalah 4x – 3. Persamaan suku banyak ini memiliki nilai pangkat tertinggi 1, sehingga termasuk suku banyak dengan derajat 1.

Contoh Soal Suku Banyak 4

Diketahui f(x) = 5x⁴ + 7x² – 3x + 5 dan g(x) = 4x⁴ – 8x³ + 2x + 10. Tentukan nilai dari f(x) -g(x)!

Pembahasan:

f(x) – g(x) = (5x⁴ + 7x² – 3x + 5) – (4x⁴ – 8x³ + 2x + 10)

f(x) – g(x) = (5 – 4)x⁴ – (- 8x³) + 7x² + (- 3 – 2)x + 5 – 10

= x⁴ + 8x³ + 7x² – 5x – 5

Jadi, hasil pengurangan dari f(x) – g(x) adalah x⁴ + 8x³ + 7x² – 5x – 5

Contoh Soal Suku Banyak 5

Berikut ini diketahui f(x) = 5x³ + 5x² + 17x + 10 dan g(x) = x³ + 2x² + 10x + 5. Berapakah nilai dari f(x) – g(x)?

Pembahasan:

f(x) – g(x) = (5x³ + 5x² + 17x + 10) – (x³ + 2x² + 10x + 5)

f(x) – g(x) = (5-1)x³ + (5-2)x² + (17-10)x + (10-5)

= 4x³ + 3x² + 7x + 5

Jadi, hasil pengurangan dari f(x) – g(x) adalah 4x³ + 3x² + 7x + 5.

Contoh Soal Suku Banyak 6

Jika P(x) = 2x⁴ – 5x³ + 6x² – x – 2 dan Q(x) = x⁵ – 1. Tentukan hasil dari P(x) – Q(x) beserta derajatnya!

Pembahasan:

P(x) – Q(x) = (2x⁴ – 5x³ + 6x² – x – 2) – (x⁵ – 1)

P(x) – Q(x) = 2x⁴ – 5x³ + 6x² – x – x⁵ + 1

= – x⁵ + 2x⁴ – 5x³ + 6x² – x + 1

Jadi, hasil pengurangan dari P(x) – Q(x) adalah – x⁵ + 2x⁴ – 5x³ + 6x² – x + 1. Di mana nilai pangkat tertingginya adalah 5, sehingga termasuk suku banyak dengan derajat 5.

Contoh Soal Suku Banyak 7

Tentukan hasil perkalian dari dua suku banyak berikut (2x² + 6)(x³ – x + 2)!

Pembahasan:

Untuk menyelesaikan soal ini, kamu bisa menggunakan sifat distributif, berikut caranya:

(2x²)(x³) + (2x²)(-x) + (2x²)(2)+(6)(x³) + (6)(-x)+(6)(2)

f(x) = 2x²⁺³ – 2x²⁺¹ + 4x²⁺⁰ + 6x³ – 6x+12

f(x) = 2x⁵ – 2x³ + 4x² + 6x³ – 6x+12

= 2x⁵ + (-2+6)x³ + 4x² – 6x+12

= 2x⁵ + 4x³ + 4x² – 6x+12

Jadi, hasil perkalian dari dua suku banyak tersebut adalah 2x⁵ + 4x³ + 4x² – 6x+12

Contoh Soal Suku Banyak 8

Carilah sisa pembagi suku banyak 8x³-2x²+5 dengan (x+2)!

Pembahasan:

Kamu bisa menyelesaikan soal ini dengan menggunakan strategi substitusi seperti berikut:

f(x) = 8x³ – 2x² + 5 

f(-2) = 8(-2)³ – 2(-2)² + 5

= -64 – 8 + 5 = -67

Jasi, sisa S dalam persamaan suku banyak di atas adalah -67.

Cara kedua yang bisa kamu lakukan adalah menggunakan strategi skema atau bagan dengan pembagian (x-k). Berikut skemanya:

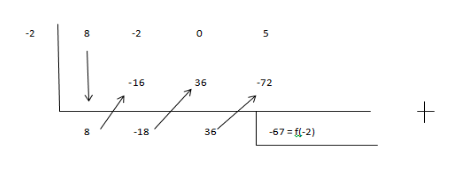
Contoh Soal Suku Banyak 9

Tentukan sisa hasil bagi dari f(x) = x³ – 9x + 14 oleh x-3!

Pembahasan:

Sesuai konsep sisa, f(x) yang dibagi dengan (x-k) sisanya atau S = f(k). Maka (x-k) = (x-3) sehingga nilai k = 3, kemudian substitusikan k = 3 ke dalam persamaan f(x) = x³ – 9x + 14.

f(3) = 3³ – 9(3) + 14

= 27 – 27 + 14 = 14

Jadi, sisa hasil bagi persamaan di atas adalah 14.

Contoh Soal Suku Banyak 10

Tentukan sisa pembagian dari persamaan suku banyak 3x³ + 6x² – 5x – 6 oleh x² + 2x + 3!

Pembahasan:

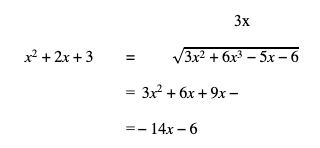
Jadi, sisa pembagian dari persamaan di atas adalah -14x – 6.

Contoh Soal Suku Banyak 11

Terdapat dua suku banyak x³ – 4x² + 5x + m dan x² + 3x -2, jika dibagi dengan x + 1 akan mempunyai sisa sama, maka berapakah nilai dari 2m + 5?

Pembahasan:

Diketahui f(x) = x³ – 4x² + 5x + m

g(x) = x² + 3x – 2

Apabila dibagi (x + 1) => x = -1 mempunyai sisa yang sama. Maka:

f(-x) = g(-1)

x³ – 4x² + 5x + m = x² + 3x – 2

(-1)³ – 4(-1)² + 5(-1) + m = (-1)² + 3(-1) – 2

-1 – 4 – 5 + m = 1 – 3 – 2

– 10 + m = – 4

m = -4 + 10 = 6

Selanjutnya, masukkan nilai m ke dalam 2m + 5, sehingga menjadi 2(6) + 5 = 17. Jadi, nilai dari 2m + 5 adalah 17.

Contoh Soal Suku Banyak 12

Diketahui persamaan suku banyak f(x) = x³ + ax² – bx – 5 dibagi dengan (x – 2), menunjukkan hasil bagi dan sisa 17. Berapakah nilai dari a + b?

Pembahasan:

Dalam contoh soal tipe ini, kamu bisa menggunakan rumus teorema sisa, seperti berikut:

f(x) = H(x). P(x) + sisa

f(x) = (x-2)(x² + 4x + 11) + 17

= x³ + 4x² + 11x – 2x² – 8x – 22 + 17

= x³ + 2x² + 3x – 5

Berdasarkan persamaan suku banyak f(x) = x³ + ax² – bx – 5 dan hasil perhitungan yang diperoleh, dapat diketahui bahwa nilai a adalah 2 dan nilai b adalah -3. Maka, nilai dari a + b = 2 + (-3) = -1. 

Contoh Soal Suku Banyak 13

Diketahui, suatu persamaan suku banyak f(x) = x³ – 4x² + px + 6 dan g(x) = x² + 3x – 2 dibagi dengan (x + 1) memiliki sisa yang sama. Maka, berapakah nilai p dalam persamaan tersebut?

Pembahasan:

(x + 1) => x = -1

Maka, f(-1) = g(-1)

x³ – 4x² + px + 6 = x² + 3x – 2 

(-1)³ – 4(-1)² + p(-1) + 6 = (-1)² + 3(-1) – 2 

-1 – 4 – p + 6 = 1 – 3 – 2

– p = -4 -1

p = 5

Jadi, nilai p dalam persamaan suku banyak f(x) = x³ – 4x² + px + 6 adalah 5

Contoh Soal Suku Banyak 14

Diketahui suku banyak f(x) = x³ – 2x² – x – 5. Nilai f(x) untuk x = 3 adalah…

Pembahasan:

Dalam contoh soal tipe ini, kamu bisa langsung menerapkan metode substitusi dengan memasukkan nilai x ke dalam persamaan. Berikut caranya:

f(x) = x³ – 2x² – x – 5

f(3) = 3³ – 2(3)² – 3 – 5

= 27 – 18  – 3 – 5 = 1

Jadi, nilai f(x) untuk x = 3 adalah 1.

Sudah Memahami Contoh Soal Suku Banyak?

Operasi hitung aljabar untuk suku banyak terdiri dari berbagai macam metode, baik penjumlahan, pengurangan, perkalian, dan pembagian. Pembagian suku banyak juga bisa kamu selesaikan menggunakan teorema sisa ataupun pembagian horner. Kamu bisa melihat berbagai contoh soal di atas untuk latihan soal seputar polinomial.