Apakah kamu pernah memperhatikan bagaimana suara merambat di udara, bagaimana gelombang air bergerak di permukaan, dan bagaimana cahaya menyebar dalam bentuk gelombang? Semua fenomena ini dapat dijelaskan dengan konsep gelombang berjalan.
Fenomena ini melibatkan perambatan energi melalui medium dalam bentuk gelombang. Jadi, dalam artikel ini, kita akan memperdalam materi tersebut, termasuk rumus-rumusnya, lalu memberikan beberapa contoh soal yang bermanfaat! Maka dari itu, simak penjelasan lengkapnya ya!
Apa Itu Gelombang Berjalan?
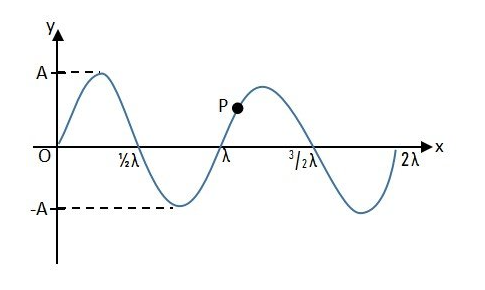
Gelombang berjalan adalah jenis gelombang, di mana energi gelombang terus bergerak maju melalui medium. Dalam gelombang ini, partikel medium mengalami getaran harmonik pada arah tegak lurus terhadap arah perambatan gelombang.
Konsep ini dapat diterapkan pada berbagai jenis gelombang, seperti gelombang suara, gelombang air, gelombang elektromagnetik, dan banyak lagi.
Pada dasarnya, gelombang ini terdiri dari tiga komponen utama, yaitu sumber energi, medium, dan perambatan energi gelombang itu sendiri.
Sumber energi menghasilkan getaran yang menggerakkan partikel dalam medium. Sehingga, partikel dalam medium saling berinteraksi dan menyebabkan energi gelombang ini pada medium dengan kecepatan tertentu.
Jika dijelaskan melalui contoh gelombang di permukaan air, maka ketika kita menjatuhkan batu ke dalam air, gelombang akan terbentuk dan menyebar keluar dari titik tumbukan.
Energi dari tumbukan batu menghasilkan getaran partikel air di sekitarnya. Getaran ini akan merambat melalui air, memindahkan energi gelombang dari satu tempat ke tempat lain.
Variabel-Variabel dalam Gelombang Berjalan
Ada beberapa variabel penting yang digunakan untuk menggambarkan gelombang ini dan memahami sifat serta perilakunya, seperti berikut:
1. Panjang Gelombang (λ)
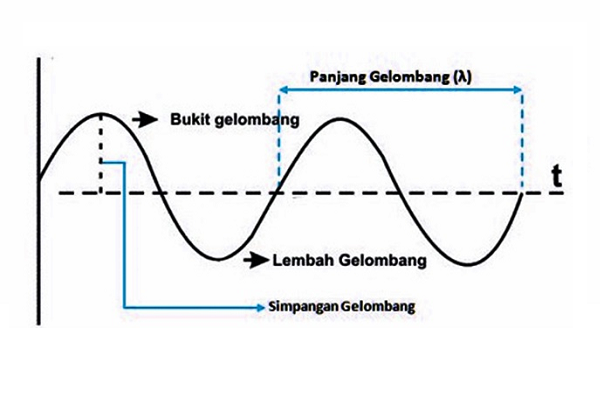
Panjang gelombang adalah jarak antara dua titik yang berdekatan pada gelombang, yang memiliki fase yang sama. Dapat diukur sebagai jarak antara dua puncak (atau lembah) berurutan dalam gelombang.
2. Cepat Rambat Gelombang (v)
Cepat rambat gelombang adalah jarak yang ditempuh oleh gelombang per satuan waktu dalam satuan meter per detik (m/s) dan ditentukan oleh sifat fisik medium, seperti kepadatan dan kelenturan.
3. Frekuensi Sudut (ω)
Frekuensi sudut adalah jumlah siklus gelombang yang terjadi dalam satu satuan waktu dan dihubungkan dengan frekuensi linier (f) dengan rumus ω = 2πf, di mana ω dinyatakan dalam radian per detik (rad/s). Fungsinya, yakni memberikan informasi tentang seberapa cepat gelombang melalui medium.
4. Frekuensi (f)
Frekuensi (f), yaitu jumlah siklus atau getaran yang terjadi dalam satu detik pada suatu gelombang dan diukur dalam satuan Hertz (Hz). Kamu bisa menghitungnya menggunakan rumus f = 1/T, dimana T adalah periode gelombang.
5. Periode (T)
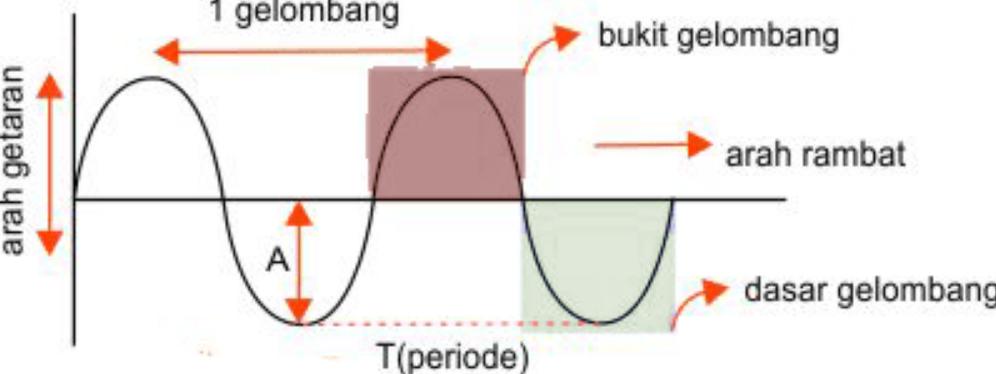
Lalu, periode adalah waktu yang dibutuhkan oleh satu siklus gelombang untuk melewati suatu titik.
Melalui penjelasan frekuensi di atas, maka kita tahu bahwa periode dan frekuensi saling terkait dengan rumus T= 1/f. Periode diukur dalam satuan detik (s) dan merupakan kebalikan dari frekuensi.
6. Simpangan (y)
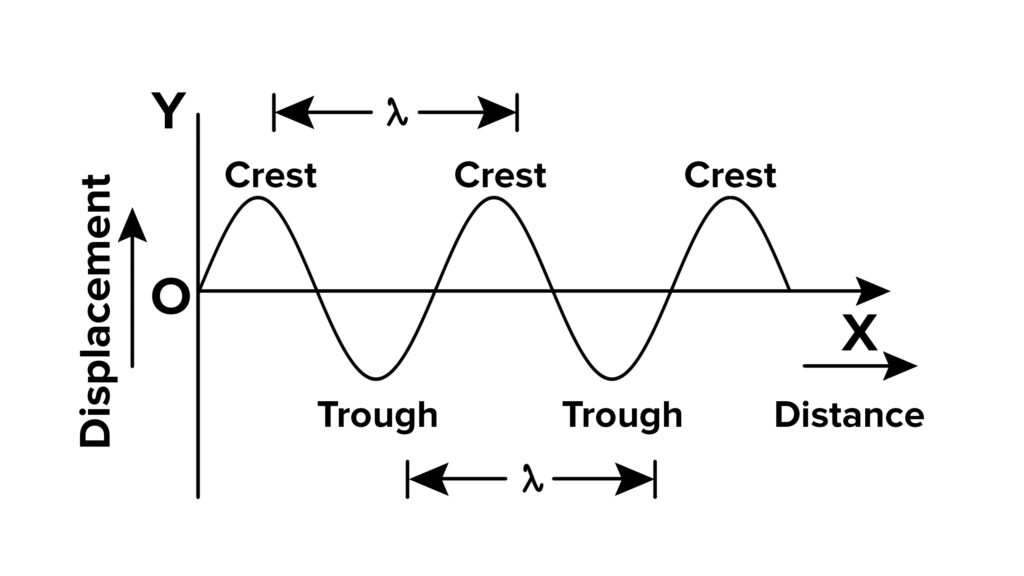
Kemudian terdapat simpangan, yaitu jarak maksimum yang ditempuh oleh partikel medium dari posisi keseimbangan saat gelombang berjalan melalui medium.
Jadi, simpangan memberikan ukuran dari seberapa jauh partikel-partikel medium bergeser dari posisi keseimbangan saat gelombang melintasinya. Simpangan dapat bervariasi, tergantung pada amplitudo gelombang.
7. Amplitudo (A)
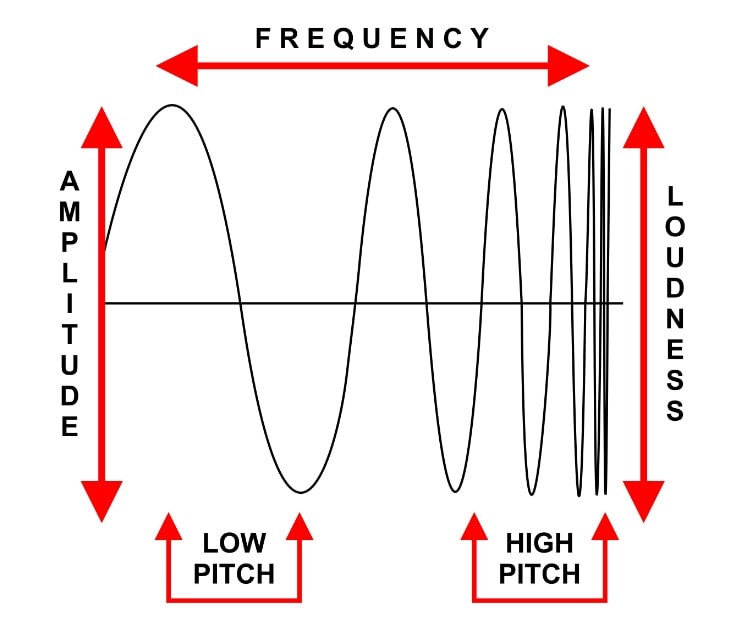
Sedangkan amplitudo adalah nilai maksimum simpangan gelombang, yaitu jarak dari posisi keseimbangan hingga titik tertinggi atau terendah dalam gelombang. Selain itu, amplitudo menjadi ukuran kekuatan atau intensitas gelombang dan memiliki hubungan dengan energi yang dibawa oleh gelombang tersebut.
8. Bilangan Gelombang (k)
Sementara bilangan gelombang adalah jumlah siklus gelombang dalam satu unit panjang atau biasanya dalam 1 meter. Jika bilangan gelombang (k) dihubungkan dengan panjang gelombang (λ), maka rumusnya yaitu k = 2π/λ.
Selain itu, bilangan gelombang memberikan informasi tentang seberapa sering gelombang berulang dalam jarak tertentu.
Bentuk Umum Rumus Gelombang Berjalan
Persamaan gelombang berjalan dinyatakan sebagai:
y(x, t) = (ωt – kx + φ)
- y adalah simpangan gelombang pada titik x dan waktu t.
- A adalah amplitudo gelombang, yaitu simpangan maksimum gelombang dari posisi keseimbangan.
- k adalah bilangan gelombang, yang menggambarkan jumlah siklus gelombang dalam satu satuan panjang.
- x adalah posisi titik pada gelombang.
- ω adalah frekuensi sudut, yang merupakan jumlah siklus gelombang yang terjadi dalam satu satuan waktu.
- t adalah waktu.
- φ adalah fase awal gelombang, yang menunjukkan posisi relatif gelombang pada suatu waktu tertentu.
Persamaan ini menggambarkan simpangan pada suatu titik (x) dan waktu (t). Selain itu, simpangan bergantung pada amplitudo, bilangan gelombang, frekuensi sudut, posisi, waktu, dan fase awal.
Namun, jika kita membuat asumsi bahwa t = 0 dan fase awal gelombangnya juga φ = 0, maka bentuk persamaan umum gelombang berjalan menjadi:
y(x, t) = (ωt – kx)
Rumus-Rumus Lainnya
Selain rumus umum di atas, terdapat beberapa rumus lain yang berhubungan, seperti berikut:
1. Rumus Panjang Gelombang
Panjang gelombang dinyatakan dalam satuan meter (m). Hubungan antara panjang gelombang, kecepatan rambat gelombang (v), dan frekuensi (f) dapat dinyatakan dengan rumus:
λ = v/f
Maka, rumus ini menunjukkan bahwa panjang gelombang adalah hasil bagi antara kecepatan rambat gelombang dan frekuensi. Dengan kata lain, semakin tinggi frekuensi gelombang, semakin pendek panjang gelombangnya, dan sebaliknya.
2. Rumus Cepat Rambat Gelombang
Sementara cepat rambat gelombang dinyatakan dalam satuan meter per detik (m/s). Hubungan antara cepat rambat gelombang, panjang gelombang (λ), dan frekuensi (f) dapat dinyatakan dengan rumus:
v = λf
Oleh karena itu, rumus ini menunjukkan bahwa cepat rambat gelombang adalah hasil kali antara panjang gelombang dan frekuensi. Dengan kata lain, semakin tinggi frekuensi gelombang, semakin cepat gelombang tersebut merambat melalui medium, dan sebaliknya.
Contoh Soal Gelombang Berjalan dan Pembahasannya
Baca bagian ini hingga selesai untuk memahami lebih dalam lagi materi ini dengan latihan beberapa contoh soal berkaitan dengan panjang gelombang. Selain itu, sudah kami sediakan juga pembahasannya untuk membantu pemahaman Anda:
1. Contoh Soal 1
Sebuah gelombang berjalan dengan amplitudo 0,1 m dan panjang gelombang 2 m. Hitunglah simpangan saat posisi gelombang berada pada x = 0,5 m.!
Jawaban:
Diketahui:
A = 0,1 m
λ = 2 m
x = 0,5 m
Rumus simpangan: y = A sin(kx)
k = 2π/λ= 2π/2= π
y = 0,1 sin (π * 0,5) = 0,1 sin (0,5π)= 0,1 m
Jadi, simpangan saat posisi gelombang berada pada x = 0,5 m adalah sekitar 0,1 m.
2. Contoh Soal 2
Jika terdapat persamaan gelombang y= 0,04 sin (10πt − 2πx) dengan t dalam satuan s, sedangkan y dan x dalam meter, maka carilah nilai:
a. amplitudo gelombang
b. frekuensi sudut gelombang
c. tetapan gelombang
d. cepat rambat gelombang
e. frekuensi gelombang
f. periode gelombang
g. panjang gelombang
h. simpangan, jika t = 1 s dan x = 1 m
Jawaban:
Kita tahu bahwa persamaan umum gelombang berjalan, yaitu y = A sin(ωt – kx) dengan A adalah amplitudo gelombang. Persamaan simpangan yang diberikan, yaitu y = 0,04 sin (10πt − 2πx).
Maka:
- A= 0,04 m
- Dari persamaan y= 0,04 sin (10πt − 2πx).
Maka, Frekuensi sudut gelombang (ω)= 10π rad/s.
- Dari persamaan y = 0,04 sin(10πt − 2πx).
Maka, nilai bilangan gelombang (k) = 2π.
- Cepat rambat gelombang, v= ω/k=10π/2π = 5 m/s.
- Rumus frekuensi sudut gelombang, ω = 2πf.
Maka, periode gelombang, f= ω/2π= 10π/2π = 5 Hz.
- Periode gelombang, T= 1/f = 1/ 5 = 0, 2 s.
- Rumus bilangan gelombang = k=2π/λ.
Maka, λ atau panjang gelombang= 2π/k= 2π/2π = 1 m.
- Simpangan, jika t= 1 s dan x= 1 m. Maka,
y = 0,02 sin(10πt − 2πx)
y = 0,02 sin(10 π (1) -2π (1))
y = 0,02 sin(10 π -2π)
y = 0,02 sin(8π)
y = 0,02 x 0
y = 0 m
Jadi, nilai simpangannya yaitu 0 m (terletak pada sumbu).
Sudah Paham dengan Gelombang Berjalan dan Rumusnya?
Dalam artikel ini, kita telah mendalami pengertian gelombang berjalan, sifat-sifatnya, variabel, serta berbagai rumus yang digunakan. Dengan pemahaman ini, kita dapat menerapkan konsep gelombang ini dalam memahami fenomena alam yang melibatkan gelombang.
Dari refraksi hingga interferensi, gelombang ini memainkan peran penting dalam ilmu pengetahuan dan teknologi. Penting juga untuk kamu ketahui, bahwa pengukuran gelombang tidak bisa secara manual, melainkan menggunakan alat, seperti Wave Gauge dan High Frequency Radar untuk mengukur gelombang laut.

