Gerak parabola merupakan salah satu konsep penting dalam fisika yang seringkali digunakan dalam berbagai bidang ilmu, seperti mekanika, matematika, dan ilmu kedirgantaraan. Istilah “parabola” merujuk pada suatu kurva geometris yang memiliki bentuk seperti huruf ‘U’.
Dalam gerak parabola, benda yang bergerak mengikuti lintasan yang membentuk parabola karena dipengaruhi oleh gaya gravitasi bumi. Dalam artikel ini, kita akan membahas pengertian, prinsip, serta rumus-rumus yang terkait dengan gerak parabola secara detail.
Pengertian Gerak Parabola
Gerak parabola adalah jenis gerakan benda di mana benda tersebut diluncurkan ke udara pada suatu sudut tertentu terhadap horizontal dan bergerak di bawah pengaruh gaya gravitasi bumi.
Dalam kondisi tanpa hambatan udara, lintasan gerak benda akan membentuk suatu parabola yang terbuka ke atas.
Contoh paling umum dari gerak parabola adalah gerakan benda yang dilempar ke udara tanpa adanya tenaga dorong tambahan setelah lemparan pertama. Misalnya, melempar bola ke atas dengan sudut tertentu, atau gerakan proyektil seperti peluru yang ditembakkan dari senjata api.
Prinsip Gerak Parabola
Gerak parabola didasarkan pada prinsip dasar gerakan benda jatuh bebas di bawah pengaruh gravitasi. Prinsip ini dinyatakan dalam Hukum II Newton, yaitu Hukum Gerak Newton, yang menyatakan bahwa gaya total yang bekerja pada suatu benda akan mengakibatkan percepatan pada benda tersebut.
Dalam kasus gerak parabola, gaya yang dominan adalah gaya gravitasi yang bekerja ke arah bawah.
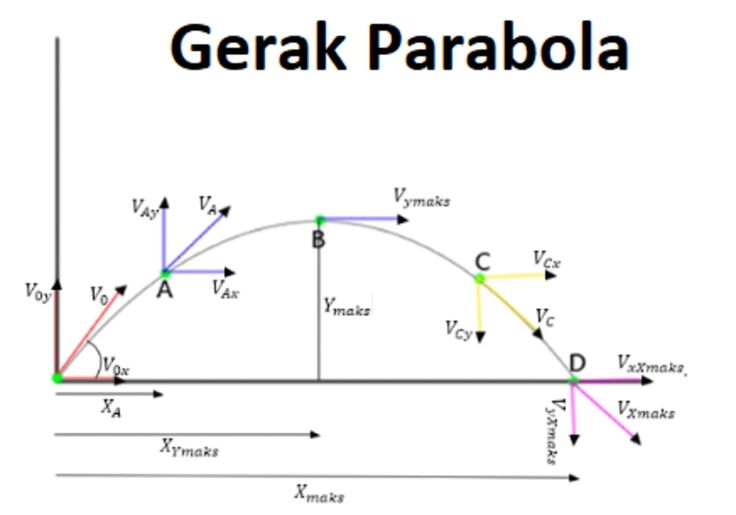
Ketika benda diluncurkan dengan kecepatan awal yang membentuk suatu sudut dengan horizontal, gerak benda akan memiliki dua komponen kecepatan, yaitu kecepatan horizontal dan kecepatan vertikal.
Kecepatan horizontal akan tetap konstan sepanjang perjalanan, karena gaya horizontalnya nol (diabaikan gesekan udara). Sementara itu, kecepatan vertikal akan mengalami perubahan karena pengaruh gravitasi.
Ketika kecepatan vertikal mencapai maksimum, benda akan berada di titik tertinggi gerakan parabolanya. Selanjutnya, kecepatan vertikal akan berkurang hingga mencapai nol saat benda mencapai tanah kembali.
Jadi, gerak parabola terdiri dari dua fase, yaitu fase naik (mengarah ke atas) dan fase turun (mengarah ke bawah).
Rumus-rumus Gerak Parabola
Dalam gerak parabola, terdapat beberapa rumus penting yang digunakan untuk menghitung berbagai parameter gerakan benda. Beberapa rumus tersebut adalah:
1. Komponen Kecepatan
Kecepatan benda yang dilempar dapat dinyatakan sebagai vektor dengan dua komponen: kecepatan horizontal (v₀x) dan kecepatan vertikal (v₀y). Kecepatan horizontal tetap konstan, sedangkan kecepatan vertikal akan berubah akibat gaya gravitasi.
Rumus untuk kedua komponen kecepatan ini adalah:
V₀x = V₀ cos(θ)
V₀y = V₀ sin(θ)
di mana:
v₀ = kecepatan awal (kecepatan total pada saat lemparan pertama),
θ = sudut lemparan terhadap horizontal.
2. Waktu Puncak (T₀)
Waktu yang diperlukan oleh benda untuk mencapai titik tertinggi (puncak) dari gerak parabola dapat dihitung menggunakan rumus:
T₀ = V₀y
2
di mana:
g = percepatan gravitasi bumi (biasanya sekitar 9,8 m/s²).
3. Ketinggian Maksimum (H)
Ketinggian maksimum yang dapat dicapai oleh benda dapat dihitung menggunakan rumus:
H = V₀y²
2g
4. Jarak Horizontal Maksimum (R)
Jarak horizontal maksimum yang ditempuh oleh benda sebelum mencapai permukaan tanah kembali dapat dihitung menggunakan rumus:
R = V₀x 2V₀y
g
5. Waktu Total Penerbangan (T)
Waktu total yang diperlukan benda untuk mencapai tanah kembali setelah diluncurkan dapat dihitung sebagai dua kali waktu puncak (naik dan turun), yaitu:
T = 2 T₀ = 2V₀y
g
Contoh Soal & Pembahasan Gerak Parabola
Berikut ini adalah contoh soal sederhana mengenai gerak parabola beserta pembahasannya:
Soal 1:
Sebuah bola dilempar dengan kecepatan awal sebesar 15 m/s membentuk sudut 30 derajat terhadap horizontal. Hitunglah waktu yang diperlukan bola untuk mencapai titik tertinggi gerak parabolanya (waktu puncak).
Jawaban:
Kita dapat menggunakan rumus waktu puncak (T₀) untuk menghitung waktu yang diperlukan bola untuk mencapai titik tertinggi.
Diketahui:
v₀ = 15 m/s (kecepatan awal)
θ = 30° (sudut lemparan terhadap horizontal)
g = 9,8 m/s² (percepatan gravitasi bumi)
Langkah-langkah perhitungan:
1. Hitung komponen kecepatan vertikal (v₀y):
v₀y = v₀ * sin(θ)
v₀y = 15 m/s * sin(30°)
v₀y = 7,5 m/s
2. Hitung waktu puncak (T₀):
T₀ = v₀y / g
T₀ = 7,5 m/s / 9,8 m/s²
T₀ = 0,765 s
Jadi, waktu yang diperlukan bola untuk mencapai titik tertinggi gerak parabolanya adalah sekitar 0,765 detik.
Soal 2:
Sebuah batu dilemparkan secara horizontal dari ketinggian 20 meter di atas tanah dengan kecepatan 10 m/s. Berapa jarak horizontal yang ditempuh batu sebelum mencapai tanah kembali?
Jawaban:
Kita dapat menggunakan rumus untuk jarak horizontal maksimum (R) untuk menghitung jarak yang ditempuh batu sebelum mencapai tanah kembali.
Diketahui:
v₀x = 10 m/s (kecepatan horizontal, karena diluncurkan secara horizontal)
v₀y = 0 m/s (kecepatan vertikal pada saat lemparan horizontal)
g = 9,8 m/s² (percepatan gravitasi bumi)
H = 20 m (ketinggian awal)
Langkah-langkah perhitungan:
1. Hitung waktu total penerbangan (T):
T = 2 * T₀ (karena batu akan kembali ke tinggi awal)
T = 2 * (v₀y / g) = 2 * (0 m/s / 9,8 m/s²) = 0 s
2. Hitung jarak horizontal maksimum (R):
R = v₀x * T = 10 m/s * 0 s = 0 m
Jadi, jarak horizontal yang ditempuh batu sebelum mencapai tanah kembali adalah 0 meter. Hal ini karena batu dilemparkan secara horizontal tanpa adanya komponen kecepatan vertikal.
Soal 3:
Rudal diluncurkan dengan kecepatan awal 50 m/s pada sudut 60 derajat terhadap horizontal. Berapa ketinggian maksimum yang dapat dicapai roket?
Jawaban:
Kita dapat menggunakan rumus untuk ketinggian maksimum (H) untuk menghitung ketinggian maksimum yang dapat dicapai roket.
Diketahui:
v₀ = 50 m/s (kecepatan awal)
θ = 60° (sudut lemparan terhadap horizontal)
g = 9,8 m/s² (percepatan gravitasi bumi)
Langkah-langkah perhitungan:
1. Hitung komponen kecepatan vertikal (v₀y):
v₀y = v₀ * sin(θ)
v₀y = 50 m/s * sin(60°)
v₀y = 43,30 m/s
2. Hitung ketinggian maksimum (H):
H = (V₀y²) / (2 g)
H = (43,30 m/s)² / (2 9,8 m/s²)
H = 939,34 m
Jadi, ketinggian maksimum yang dapat dicapai roket adalah sekitar 939,34 meter.
Contoh Gerak Parabola di Kehidupan Sehari-hari
Gerak parabola adalah fenomena gerak benda yang sering kita temui dalam kehidupan sehari-hari. Berikut adalah beberapa contoh gerak parabola yang dapat kita amati:
1. Melempar Bola
Ketika seseorang melempar bola ke atas dengan suatu sudut tertentu terhadap horizontal, bola tersebut akan mengikuti gerak parabola. Bola akan mencapai titik tertinggi pada lintasan dan kemudian kembali ke tanah dengan mengikuti parabola.
2. Terjun Bebas
Saat seseorang melakukan terjun bebas dari ketinggian tertentu, gerakan yang diikuti akan berupa gerak parabola. Awalnya, terjun bebas memiliki kecepatan vertikal nol, kemudian kecepatan meningkat karena gaya gravitasi, mencapai titik tercepat saat mendekati tanah.
3. Meluncurkan Pesawat Kertas
Apabila seseorang meluncurkan pesawat kertas, pesawat tersebut akan mengikuti gerak parabola. Lintasan pesawat akan membentuk suatu parabola, naik ke atas, mencapai titik tertinggi, dan turun kembali ke tanah.
4. Menyiram Tanaman dengan Selang Air
Saat tukang kebun menyiram tanaman dengan selang air, air yang keluar dari ujung selang akan membentuk gerak parabola sebelum mencapai tanah. Lintasan parabola air dapat keluar dari selang tersebut.
Contoh-contoh di atas menggambarkan bagaimana gerak parabola adalah fenomena yang umum terjadi dalam berbagai aspek kehidupan sehari-hari dan sangat relevan dalam pemahaman fisika dan matematika.
Ternyata Gerak Parabola Sering Terjadi di Sekitar Kita, Bukan?
Gerak parabola adalah fenomena gerak benda yang diakibatkan oleh pengaruh gravitasi bumi dan kecepatan awal yang membentuk sudut tertentu terhadap horizontal.
Lintasan gerak benda membentuk suatu parabola yang terbuka ke atas. Prinsip gerak parabola didasarkan pada hukum gerak Newton, di mana gaya gravitasi adalah gaya dominan yang bekerja pada benda.
Dengan menguasai konsep ini, kita dapat lebih memahami dan memprediksi pergerakan benda dalam berbagai situasi, serta mengoptimalkan berbagai aspek perancangan dan perhitungan terkait gerak parabola.

