Pertidaksamaan adalah salah satu konsep matematika yang melibatkan perbandingan hubungan antara dua ekspresi atau angka. Nah, memahami himpunan penyelesaian pertidaksamaan dan cara menentukan solusinya adalah kunci untuk keberhasilan dalam matematika dan banyak bidang lainnya.
Dalam artikel ini, Anda bisa menjelajahi dasar-dasar himpunan penyelesaian pertidaksamaan. Dengan pemahaman yang mendalam tentang metode-metode efektif dan contoh-contoh praktisnya, Anda akan dapat menghadapi pertidaksamaan dengan percaya diri dan mencapai solusi yang akurat.
Apa Itu Pertidaksamaan?
Pertidaksamaan adalah istilah matematika yang melibatkan satu atau lebih variabel dan menggunakan tanda ketidaksamaan (<, >, ≤, atau ≥). Pertidaksamaan bentuk linear tidak mengandung fungsi polinomial, trigonometri, logaritma, atau eksponensial.
Pertidaksamaan linear memiliki dua sifat penting yang dapat membantu Anda dalam memahaminya dan memanipulasinya. Pertama, sebuah pertidaksamaan akan tetap memiliki nilai yang sama jika kedua ruasnya ditambahkan atau dikurangkan dengan bilangan yang sama.
Misalnya, jika Anda menambahkan bilangan 5 pada kedua ruas pertidaksamaan, maka nilai pertidaksamaan tetap tidak berubah. Sifat ini memungkinkan Anda untuk melakukan operasi matematika yang sama pada kedua ruas pertidaksamaan tanpa mengubah kebenarannya.
Sifat kedua pertidaksamaan linear adalah ketidakberubahannya jika kedua ruasnya dikalikan atau dibagi dengan bilangan positif yang sama. Dalam hal ini, Anda dapat mengalikan atau membagi kedua ruas dengan bilangan positif, dan nilai pertidaksamaan tetap tidak berubah.
Misalnya, jika Anda membagi kedua ruas dengan 2, maka pertidaksamaan masih memiliki nilai yang sama. Sifat ini memungkinkan Anda untuk menyederhanakan pertidaksamaan dengan mengalikan atau membaginya dengan bilangan yang memudahkan analisis.
Dengan memahami sifat-sifat ini, Anda dapat memanipulasi pertidaksamaan linear dengan lebih mudah dan akurat. Hal ini sangat penting dalam pemecahan masalah matematika, ilmu ekonomi, ilmu fisika, dan banyak bidang lainnya.
Tentunya dengan kondisi bahwa pertidaksamaan linear berguna untuk menggambarkan hubungan antara variabel-variabel yang terlibat. Dengan keterampilan ini, Anda dapat mengidentifikasi himpunan penyelesaian pertidaksamaan, menggambarkan grafiknya, dan menerapkannya secara nyata.
Apa Itu Himpunan Penyelesaian Pertidaksamaan?

Pertidaksamaan linear memiliki sifat khusus yang memungkinkan Anda untuk menentukan himpunan penyelesaian pertidaksamaan dengan tepat. Apakah itu?
Himpunan penyelesaian pertidaksamaan linear merupakan irisan dari himpunan penyelesaian masing-masing pertidaksamaan linearnya. Dalam pertidaksamaan linear, terdapat situasi khusus ketika kedua ruas dikalikan atau dibagi dengan bilangan negatif (-).
Pada kasus ini, tanda ketidaksamaan akan berubah menjadi tanda sebaliknya yang berbeda dari tanda sebelumnya. Misalnya, jika dalam pertidaksamaan Anda memiliki -6x + 2 < 20, maka dengan mengalikan kedua ruas dengan -1 (bilangan negatif) tanda ketidaksamaan berubah menjadi >, sehingga menjadi -6x > -18.
Perubahan ini penting untuk memastikan kebenaran pertidaksamaan dalam konteks matematika yang konsisten. Proses menentukan himpunan pertidaksamaan ini dapat Anda terapkan pada persamaan satu variabel maupun dua variabel. Setelah ini, Anda akan membahasnya lebih dalam dan lengkap.
Langkah-langkah yang perlu Anda lakukan ialah mengidentifikasi variabel yang terlibat dalam himpunan pertidaksamaan. Lalu, mengisolasi variabel tersebut pada satu ruas dan mengevaluasi ketidaksamaan dengan memperhatikan perubahan tanda jika ada operasi perkalian atau pembagian dengan bilangan negatif.
Jenis Himpunan Penyelesaian Pertidaksamaan
Pertidaksamaan linear dapat Anda gunakan untuk memecahkan masalah sehari-hari ketika terkonversi ke dalam model matematika. Mari kita eksplorasi jenis-jenis pertidaksamaan linear berikut ini:
1. Pertidaksamaan Linear Satu Variabel
Pertidaksamaan linear satu variabel adalah suatu bentuk pertidaksamaan yang melibatkan hanya satu variabel di mana pangkat tertinggi adalah satu (linear). Bentuk umum dari pertidaksamaan linear satu variabel dapat dituliskan sebagai:
- ax + b > c
- ax + b < c
- ax + b ≥ c
- ax + b ≤ c
Pada persamaan di atas, a merupakan koefisien variabel x, x adalah variabel itu sendiri, sedangkan b dan c adalah konstanta. Kemudian tanda <, >, ≤, atau ≥ menunjukkan ketidaksamaan yang berlaku.
Misalnya, pertidaksamaan linear satu variabel “2x + 3 > 5” menyatakan bahwa hasil penjumlahan 2x dan 3 harus lebih besar dari 5. Pertidaksamaan ini dapat Anda gunakan untuk menemukan nilai x yang memenuhi syarat tersebut.
Dengan memahami bentuk umum dan konsep pertidaksamaan linear satu variabel, Anda dapat menerapkannya dalam berbagai situasi dalam kehidupan sehari-hari. Misalnya, dalam perencanaan anggaran, Anda dapat menggunakan konsep tersebut untuk memodelkan batasan pengeluaran berdasarkan pendapatan yang tersedia.
Dengan menganalisis dan menyelesaikan himpunan penyelesaian pertidaksamaan tersebut, Anda dapat mengidentifikasi kisaran nilai yang memenuhi persyaratan yang ditentukan. Mudah, bukan?
2. Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel adalah bentuk pertidaksamaan yang melibatkan dua variabel di mana pangkat tertinggi variabel tersebut adalah satu. Bentuk umum dari pertidaksamaan linear dua variabel dapat dituliskan sebagai:
- ax + by > c
- ax + by < c
- ax + by ≥ c
- ax + by ≤ c
Dalam persamaan tersebut, x dan y merupakan variabel-variabel yang terlibat, a dan b adalah koefisien dari masing-masing variabel, dan c adalah konstanta. Tanda <, >, ≤, atau ≥ menunjukkan ketidaksamaan yang berlaku.
Misalnya, pertidaksamaan linear dua variabel “2x + 3y > 5” menyatakan bahwa hasil penjumlahan 2x dan 3y harus lebih besar dari 5. Pertidaksamaan ini berguna untuk mencari kombinasi nilai x dan y yang memenuhi syarat tersebut.
Dalam pertidaksamaan linear dua variabel, ada juga peraturan khusus ketika kedua ruas dikalikan atau dibagi dengan bilangan negatif (-). Dalam kasus ini, tanda ketidaksamaan akan berubah menjadi tanda sebaliknya yang berbeda dari tanda sebelumnya.
Misalnya, jika terdapat pertidaksamaan -6x + 2 < 20, dengan mengalikan kedua ruas dengan -1 (bilangan negatif), maka tanda ketidaksamaan berubah menjadi > dan berubah menjadi -6x > -18. Perubahan ini penting untuk menjaga konsistensi matematika dalam pertidaksamaan.
Dengan memahami bentuk dan konsep pertidaksamaan linear dua variabel, Anda bisa menerapkannya dalam berbagai situasi dalam kehidupan sehari-hari. Misalnya, dalam analisis ekonomi, Anda dapat menggunakan pertidaksamaan ini untuk memodelkan hubungan antara dua variabel ekonomi seperti harga dan permintaan.
Dengan menyelesaikan himpunan penyelesaian pertidaksamaan tersebut, Anda dapat mengidentifikasi kombinasi nilai x dan y yang memenuhi persyaratan yang ditetapkan.
Cara Menentukan dan Contoh Soal Himpunan Penyelesaian Pertidaksamaan
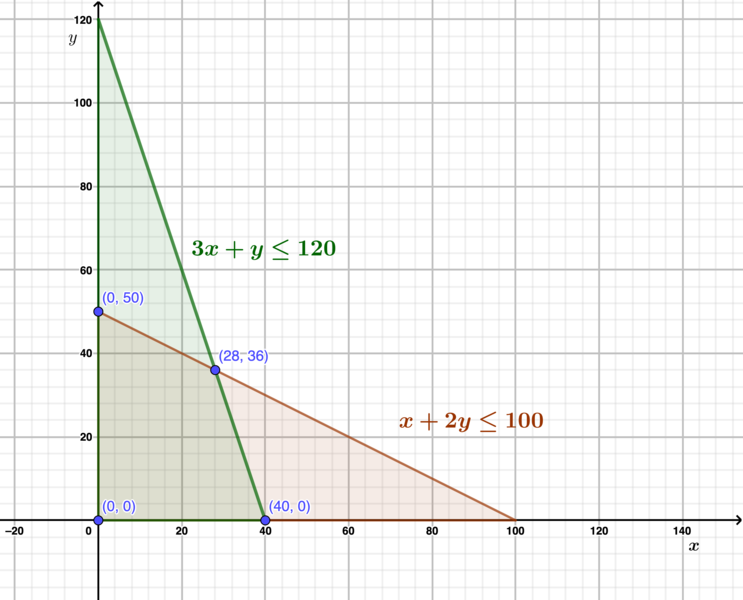
Berikut ini adalah beberapa contoh-contoh soalnya:
1. Contoh 1
Temukan himpunan penyelesaian dari dua bentuk pertidaksamaan berikut ini!
4 – 3x ≥ 4x + 18 (pertidaksamaan 1); 8x + 1 < x – 20 (pertidaksamaan 2),
Pembahasan:
Dalam pertidaksamaan pertama, yaitu 4 – 3x ≥ 4x + 18, dapat dihitung bahwa:
-4x – 3x ≥ −4 + 18
−7x ≥ 14
x ≤ −2
Setelah melakukan langkah-langkah penyelesaian yang telah diberikan, diperoleh HP (Himpunan Penyelesaian) berupa {x | x ≤ −2, x ∈ R}. Ini berarti bahwa himpunan nilai x yang memenuhi pertidaksamaan tersebut adalah semua nilai x yang kurang dari atau sama dengan -2, dan x adalah bilangan real.
Sedangkan dalam pertidaksamaan kedua, yaitu 8x + 1 < x – 20, dapat dihitung bahwa:
8x – x < −20 – 1
7x < −21
x < −3
Setelah melakukan langkah-langkah penyelesaian yang telah diberikan, diperoleh HP berupa {x | x < −3, x ∈ R}. Ini berarti bahwa himpunan penyelesaian pertidaksamaan nilai x yang memenuhi pertidaksamaan tersebut adalah semua nilai x yang kurang dari -3, dan x adalah bilangan real.
Dalam kedua kasus tersebut, HP memberikan informasi tentang himpunan nilai x yang memenuhi pertidaksamaan yang diberikan. Dalam notasi set, {x | …} menyatakan himpunan semua nilai x yang memenuhi kondisi tertentu.
2. Contoh 2
Temukan himpunan penyelesaian pertidaksamaan dari 4x + 8y ≥ 16!
Pembahasan:
HP dari pertidaksamaan 4x + 8y ≥ 16
Mencari x (y = 0):
4x = 16
x = 16/4
x = 4
Mencari y (x = 0):
8y = 16
y = 16/8
y = 2
Kesimpulan HP nya adalah (x, y) = (4, 2). Ini berarti bahwa semua pasangan nilai x dan y yang memenuhi pertidaksamaan tersebut adalah ketika x = 4 dan y = 2. Dalam hal ini, x harus lebih besar atau sama dengan 4 dan y harus lebih besar atau sama dengan 2 agar pertidaksamaan terpenuhi.
Baca Juga : Definisi Himpunan, Cara Menyatakan, Jenis, dan Contoh Soalnya
Sudah Paham dengan Konsep Himpunan Penyelesain Pertidaksamaan?
Dalam memahami pertidaksamaan dan himpunan penyelesaiannya, penting untuk menguasai langkah-langkah penyelesaian yang tepat. Himpunan penyelesaian pertidaksamaan adalah himpunan nilai yang memenuhi pertidaksamaan tersebut.
Dengan pemahaman ini, Anda dapat menganalisis hubungan matematika dengan lebih baik. Kemudian juga mengaplikasikannya dalam berbagai situasi kehidupan sehari-hari. Saat belajar, buat catatan tentang konsep-konsep kunci dan teknik-teknik yang Anda pelajari.
Jika memungkinkan, gunakan grafik atau diagram untuk memvisualisasikan pertidaksamaan. Cara ini dapat membantu Anda melihat himpunan penyelesaian dengan lebih jelas. Selamat belajar!

