Dalam usaha untuk mengungkap dan memahami fenomena tentang pergerakan benda langit yang mengelilingi Matahari, seorang astronom dan matematikawan brilian bernama Johannes Kepler menemukan tiga hukum penting pada abad ke-17. Hukum-hukum ini dikenal sebagai Hukum Kepler
Pengertian Hukum Kepler
Hukum Kepler adalah rangkaian tiga prinsip fundamental yang menggambarkan gerakan planet di sekitar matahari. Meski usianya sudah berabad-abad, hukum-hukum ini masih menjadi dasar bagi pemahaman modern tentang gerakan planet dan objek bergerak di tata surya. Berikut ini adalah penjelasan lengkapnya.
Hukum I Kepler (Hukum Orbit)
Hukum I Kepler menyatakan bahwa setiap planet mengelilingi Matahari dalam jalur berbentuk elips. Di dalam elips ini, Matahari berada di salah satu fokusnya, bukan di pusatnya seperti yang sering kita bayangkan.
Artinya, planet-planet tidak bergerak dalam lingkaran sempurna mengelilingi Matahari, melainkan dalam bentuk lonjong seperti elips. Hukum kepler ini bisa dianalogikan seperti kamu menarik tali di ujungnya sehingga membentuk lingkaran, tapi tali itu tidak benar-benar kencang dan dapat bergeser.
Ketika tali bergerak dari pusatnya, maka akan membentuk elips, dan Matahari berada di salah satu titik penting dalam bentuk elips ini. Adapun bunyi dan rumus dari hukum orbit adalah sebagai berikut:
1. Bunyi Hukum I Kepler
“Benda langit yang mengelilingi Matahari bergerak dalam orbit elips, di mana Matahari berada pada salah satu fokusnya (elips memiliki dua titik fokus)”.
2. Rumus Hukum I Kepler
Rumus Hukum Kepler Pertama tidak melibatkan persamaan matematika yang spesifik. Namun, bentuk umum dari elips adalah sebagai berikut:
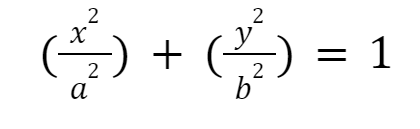
Dalam persamaan di atas:
- x dan y = koordinat posisi sebuah planet di orbit elips.
- a = setengah panjang sumbu mayor elips, yaitu jarak dari pusat elips ke tepi terjauh elips.
- b = setengah panjang sumbu minor elips, yaitu jarak dari pusat elips ke tepi terdekat elips.
Hukum II Kepler (Hukum Luas)
Hukum II Kepler menyatakan bahwa saat sebuah planet bergerak mengelilingi Matahari, planet tersebut akan mengitari luas yang sama dalam waktu yang sama. Dengan kata lain, jika kamu menggambar garis dari planet ke Matahari, wilayah yang dilalui oleh garis ini akan memiliki luas sama setiap periode waktu yang sama.
Hukum kepler ini bisa dianalogikan seperti kamu sedang mengayuh sepeda di sekitar lapangan olahraga yang berbentuk elips.
Waktu yang kamu butuhkan untuk menyelesaikan satu putaran lapangan (periode) adalah sama, apakah kamu sedang di dekat garis tengah atau di ujung elips. Sehingga, wilayah yang kamu lalui dengan mengayuh sepeda memiliki luas yang sama dalam waktu yang sama. Berikut adalah bunyi dan Hukum Luas, antara lain:
1. Bunyi Hukum II Kepler
“Gariskan dari sebuah benda langit ke Matahari akan menyapu luas yang sama dalam waktu yang sama, selama benda langit tersebut bergerak mengelilingi Matahari.”
2. Rumus Hukum II Kepler
Rumus Hukum Kepler Kedua tidak melibatkan persamaan matematika, tetapi dapat dijelaskan dalam bentuk pernyataan sebagai berikut:
“Dalam waktu yang sama, garis yang menghubungkan sebuah planet dengan Matahari akan menyapu luas yang sama saat planet bergerak mengelilingi Matahari.”
Artinya, saat planet berada lebih dekat ke Matahari (perihelion) dan bergerak lebih cepat, garis yang menghubungkannya dengan Matahari akan menyapu luas yang sama dalam waktu yang sama dibandingkan dengan saat planet berada lebih jauh dari Matahari (aphelion) dan bergerak lebih lambat.
Jika waktu yang dibutuhkan sebuah planet untuk bergerak dari titik A ke B sama dengan waktu yang dibutuhkan untuk bergerak dari titik C ke D, dan juga sama dengan waktu yang dibutuhkan untuk bergerak dari titik E ke F, maka luas AMB=CMD=EMF.
Hukum III Kepler (Hukum Periode)
Hukum III Kepler menjelaskan hubungan antara periode (waktu yang dibutuhkan sebuah planet untuk mengorbit Matahari satu kali) dengan jarak rata-rata planet tersebut dari Matahari. Selain itu, hukum ini menyatakan bahwa semakin jauh sebuah planet dari Matahari, semakin lama periode orbitnya.
Selain itu, Hukum III Kepler juga berlaku untuk semua planet di tata surya, artinya, hubungan ini berlaku untuk semua planet yang mengelilingi Matahari.
Untuk membayangkan Hukum kepler ini, mari kita bandingkan berlari di jalur lingkaran dengan berlari di jalur elips yang berbeda-beda. Saat kamu berlari di lingkaran lebih dekat ke tengah, jarak yang harus ditempuh lebih pendek dan kamu akan lebih cepat mencapai garis start kembali (periode yang lebih pendek).
Namun, jika kamu berlari di jalur elips yang lebih jauh dari tengah, jarak yang harus ditempuh lebih panjang dan kamu akan lebih lama mencapai garis start kembali (periode yang lebih lama). Berikut adalah bunyi dan rumus Hukum III Kepler, antara lain:
1. Bunyi Hukum III Kepler
“Kuadrat periode dari sebuah benda langit yang mengorbit Matahari berbanding lurus dengan kubus jarak rata-rata benda langit tersebut dari Matahari.”
2. Rumus Hukum III Kepler
Rumus Hukum Kepler Ketiga menyatakan hubungan antara periode orbit (T) dan jarak rata-rata dari Matahari (R) bagi sebuah planet. Rumusnya adalah sebagai berikut:
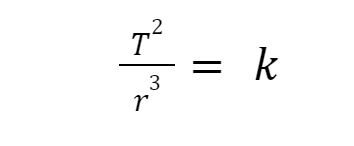
- T = periode planet mengelilingi Matahari
- r = jarak rata-rata planet dari Matahari
- K = bilangan konstan yang nilainya sama untuk setiap planet di tata surya kita
Persamaan hukum III Kepler di atas dapat juga dinyatakan sebagai:
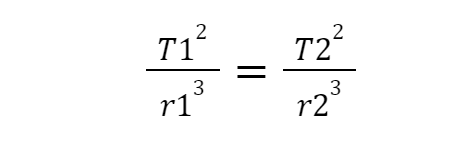
- T1 = periode planet I
- T2 = periode planet II
- r1 = jarak rata-rata planet I ke Matahari
- r2 = jarak rata-rata planet II ke Matahari
Contoh soal Hukum Kepler
Agar bisa lebih mudah memahami Hukum Kepler, berikut ini tersedia beberapa contoh soal beserta pembahasannya. Silakan diamati dan asah terus pemahaman Anda terkait prinsip yang sangat penting bagi ilmu astronomi modern ini.
1. Soal Pertama
Planet X mengorbit Matahari dalam lintasan elips dengan setengah panjang sumbu mayor (a) sebesar 3 AU (satuan astronomi) dan setengah panjang sumbu minor (b) sebesar 2 AU. Di mana posisi Matahari berada?
Pembahasan 1:
Dalam Hukum Kepler Pertama, diketahui bahwa Matahari berada di salah satu fokus elips. Setengah panjang sumbu mayor (a) adalah jarak dari pusat elips ke tepi terjauh elips, dan setengah panjang sumbu minor (b) adalah jarak dari pusat elips ke tepi terdekat elips. Jadi, Matahari berada pada salah satu titik fokus elips.
2. Soal Kedua
Planet Z mengorbit Matahari dalam lintasan elips dengan setengah panjang sumbu mayor (a) sebesar 10 juta kilometer dan periode orbit (T) selama 2 tahun. Hitunglah setengah panjang sumbu minor (b) dari lintasan planet Z.
Pembahasan 3:
Dalam Hukum Kepler Ketiga, kita tahu bahwa (T^2 / R^3) adalah konstanta. Kita dapat menggunakan konstanta ini untuk mencari R (jarak rata-rata planet Z dari Matahari).
T = 2 tahun
R =?
(T)^2 = (R)^3 x (konstanta)
(2 tahun)^2 = (R)^3 x (konstanta)
4 tahun^2 = (R)^3 x (konstanta)
R^3 = 4 tahun^2 / konstanta
R ≈ akar pangkat tiga dari (4 tahun^2 / konstanta)
Setelah mendapatkan nilai R, kita dapat menghitung setengah panjang sumbu minor (b) menggunakan persamaan elips.
b ≈ akar dari (a^2 – R^2)
b ≈ akar dari (10 juta kilometer)^2 – (R)^2
Jadi, dengan menghitung R dan b, kita akan mendapatkan nilai setengah panjang sumbu minor (b) dari lintasan planet Z.
3. Soal Ketiga
Planet C mengorbit Matahari dalam lintasan elips. Jarak dari planet C ke Matahari saat berada di perihelion adalah 80 juta kilometer, sementara saat berada di aphelion adalah 120 juta kilometer. Hitunglah eksentrisitas (e) lintasan orbit planet C.
Pembahasan 4:
Eksentrisitas (e) adalah ukuran seberapa elips lintasan orbit planet. Eksentrisitas dapat dihitung dengan rumus:
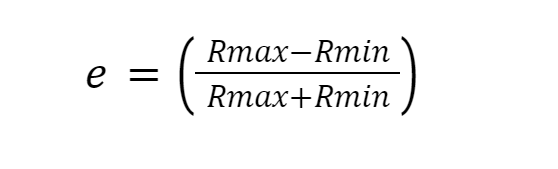
- Rmax = jarak dari planet ke Matahari saat berada di aphelion (jarak terjauh).
- Rmin = jarak dari planet ke Matahari saat berada di perihelion (jarak terdekat).
Dalam contoh ini, kita telah diberikan nilai Rmax dan Rmin:
Rmax = 120 juta kilometer
Rmin = 80 juta kilometer
Sekarang, kita dapat menghitung eksentrisitas (e):
e = (120 juta kilometer – 80 juta kilometer) / (120 juta kilometer + 80 juta kilometer)
e = 40 juta kilometer / 200 juta kilometer
Jadi, e = 0.2
Jadi, eksentrisitas lintasan orbit planet C adalah 0.2 atau 20%.
Semakin mendekati nilai 0, lintasan semakin mendekati bentuk lingkaran, dan semakin mendekati nilai 1, lintasan semakin mendekati bentuk elips yang sangat pipih.
Sudah Tahu Rumus dari Hukum Kepler?
Nah, itu dia penjelasan lengkap terkait rumus hukum kepler. Mulai dari hukum kepler 1, 2, hingga 3, bisa Anda pelajari dengan seksama melalui penjelasan di dalam artikel ini. Melalui ketiga hukum tersebut, kita dibawa untuk memahami struktur dan perilaku tata surya secara lebih dalam lagi.