Pada pelajaran matematika, setidaknya kita pasti pernah menemui materi tentang pembuktian suatu rumus. Dengan membuktikan rumus, kita diharapkan dapat lebih memahami konsep matematika dengan tepat. Salah satu cara untuk membuktikan rumus yaitu dengan menggunakan induksi matematika.
Tetapi, apakah induksi matematika itu? Berikut penjelasan lengkap beserta langkah-langkah penyelesaian dan contoh soalnya.
Pengertian
Induksi matematika adalah suatu metode dalam matematika untuk membuktikan kebenaran pernyataan atau sifat matematika pada semua bilangan bulat positif (biasanya dimulai dari bilangan 1). Metode ini didasarkan pada dua langkah utama, yaitu kasus dasar dan langkah induksi.
Metode induksi matematika sangat berguna dalam membuktikan banyak pernyataan matematika, seperti sifat pola, deret matematika, ketaksamaan, dan sebagainya. Selain itu, metode ini tetap menjadi alat penting dalam memecahkan berbagai masalah di berbagai cabang matematika.
Efek Domino dalam Induksi Matematika
Istilah “efek domino” dalam konteks induksi matematis mengacu pada konsep bahwa sekali pernyataan atau sifat matematika telah dibuktikan benar untuk suatu nilai kasus dasar dan untuk suatu nilai k, maka pernyataan tersebut otomatis juga benar untuk semua nilai yang lebih besar dari k.
Dengan demikian, setiap “domino” (pernyataan) yang telah jatuh (terbukti benar untuk suatu nilai) akan menyebabkan “domino” berikutnya (nilai berikutnya) juga jatuh atau terbukti benar. Proses ini berlanjut tanpa batas untuk setiap bilangan bulat non-negatif yang lebih besar dari nilai kasus dasar.
Inilah sebabnya metode induksi matematis sering dijelaskan sebagai “efek domino”, karena sekali kita membuktikan pernyataan untuk kasus dasar dan menunjukkan itu benar untuk suatu nilai k, maka itu juga benar untuk k + 1. Artinya, pernyataan tersebut otomatis benar untuk semua nilai yang lebih besar dari k.
Rumus
Rumus induksi matematika adalah sebuah metode yang digunakan untuk membuktikan kebenaran pernyataan atau properti yang berlaku untuk semua bilangan bulat non-negatif. Berikut rumus yang dapat diaplikasikan dalam menentukan induksi matematika:
n = 1 untuk menyatakan pernyataan yang benar.
n= k untuk menduga pernyataan benar.
n = k+1 untuk menyatakan pernyataan benar
Prinsip
Prinsip induksi matematis adalah sebuah prinsip dasar dalam matematika yang digunakan untuk membuktikan pernyataan yang berlaku untuk semua bilangan bulat non-negatif (atau sejumlah tak hingga bilangan bulat). Prinsip ini merupakan dasar dari metode induksi matematis yang telah dijelaskan sebelumnya.
Prinsip induksi matematika menyatakan bahwa jika suatu pernyataan benar untuk kasus dasar (biasanya n = 0 atau n = 1) dan jika pernyataan itu benar untuk suatu bilangan bulat non-negatif k, maka pernyataan tersebut juga benar untuk k+1.
Secara formal, prinsip induksi matematis ini dapat diuraikan dalam dua langkah, yakni:
1. Kasus Dasar
Buktikan dulu bahwa pernyataan tersebut benar untuk kasus dasar. Misalnya, tunjukkan bahwa pernyataan itu benar untuk n = 0 atau n = 1.
2. Langkah Induksi
Anggaplah pernyataan itu benar untuk suatu bilangan bulat non-negatif k (asumsi induksi). Kemudian, gunakan asumsi tersebut untuk membuktikan bahwa pernyataan itu juga benar untuk k + 1.
Dengan demikian, jika pernyataan tersebut terbukti benar untuk kasus dasar dan benar untuk n = k mengikuti n = k+1 (langkah induksi), maka pernyataan tersebut akan benar untuk semua bilangan bulat non-negatif yang lebih besar dari atau sama dengan nilai kasus dasar.
Langkah Induksi Matematika
Langkah ini digunakan untuk membuktikan bahwa suatu pernyataan atau properti itu benar untuk semua bilangan bulat non-negatif, berdasarkan hipotesis induksi dan langkah dasar.
1. Langkah Dasar (Base Case)
Pertama, Anda perlu membuktikan bahwa pernyataan atau properti yang ingin dibuktikan benar untuk bilangan bulat terkecil yang relevan, biasanya 0 atau 1. Ini adalah langkah awal dan penting dalam metode induksi matematika.
2. Langkah Induksi (Inductive Step)
Lakukan dua langkah berikut untuk membuktikan bahwa pernyataan atau properti juga benar untuk bilangan bulat berikutnya.
a. Hipotesis Induksi
Anda asumsikan bahwa pernyataan atau properti benar untuk suatu bilangan bulat tertentu (misalnya, k).
b. Langkah Induksi
Kemudian, Anda menggunakan hipotesis induksi untuk membuktikan bahwa pernyataan atau properti tersebut juga benar untuk bilangan bulat berikutnya (yaitu, k+1).
Dengan cara ini, Anda membuktikan bahwa jika pernyataan atau properti benar untuk kasus dasar (langkah dasar) dan benar untuk bilangan bulat k, maka pernyataan atau properti tersebut juga benar untuk bilangan bulat k+1 (langkah induksi).
Rumus ini dapat digunakan untuk membuktikan berbagai jenis pernyataan matematika, seperti rumus-rumus penjumlahan, sifat-sifat barisan, dan sifat-sifat angka, asalkan pernyataan tersebut berlaku untuk semua bilangan bulat non-negatif.
Contoh Soal
Berikut adalah contoh sederhana penerapan metode induksi matematika untuk membuktikan pernyataan matematika.
Soal 1

Pembahasan:
Langkah 1 (Langkah Dasar)

Jadi, langkah dasar terbukti benar.
Langkah 2 (Hipotesis Induksi)

Langkah 3 (Langkah Induksi)

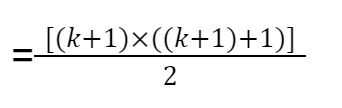
Langkah Induksi Lompatan:
Karena langkah induksi basis terbukti benar, maka pernyataan tersebut benar untuk n= k+1.
Dengan demikian, kita telah membuktikan bahwa pernyataan tersebut benar untuk setiap bilangan bulat positif n melalui metode induksi matematika.
Soal 2
Buktikan dengan menggunakan induksi matematika bahwa untuk setiap bilangan bulat positif n, 1 + 3 + 5 + … + (2n-1) = n².
Pembahasan:
Langkah 1 (Langkah Dasar)
Jika n = 1, maka 2n – 1 = 2 . 1 – 1 = 2 – 1 = 1.
Sementara n² = 1² = 1
Pernyataan ini benar untuk n = 1.
Langkah 2 (Hipotesis Induksi)
Kita asumsikan bahwa pernyataan tersebut benar untuk suatu bilangan bulat k, yaitu 1 + 3 + 5 + … + (2k-1) = k².
Langkah 3 (Langkah Induksi)
Kita akan buktikan bahwa pernyataan tersebut benar untuk n = k + 1.
Untuk n = k + 1, 1 + 3 + 5 + … + (2k-1) + (2(k+1)-1) = (k + 1)²
= k² + (2(k+1)-1)
= k² + (2k+1)
= k² + 2k + 1
= (k + 1)²
Jadi, dengan menggunakan induksi matematika, kita telah membuktikan bahwa 1 + 3 + 5 + … + (2n-1) = n² untuk setiap bilangan bulat positif n.
Soal 3
Buktikan dengan menggunakan induksi matematika bahwa untuk setiap bilangan bulat positif n, 4ⁿ – 1 habis dibagi oleh 3.
Pembahasan:
Langkah 1 (Langkah Dasar)
Jika n =1, maka 4ⁿ – 1 = 4¹ – 1 = 3
Langkah 2 (Hipotesis Induksi)
Kita asumsikan bahwa pernyataan tersebut benar untuk suatu bilangan bulat k, yaitu 4ⁿ – 1 habis dibagi oleh 3.
Langkah 3 (Langkah Induksi)
Kita akan buktikan bahwa pernyataan tersebut benar untuk n = k + 1.
Untuk n = k + 1, 4^(k+1) – 1
= 4^k . 4^1 – 1
= 4(4^k -1)
Jadi, dengan menggunakan induksi matematis tadi, kita telah membuktikan bahwa untuk setiap bilangan bulat positif n, 4ⁿ – 1 habis dibagi oleh 3.
Kesimpulan
Metode induksi matematika banyak digunakan dalam berbagai bidang matematika, seperti teori bilangan, kombinatorika, aljabar, dan analisis. Metode ini memberikan pendekatan yang kuat dan elegan untuk membuktikan pernyataan yang berlaku untuk semua bilangan bulat non-negatif.
Namun, perlu diingat bahwa induksi matematis ini hanya memberikan bukti bahwa pernyataan itu benar untuk semua nilai bilangan bulat positif, tetapi tidak menunjukkan bahwa pernyataan tersebut benar untuk nilai negatif atau pecahan.

