Dalam ilmu matematika, circle atau lingkaran adalah salah satu bentuk geometri yang paling sederhana dan paling menarik. Bagaimana tidak, bangun datar ini tidak memiliki panjang sisi dan sudut namun memiliki simetri lipat dan simetri putar yang tak terhingga.
Keindahan dan keunikan ciri fisik tersebut membuat circle mudah ditemukan di berbagai aspek kehidupan sehari-hari. Dalam artikel ini, kita akan membahas unsur-unsur utama dan rumus dasarnya dalam cakupan ilmu matematika.
Apa Itu Lingkaran?
Menurut Kamus Besar Bahasa Indonesia (KBBI), lingkaran adalah diagram yang menyatakan peristiwa dalam bentuk melingkar membentuk sudut 360 derajat. Lingkaran juga merujuk pada garis lengkung yang kedua ujungnya bertemu pada garis dan titik yang sama.
Dalam bidang geometri, bentuk yang dalam bahasa Inggris circle ini merupakan bangun datar dua dimensi yang mana memiliki sebutan tak hingga. Sebab, jumlah titik-titik yang tak terhingga ini akan membentuk suatu bulatan utuh. Titik-titik tersebut memiliki jarak yang sama terhadap pusat bangun datar ini.
Selain itu, circle juga memiliki banyak sebutan. Misalnya, berdasarkan bentuk tiga dimensinya, ia disebut sebagai bulat. Sebab, bentuk tiga dimensi memiliki isi, massa dan volume.
Terdapat dua unsur yang selalu berkaitan di materi bangun datar satu ini, yaitu jari-jari dan diameter. Jari-jari merupakan jarak titik pusat ke luar garis, sedangkan diameter merupakan jarak yang membagi lingkaran menjadi dua bagian sama besar.
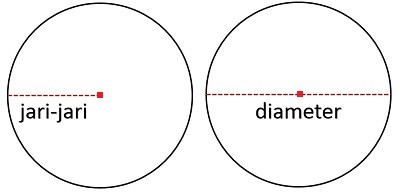
Bangun datar yang tidak memiliki sudut ini memiliki beberapa ciri-ciri, di antaranya adalah sebagai berikut:
- Jumlah sudut 180o.
- Diameter yang membaginya menjadi bidang seimbang.
- Terdapat diameter konstan yaitu garis yang menghubungkan antara titik pusat dan titik busur.
- Memiliki simetri lipat dan simetri putar tak terdefinisi.
Unsur-Unsur Bangun Datar Lingkaran
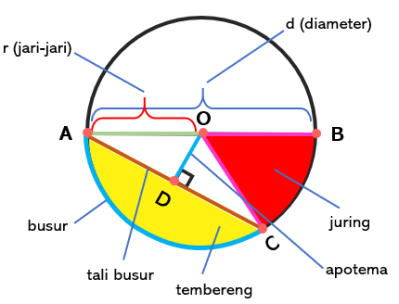
Dalam memahami bidang geometri, terdapat beberapa unsur-unsur lingkaran yang wajib Anda ketahui. Beberapa diantaranya adalah:
1. Titik Pusat
Titik pusat adalah titik dengan jarak yang sama terhadap semua titik di dalamnya. Dengan memanfaatkan alat menggambar seperti jangka, pensil, dan penggaris, Anda bisa langsung mengetahui di mana titik pusat berada. Biasanya, letak titik pusat berada tepat di tengah lingkaran dengan simbol O, P, D, Q, dan abjad lainnya.
2. Jari-jari
Seperti yang telah kita singgung sebelumnya, jari-jari merupakan suatu garis yang menghubungkan titik pusat dengan ruas garis luar. Secara matematis, simbol jari-jari adalah r kecil yang memiliki arti radius.
Ternyata, bangun datar yang tidak memiliki kurva ini memiliki kelebihan untuk memahami konsep jari-jari. Sebab, nilai jarak titik pusat ke semua titik keliling adalah sama, sehingga jarak untuk mengetahui jari-jari dapat terbentang ke atas, bawah, kanan, maupun kiri.
3. Diameter
Diameter merupakan salah satu unsur yang paling sering muncul dalam formula matematis yang memiliki simbol huruf kecil (d). Rumus diameter itu dua kali jari-jari, sehingga untuk mencari diameter, Anda hanya perlu mengalikan dua kali nilai jari-jari.
Begitu pun sebaliknya, jika mencari jari-jari, Anda hanya perlu membagi dua nilai diameter. Oleh karena itu, Anda bisa mengingat diameter sebagai panjang garis yang menghubungkan dua titik pada keliling lingkaran.
Di bagian inilah Anda bisa menemukan simetri lipat. Sebab, jika Anda melipat suatu bangun yang berbentuk bundaran, maka bangun tersebut akan membagi dua bagian yang sama besar.
4. Tali Busur
Unsur selanjutnya yang juga tidak kalah penting adalah tali busur. Tanpa tali busur, Anda tidak bisa menentukan letak tembereng dan juring. Titik busur ini merupakan garis yang melintang tanpa melewati pusat bulatan.
Dalam gambar di atas, garis AC merupakan tali busur. Sebab, garis tersebut terhubung antara titik C ke titik A pada keliling bangun datar yang berbentuk bulat.
5. Busur
Berbeda dengan tali busur, busur merupakan garis melengkung pada kelilingnya yang menghubungkan titik pada tali busur. Seperti pada gambar di atas, busur terletak pada sudut A-C, B-A, dan C-B.
Unsur busur ini memiliki tiga jenis, yaitu busur kecil, busur besar, dan busur setengah lingkaran. Ketiganya dapat Anda pahami melalui bentuk busur itu sendiri. Tolok ukurnya adalah berdasarkan pada ukuran setengah bundaran atau setara dengan 180 derajat.
Jika ukurannya melebihi 180 derajat, maka Anda bisa menggolongkannya ke dalam busur besar,kemudian jika lebih kecil, maka termasuk busur kecil. Sedangkan, busur setengah lingkaran adalah busur dengan ukuran yang sama dengan 180 derajat.
6. Tembereng
Berikutnya adalah tembereng yang merupakan bagian dalam bulatan dan diapit oleh busur dan tali busur. Berdasarkan bentuknya, tembereng juga terbagi menjadi dua, yaitu tembereng besar dan kecil.
7. Juring
Berbeda dengan tembereng, juring merupakan daerah yang diapit oleh dua jari-jari dan busur. Berdasarkan ukurannya, Anda juga bisa membagi menjadi tiga bagian, yaitu juring besar, kecil, dan setengah lingkaran.
8. Apotema
Unsur yang terakhir adalah apotema. Apotema merupakan garis yang menghubungkan antara titik pusat dengan titik pada tali busur. Jika Anda menghubungkan garis tersebut, maka Anda akan menemukan dua garis yang saling berpotongan membentuk siku-siku.
Rumus-Rumus dan Contoh Soal Lingkaran
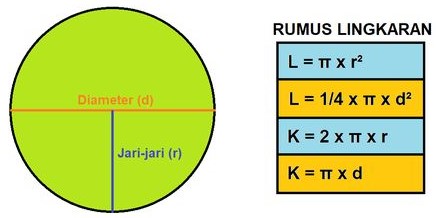
Pada umumnya, rumus bangun datar mirip ellips ini terbagi atas keliling dan luas. Keduanya sangat mudah untuk Anda pahami. Berikut ini rumus-rumusnya:
1. Keliling
Keliling merupakan bagian busur terpanjang pada bangun datar yang berbentuk bulat ini. Cara perhitungannya pun cukup mudah, namun terdapat dua jenis rumus yang biasa digunakan, yaitu jika diketahui diameter atau jari-jari.
Berikut formula rumusnya:
- Jika menggunakan diameter:
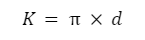
- Jika menggunakan jari-jari:
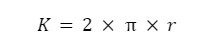
Contoh soal:
1. Jika sebuah lingkaran memiliki jari-jari 3 cm, maka berapakah panjang tali busur terpanjangnya?
Jawab:
- Tali busur terpanjang adalah diameter, maka:
d = 2 x r
d = 2 x 3= 6 cm
2. Sebuah jam berbentuk bulat dengan jarum menit memiliki panjang 21 cm. Berapakah jarak yang ditempuh ujung tersebut selama 1 jam?
Jawab:
- Jarak tempuh satu jam merupakan bagian dari keliling lingkaran, sehingga jawabannya adalah:
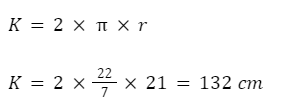
2. Luas
Luas merupakan daerah yang dibatasi oleh keliling. Rumus luas ini berhubungan jari-jari, sehingga harus terdapat data nilai jari-jari pada lingkaran. Berikut formulanya:
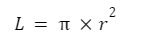
Anda bisa berlatih dengan contoh soal berikut ini:
1. Sebuah meja berbentuk lingkaran memiliki diameter 100 cm. Ayah akan memberikan kaca pada bagian atas meja sesuai dengan luasnya meja tersebut. Berapakah luas kaca diperlukan?
Pembahasan:
- Dari soal di atas, diketahui nilai diameter, maka rumus luasnya adalah sebagai berikut:
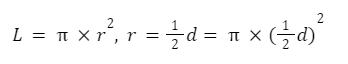
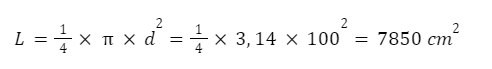
2. Pemerintah kota memiliki rencana untuk membangun sebuah taman dengan diameter 56 m beserta kolam ikan di dalamnya dengan diameter 28 m. Jika pemerintah ingin menanam rumput di luar kolam dengan biaya Rp6.000,00/m2, maka berapa total biaya yang dikeluarkan oleh pemerintah?
Jawab:
- Untuk mencari luas untuk menanam rumput, maka dapat dilakukan dengan cara mengurangi luas sebuah taman dengan luas kolam. Berikut perhitungannya:

Baca Juga : Rumus Bola (Luas, Keliling, Volume), Contoh, dan Pembahasan
Temukan Contoh Lingkaran di Sekitar Anda!
Sebenarnya, banyak sekali barang-barang di sekitar Anda yang memiliki bentuk lingkaran. Contohnya adalah ban sepeda, jam dinding, piring, mangkok, wadah kosmetik, dan uang koin. Meskipun ia berbentuk bulat tanpa memiliki sisi, lingkaran memiliki bentuk yang cukup unik untuk pembuatan kerajinan kayu seperti meja, jendela, dan asbak. Oleh karena itu, kerajinan-kerajinan yang memanfaatkan bentuk cetakan bulat ini memiliki nilai yang lebih estetis.

