Pernahkah kalian mendengar teori peluang? Konsep teori peluang dalam matematika digunakan untuk memprediksi kemungkinan pada suatu peristiwa yang sedang berlangsung. Dalam teori peluang, salah satunya adalah peluang kejadian majemuk yang dapat memprediksi dua bahkan lebih kemungkinan yang akan terjadi.
Lalu, bagaimana cara mengerjakan peluang kejadian majemuk dalam soal matematika? Yuk, simak penjelasannya berikut ini!
Pengertian Peluang Kejadian Majemuk
Sesuai namanya, peluang kejadian majemuk digunakan sebagai cara untuk memprediksi tidak hanya satu kejadian saja, namun bisa dua atau lebih secara bersamaan. Jadi, kamu bisa mengetahui seberapa besar kemungkinan tersebut bisa terjadi.
Misalnya, dalam suatu kotak mainan terdapat banyak bola warna-warni. Kemudian, kamu mengambil bola tersebut secara acak. Maka, konsep peluang dapat digunakan untuk mengetahui kira-kira peluang warna apa saja yang dapat terambil.
Kejadian majemuk mencakup dua hal utama, yaitu:
- Irisan dua kejadian yang memiliki tanda “೧” dan identik dengan kata “dan”.
- Gabungan dua kejadian yang memiliki tanda “∪” dan identik dengan kata “atau”.
Jenis Peluang Kejadian Majemuk

Peluang kejadian majemuk ini memiliki 4 jenis, yaitu kejadian yang saling lepas, kejadian yang saling tidak lepas, kejadian yang saling bebas, dan kejadian yang saling tidak bebas. Apa perbedaan di antara keempat jenis peluang ini? Yuk, cari tahu!
1. Kejadian Majemuk Saling Lepas
Jenis yang pertama yaitu kejadian majemuk saling lepas. Sederhananya, terdapat dua kejadian A dan B namun tidak saling terkait atau tidak ada persekutuan. Jadi, pada intinya, kejadian majemuk saling lepas tidak memiliki irisan.
Perhatikan diagaram venn di bawah ini!
(Diagram Venn Kejadian Majemuk Saling Lepas | Sumber gambar: pijarbelajar.id)
Dari diagram venn di atas, terlihat jelas bahwa A dan B pada semesta (S) dikatakan saling lepas atau tidak terkait satu sama lain. Maka, keduanya tidak memiliki irisan atau sama dengan nol. Dalam hal ini dituliskan dengan n(A೧B)=0.
Keterangan:
Semesta (S) = {1,2, 3, 4, 5, 6}
Bilangan ganjil (A) = {1, 3, 5}
Bilangan genap (B) = {2, 4, 6}
Banyaknya kejadian masing-masing dapat dituliskan menggunakan simbol seperti di bawah ini:
n(S) = 6
n(A) = 3
n(B) = 3
Jadi, rumus yang digunakan untuk menghitung peluang kejadian majemuk saling lepas dari setiap kejadian A dan B yaitu:
P(A∪B) = P(A) + P(B)
Sehingga, untuk menghitung nilai peluang A dan peluang B dengan rumus tersebut menjadi:
P(A∪B) = P(A) + P(B)
P(A∪B) = ½ + ½
P(A∪B) = 1
Maka, bisa dikatakan peluang gabungan A dan B adalah 1.
2. Kejadian Majemuk Tidak Saling Lepas
Jika terdapat elemen pada kejadian A dan B yang beririsan, maka disebut dengan kejadian majemuk tidak saling lepas. Kejadian ini memang kebalikan dari kejadian majemuk saling lepas yang tidak memiliki irisan sama sekali. Maka, irisan A dan B pada kejadian majemuk tidak saling lepas tidak sama dengan 0 atau n(A೧B) ≠ 0.
Adapun rumus untuk peluang kejadian majemuk saling tidak lepas yaitu:
P(A∪B) = P(A) + P(B) – P(A೧B)
3. Kejadian Majemuk Saling Bebas
Selanjutnya, peluang kejadian majemuk saling bebas adalah peluang di mana peluang terjadinya suatu kejadian (A) yang tidak terpengaruh dengan kejadian lainnya (B). Begitupun juga sebaliknya. Dengan kata lain, dua kejadian tersebut berlangsung secara independen.
Rumus untuk peluang kejadian majemuk saling lepas yaitu:
P(A೧B) = P(A) x P(B)
4. Kejadian Majemuk Tidak Saling Bebas
Jenis peluang yang terakhir yaitu kejadian majemuk tidak saling bebas atau juga disebut sebagai peluang kejadian majemuk bersyarat. Sederhananya, tidak saling bebas terjadi jika ada dua kejadian yang berbeda yang kemungkinan kejadiannya ditentukan dengan kejadian lainnya.
Rumus untuk menentukan peluang tidak saling bebas yaitu:
P(A೧B) = P(A) x P(B\A)
Contoh Soal & Pembahasan
Berikut adalah latihan soal untuk mengasah tingkat pemahaman mengenai peluang kejadian majemuk.
Soal 1
Tentukan peluang munculnya mata dadu ganji atau prima dalam pelemparan sebuah mata dadu!
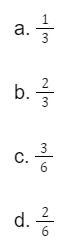
Jawaban: b.
Pembahasan: Kejadian A adalah munculnya mata dadu ganjil dan kejadian B yaitu munculnya mata dadu prima.

Dalam soal ini, terdapat 2 anggota yang beririsan, sehingga dapat menggunakan rumus peluang kejadian majemuk tidak saling lepas dengan rumus sebagai berikut:

Maka, jawaban yang benar adalah ⅔.
Soal 2
Di dalam sebuah kotak terdapat 2 bola kuning dan 3 bola biru. Beni mengambil dua bola satu per satu tanpa pengembalian. Jika pada pengambilan pertama Beni mendapatkan bola biru dengan peluang pengambilan 3/5, maka berapakah peluang terambilnya bola berwarna kuning pada pengambilan kedua?
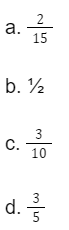
Jawaban: c.
Pembahasan:
Dalam soal ini, kamu dapat menggunakan rumus peluang kejadian majemuk tidak saling bebas dengan menggunakan rumus P(A೧B) = P(A) x P(B|A).
P(A)= 3/5, yang perlu dicari terlebih dahulu adalah P(B|A) untuk mengetahui P(A೧B).

P(A೧B) = P(A) x P(B|A)

Soal 3
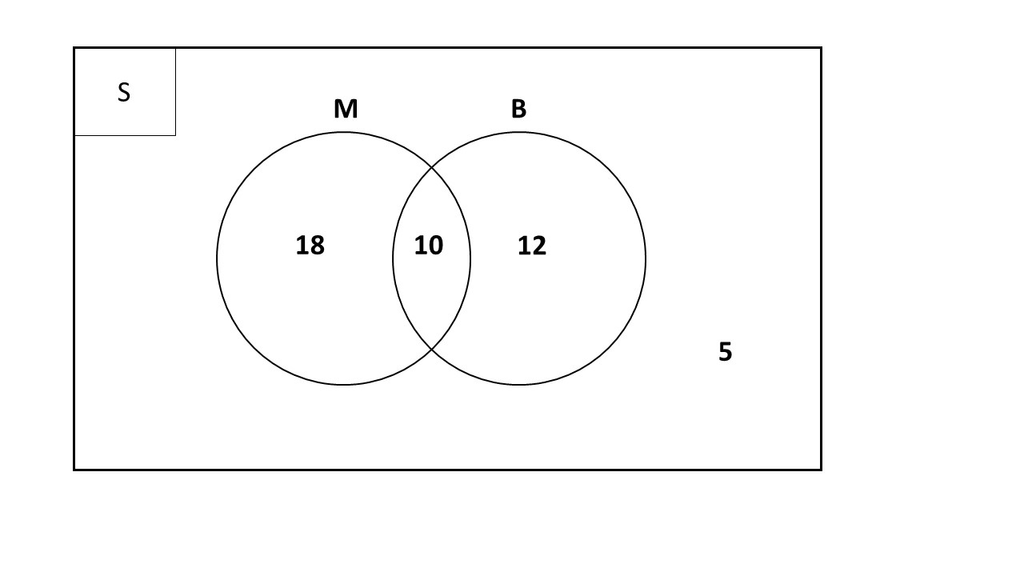
Di suatu kelas terdapat 45 siswa. Dari jumlah siswa tersebut, 28 siswa suka bahasa Inggris, 22 siswa suka Matematika, dan 10 siswa suka kedua-duanya. Jika seorang siswa terpilih secara acak, tentukan peluang siswa yang terpilih adalah yang menyukai Matematika atau bahasa Inggris!

Jawaban: a.
Pembahasan:
- n(S) = 45
- n(A), siswa suka Matematika = 28
- n(B), siswa suka Bahasa Inggris = 22
- n(A೧B), suka keduanya = 10
Sehingga, peluang terpilih yang suka Matematika atau Bahasa Inggris adalah:
P(A∪B) = P(A) + P(B) – P(A೧B)

Soal 4
Selin melempar dua buah mata dadu yang memiliki nilai semesta 36. Hitung peluang munculnya mata dadu yang berjumlah 2 atau 4!

Jawaban: d.
Pembahasan:
- n(S) = 36
- n(A) = 1
- n(B) = 3
Soal ini mengunakan rumus peluang kejadian saling lepas, maka:
P(A∪B) = P(A) + P(B)
P(A) = n(A)/n(S) = 136
P(B) = n(B)/n(S) = 336
Sehingga
P(A∪B) = P(A) + P(B)
= 136 + 336
= 436 = 19
Maka, peluang munculnya mata dadu yang berjumlah 2 atau 4 yaitu 19.
Jadi, Sudah Paham dengan Peluang Kejadian Majemuk?
Itu tadi penjelasan mengenai peluang kejadian majemuk yang bisa kamu pelajari beserta latihan soalnya. Semoga artikel ini membantumu untuk memahami materi peluang. Terus berlatih dengan mengerjalan latihan soal supaya makin paham.

