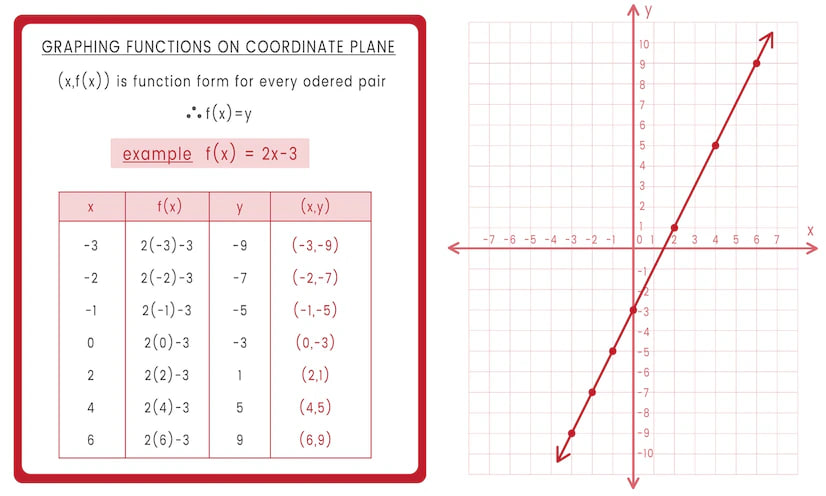
Persamaan garis lurus adalah salah satu konsep dasar matematika yang berperan penting dalam geometri analitik. Dengan pemahaman tentang persamaan ini, Anda dapat menggambarkan dan memahami hubungan antara dua variabel dalam bentuk garis-garis lurus.
Artikel ini akan menjelaskan pengertian persamaan garis lurus, sifat-sifatnya, rumus yang bergunakan untuk menyusunnya, dan memberikan contoh soal untuk memperkuat pemahaman Anda. Baca artikel ini sampai selesai, ya!
Apa yang Dimaksud dengan Persamaan Garis Lurus?
Persamaan garis lurus adalah cara matematis untuk menggambarkan hubungan antara dua variabel, biasanya berupa x dan y yang berpangkat satu. Persamaan ini memberitahu kita tentang garis yang menghubungkan semua titik pada grafik.
Jika persamaan tersebut digambarkan dalam koordinat Cartesius, maka akan menghasilkan grafik berbentuk garis lurus dengan sudut kemiringan khusus. Sudut kemiringan ini sering disebut sebagai nilai gradien garis (m).
Persamaan ini juga memberikan informasi penting seperti seberapa curam garisnya (kemiringan). Secara khusus garis yang memotong sumbu x dan sumbu y, sehingga bermanfaat untuk mengenali titik-titik di grafik.
Biasanya, Anda dapat menentukan persamaan garis lurus dengan berbagai cara. Mulai dari menggunakan bentuk titik-kemiringan, bentuk intersepsi-lereng, bentuk dua titik, atau bentuk standar.
Persamaan Umum Garis
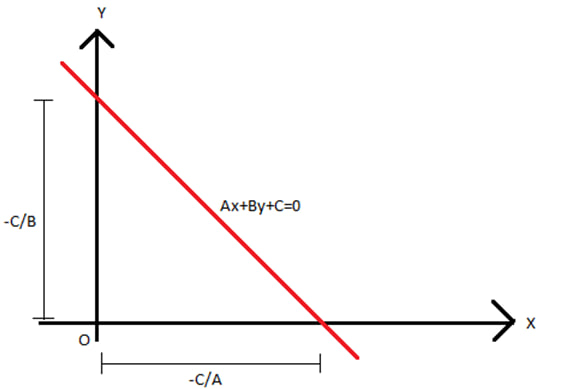
Persamaan umum garis dalam dua variabel tingkat pertama representasinya sebagai berikut:
Ax + By + C = 0,
A, B ≠ 0 di mana A, B dan C adalah konstanta yang termasuk bilangan real. Ketika Anda mewakili persamaan secara geometris, maka Anda akan selalu mendapatkan garis-garis lurus.
Bentuk dan Rumus Persamaan Garis Lurus
Bentuk-bentuk ini membantu Anda memahami bagaimana menemukan persamaan garis lurus dengan informasi yang telah ada. Berikut ini adalah representasi rumus garis lurus dalam berbagai bentuk:
1. Bentuk Standar
Persamaan garis dalam bentuk standar dituliskan sebagai:
Ax + By = C
Dalam persamaan tersebut, A, B, dan C adalah sebagai konstanta bilangan bulat. Anda harus ingat bahwa baik A maupun B harus memiliki nilai yang tidak nol secara bersamaan.
2. Persamaan Bentuk Titik-Kemiringan
Persamaan bentuk titik-kemiringan berguna untuk menemukan persamaan garis lurus yang melewati suatu titik tertentu dengan koordinat (x1, y1) dan memiliki kemiringan (slope) m. Dengan rumus y – y1 = m (x – x1), di mana (x, y) adalah titik apa pun di dalam grafik garis tersebut.
3. Persamaan Bentuk Slope-Intercept
Persamaan bentuk intersep lereng garis lurus menyatakan bahwa jika Anda tahu kemiringan garis (m) dan titik di mana garis tersebut memotong sumbu y (b). Maka, Anda bisa mengekspresikan garis tersebut dengan cara yang sangat sederhana. Ini berarti bahwa garis lurus akan selalu melalui titik (0, b) pada grafik.
Jadi, dengan menggunakan rumus titik-kemiringan, Anda dapat menyusun persamaan garis ini menjadi sesuatu yang lebih mudah dimengerti sebagai berikut:
y – b = m(x – 0)
y = mx + b
Dalam rumus tersebut, y adalah nilai pada sumbu y dan m adalah kemiringan garis. Kemudian, x adalah nilai pada sumbu x dan b adalah titik potong garis dengan sumbu y.
4. Persamaan Bentuk Dua Titik
Anda juga dapat menemukan persamaan garis lurus saat Anda memiliki dua titik, A (x1, y1) dan B (x2, y2), yang mana menjadi titik-titik pada garis tersebut. Anda juga akan mempertimbangkan titik P (x, y), yang bisa berada di mana saja pada garis itu.
Mulailah dengan menghitung kemiringan garis AB menggunakan rumus: (y1 – y2) / (x1 – x2). Sekarang, Anda perlu mengetahui kemiringan garis AP di mana diketahui titik A, B, dan P berada dalam satu garis lurus.
Kemiringan garis AB = y1 – y2 / x1 – x2
Kemiringan garis AP = y1 – y2 / x1 – x2
Jadi, Anda menggunakan prinsip ini untuk menghitung kemiringan garis AP dengan rumus yang sama, yaitu (y – y1) / (x – x1). Ketika Anda mengeksplorasi hubungan ini lebih lanjut, Anda akan melihat bahwa kedua rumus memiliki bentuk yang sama, yaitu (y1 – y2) / (x1 – x2).
Garis AB = y – y1 / x – x1 = y1 – y2 / x1 – x2
Menjadi (y – y1) = y2 – y1 / x2 – x1 (x – x1)
Oleh karena itu, satu persamaan garis lurus ini berlaku untuk setiap koordinat titik yang berada pada garis AB. Inilah mengapa Anda dapat menggunakannya sebagai persamaan umum untuk garis-garis lurus AB.
5. Persamaan Bentuk Intersep
Ketika sebuah garis memotong sumbu x di titik (a, 0) dan sumbu y di titik (0, b), Anda dapat menyebutnya sebagai titik potong x dan titik potong y. Persamaan yang menggambarkan garis lurus dengan titik potong x a dan titik potong y b adalah (x/a) + (y/b) = 1.
Jika Anda memiliki persamaan garis dalam bentuk umumnya, yaitu ax + by = c, dan nilai c tidak sama dengan 0. Maka Anda dapat menghitung titik potong x sebagai -c/a dan titik potong y sebagai -c/b.
Rumus Persamaan Garis Lurus
Berikut adalah berbagai rumus dan bentuk persamaan garis lurus:
1. Persamaan Umum
Rumus persamaan garis lurus dalam bentuk umumnya adalah:
Ax + By + C = 0
2. Persamaan Standar
Sedangkan rumus persamaan garis yang terstandar adalah:
Ax + By = C
Dalam persamaan tersebut, A, B, dan C adalah konstanta bilangan bulat. Kemudian, A dan B tidak boleh nol secara bersamaan.
3. Persamaan Garis Horizontal
Rumus persamaan garis horizontal adalah:
y = a, (a ∈ R)
Dalam persamaan tersebut, a adalah konstanta, dan garis ini sejajar dengan sumbu x.
4. Persamaan Garis Vertikal
Rumus persamaan garis vertikal adalah:
x = b, (b ∈ R)
Dalam persamaan tersebut, b adalah konstanta, dan garis ini sejajar dengan sumbu y.
5. Bentuk Dua Titik
Jika garis melewati dua titik (x1, y1) dan (x2, y2), maka kemiringannya (m) dan persamaannya adalah m = (y2 – y1) / (x2 – x1). Kemudian, Anda dapat menggunakan formula titik-kemiringan y – y1 = m(x – x1).
6. Slope-intercept
Jika Anda tahu kemiringan (m) dan titik potong y (c), maka persamaannya adalah:
y = mx + c
7. Intercept
Rumus persamaan garis intersep adalah:
(x / a) + (y / b) = 1
Ini adalah beberapa bentuk dasar persamaan garis lurus yang digunakan dalam matematika. Anda dapat memilih bentuk yang sesuai dengan informasi yang Anda miliki atau situasi yang Anda hadapi untuk menemukan persamaan garis yang Anda butuhkan.
Persamaan Garis Lurus pada Grafik
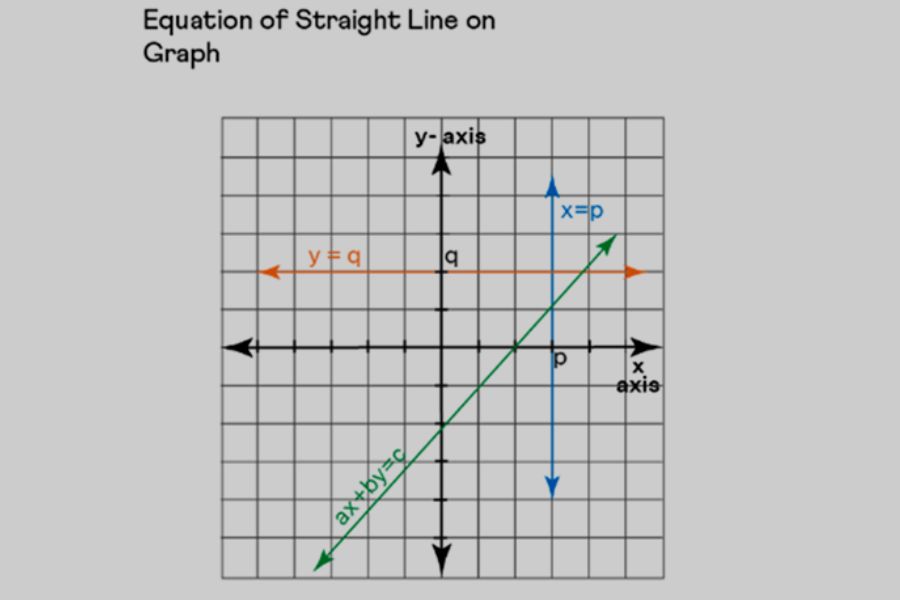
Dalam grafik, ketika Anda memiliki persamaan linear dengan satu variabel (misalnya, x), garis yang dihasilkan akan berbentuk vertikal dan sejajar dengan sumbu y. Sebaliknya, jika Anda memiliki persamaan dengan satu variabel (misalnya, y), garis yang terbentuk akan horizontal dan sejajar dengan sumbu x.
Namun, ketika Anda memiliki persamaan linear dengan dua variabel (x dan y), grafiknya akan berupa garis lurus yang memiliki kemiringan tertentu. Kemiringan positif menunjukkan garis yang naik dari kiri ke kanan, sementara kemiringan negatif mengindikasikan garis yang turun.
Contoh Soal Persamaan Garis Lurus
Supaya pemahaman Anda terkait persamaan garis semakin mendalam, perhatikan dan pelajari contoh soal di bawah ini:
1. Contoh Soal 1
Temukan kemiringan dan titik potong y dari garis dengan persamaan 3x – 5y + 6 = 0.
Pembahasan:
Untuk menemukan kemiringan (slope) dan titik potong y dari garis dengan persamaan 3x – 5y + 6 = 0, Anda perlu mengubahnya ke dalam bentuk yang lebih sederhana. Berikut langkah-langkahnya:
- Mulai dengan persamaan awal: 3x – 5y + 6 = 0.
- Kemudian, pindahkan 3x ke sisi sebelah kanan dengan mengurangkan 3x dari kedua sisi persamaan: -5y = -3x – 6.
- Sekarang, bagi kedua sisi persamaan dengan -5 untuk mengisolasi y: y = (3x + 6)/5.
Dengan begitu, Anda telah mengubah persamaan garis lurus ke dalam bentuk slope-intercept (y = mx + c):
- Kemiringan (slope), yang disimbolkan dengan m, adalah 3/5.
- Titik potong y (y-intercept), yang disimbolkan dengan c, adalah 6/5.
Jadi, garis tersebut memiliki kemiringan 3/5 dan memotong sumbu y pada 6/5.
2. Contoh Soal 2
Gambar grafik persamaan linear 3x + 4y = 6. Pada titik mana grafik memotong sumbu x dan sumbu y?
Pembahasan:
Mari kita gambar grafik dari persamaan linear 3x + 4y = 6 dan temukan di mana grafik ini memotong sumbu x dan sumbu y. Langkah-langkahnya adalah sebagai berikut:
1. Titik Potong Sumbu X
Untuk menemukan di mana grafik memotong sumbu x, Anda atur y menjadi 0 dalam persamaan. Sehingga, hasil hitungannya adalah:
3x + 4(0) = 6
3x = 6
x = 2
Jadi, titik di mana grafik memotong sumbu x adalah (2, 0).
2. Titik Potong Sumbu Y
Kemudian, untuk menemukan di mana grafik memotong sumbu y, Anda atur x menjadi 0 dalam persamaan. Sehingga, hasil hitungannya adalah:
3(0) + 4y = 6
4y = 6
y = 6/4
y = 1,5
Jadi, titik di mana grafik memotong sumbu y adalah (0, 1,5).
Sekarang, Anda dapat memplot titik-titik ini pada grafik untuk mendapatkan gambaran visual tentang persamaan tersebut.

Sudah Paham dengan Teori Persamaan Garis Lurus?
Tentu, sekarang Anda telah memahami konsep dasar persamaan garis lurus. Mulai dari bentuk umum hingga bentuk slope-intercept, Anda telah mempelajari cara menggambarkan dan menganalisis garis dalam berbagai situasi. Anda juga telah melihat bagaimana mencari kemiringan, titik potong x, dan titik potong y.
Persamaan garis lurus adalah dasar yang penting dalam matematika dan memiliki berbagai aplikasi dalam ilmu pengetahuan dan kehidupan sehari-hari. Misalnya dalam fisika, persamaan ini berguna untuk menggambarkan gerak lurus, hukum Hooke tentang elastisitas, dan hukum termodinamika dasar.
Kemudian, dalam teknik, persamaan garis berguna dalam berbagai konteks, termasuk dalam perancangan struktur bangunan, jembatan, dan perencanaan rute untuk perjalanan transportasi. Maka dari itu, teruslah berlatih dan eksplorasi lebih lanjut untuk memperkuat pemahaman Anda tentang konsep ini.