Rumus GGL Induksi Beserta Faktor, Penerapan, dan Contoh Soalnya

Mengetahui rumus GGL (Gaya Gerak Listrik) induksi sangatlah penting dalam dunia fisika karena rumus tersebut memiliki peran yang besar dalam berbagai aplikasi teknologi. Mengingat bahwa GGL induksi adalah gaya yang timbul akibat perubahan fluks magnetik pada kawat atau kumparan. 

Dalam artikel ini, kita akan mengupas secara mendalam tentang konsep GGL induksi, faktor-faktor yang mempengaruhinya, berbagai rumus yang terkait, serta penerapannya dalam kehidupan sehari-hari. Selain itu, kami juga akan menyajikan contoh soal dan pembahasannya untuk memperkuat pemahaman Anda.

Konsep GGL Induksi dan Hubungannya dengan Fluks Magnetik 

Sebelum langsung mempelajari rumus GGL induksi, Anda perlu memahami konsep GGL induksi itu sendiri. 

Singkatnya, GGL induksi muncul sebagai akibat dari perubahan fluks magnetik melalui suatu kawat atau kumparan. Sementara fluks magnetik (Φ) adalah besaran yang mengukur jumlah medan magnet yang melintasi area tertentu. 

Ketika fluks magnetik berubah dengan cepat, maka GGL induksi akan timbul pada kawat atau kumparan sebagai efek induksi elektromagnetik. Efek ini merupakan salah satu dasar penting dalam induksi elektromagnetik, khususnya untuk berbagai aplikasi teknologi modern seperti generator listrik, transformator, dan lain-lain. 

Perubahan fluks magnetik dapat terjadi karena berbagai faktor, seperti perubahan kuat medan magnet yang melintasi kawat atau pergerakan magnet terhadap kawat tersebut.

Faktor-Faktor yang Mempengaruhi Besarnya GGL Induksi

Besarnya GGL induksi dipengaruhi oleh beberapa faktor, antara lain:

• Jumlah lilitan: Semakin banyak jumlah lilitan pada kawat atau kumparan, semakin besar pula hasil GGL induksi.
• Kuat medan magnet: Semakin besar kuat medan magnet yang melintasi kawat, semakin besar pula GGL induksi yang timbul.
• Luas bidang kumparan: Semakin besar luas bidang kumparan, semakin besar pula hasil GGL induksi.
• Kecepatan gerak magnet: Perubahan fluks magnetik yang lebih cepat akan menghasilkan GGL induksi yang lebih besar pada kawat.
• Bahan lilitan: Jenis bahan kawat atau kumparan juga dapat mempengaruhi besarnya GGL induksi yang dihasilkan.

Macam-macam Persamaan dan Rumus GGL Induksi

Dalam kaitannya dengan faktor-faktor yang mempengaruhi GGL induksi, terdapat beberapa rumus dan persamaan yang perlu Anda pahami dengan baik. Berikut ini adalah berbagai formula dan persamaan yang terkait dengan GGL induksi:

1. Hukum Faraday

Hukum Faraday menyatakan bahwa besarnya GGL induksi pada suatu kawat akan berbanding lurus dengan laju perubahan pada fluks magnetik yang melintasi kawat tersebut. Rumus GGL induksi pada hukum ini adalah:

ε = -N * ΔΦ / Δt

Dalam rumus tersebut, ε adalah GGL induksi (V atau volt). Kemudian, N adalah jumlah lilitan pada kawat, ΔΦ adalah perubahan fluks magnetik (Wb atau weber), dan Δt adalah perubahan waktu (s atau detik).

2. Rumus GGL Induksi pada Kumparan

Sedangkan untuk kumparan, rumus GGL induksi dapat dituliskan sebagai berikut:

ε = -N * dΦ / dt

Dalam rumus tersebut, ε adalah GGL induksi (V atau volt). Lalu N adalah jumlah lilitan pada kumparan, dan dΦ/dt adalah turunan fluks magnetik terhadap waktu (Wb/s atau weber per detik).

3. Hukum Lenz

Hukum Lenz menyatakan bahwa arah GGL induksi akan selalu berlawanan dengan perubahan fluks magnetik yang menyebabkannya. Dalam hukum ini, GGL induksi cenderung menghasilkan arus yang menghasilkan medan magnet yang berlawanan dengan perubahan medan magnet yang menyebabkan induksi tersebut.

Adapun persamaan matematikanya adalah:

Arah arus listrik = − dΦ/dt​

Formula dΦ/dt adalah laju perubahan fluks magnetik yang melintasi kawat atau konduktor, dan satuannya yaitu weber per detik, Wb/s. Jadi, Hukum Lenz sangat penting dalam menghindari terjadinya arus berlawanan penyebab kerusakan perangkat atau sistem yang menggunakan induksi elektromagnetik.

4. Rumus GGL Induksi pada Kumparan yang Berputar

Ketika kumparan berputar dalam medan magnet yang konstan, rumus GGL induksi yang dapat berguna untuk menghitungnya yaitu:

ε = N x B x A x ω x sin(θ)

Keterangan: 

• ε = GGL induksi (V atau volt) 
• N = jumlah lilitan pada kumparan 
• B = kuat medan magnet (T atau tesla) 
• A = luas penampang melintang kumparan (m²) 
• ω = kecepatan sudut kumparan (rad/s) 
• θ = sudut antara garis normal kumparan dengan garis medan magnet (derajat)

5. Rumus GGL Induksi pada Kumparan yang Bergerak

Ketika kumparan dengan panjang L bergerak dengan kecepatan v dalam medan magnet B yang konstan, maka perhitungan rumus GGL induksinya yaitu:

ε = B * L * v

Keterangan: 

• ε = GGL induksi (V atau volt) 
• B = kuat medan magnet (T atau tesla) 
• L = panjang kumparan (m) 
• v = kecepatan kumparan (m/s)

6. Rumus GGL Induksi pada Kumparan yang Berubah Ukuran

Ketika kumparan dengan luas penampang melintang A dan jumlah lilitan N berubah ukuran dengan laju perubahan A, rumus GGL induksinya yaitu:

ε = -N x A x d(B) : dt

Keterangan: 

• ε = GGL induksi (V atau volt) 
• N = jumlah lilitan pada kumparan 
• A = luas penampang melintang kumparan (m²) 
• d(B)/dt = turunan medan magnet terhadap waktu (T/s atau tesla per detik)

Penerapan Rumus GGL Induksi

Persamaan dan rumus GGL induksi memiliki banyak penerapan praktis dalam dunia teknologi dan industri. Sebab, penerapan rumus dan persamaan ini menjadi dasar bagi berbagai perangkat elektronik dan sistem yang menggunakan prinsip induksi elektromagnetik. Beberapa contoh penerapannya adalah:

• Menghitung GGL induksi pada kumparan generator listrik untuk menghasilkan listrik dari energi kinetik.
• Menghitung GGL induksi pada kumparan transformator untuk mengubah tegangan AC dari satu tingkat ke tingkat lain.
• Penghitungan rumus GGL induksi pada kumparan pada teknologi nirkabel untuk mentransfer energi dari pengisi daya ke perangkat yang diisi dayanya.
• Menghitung GGL induksi pada kumparan sensor arus untuk mendeteksi arus listrik yang melintasi suatu kawat.
• Menghitung GGL induksi pada kumparan pada kompor listrik induksi untuk menghasilkan panas dengan cepat pada wajan atau panci.

Penerapan Konsep GGL Induksi

Konsep GGL induksi memiliki banyak penerapan praktis dalam dunia teknologi dan industri. Beberapa diantaranya adalah:

1. Generator Listrik

Generator listrik bekerja berdasarkan prinsip GGL induksi. Sebab, mereka mengubah energi kinetik menjadi energi listrik dengan memanfaatkan perubahan fluks magnetik pada kumparan.

2. Transformator

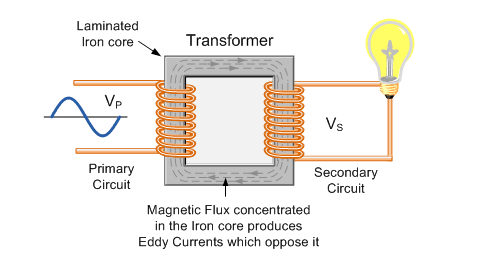
Sementara transformator adalah alat yang memanfaatkan GGL induksi untuk mengubah tegangan AC dari satu tingkat ke tingkat lain. Baik menaikkan (step-up) maupun menurunkan (step-down) tegangan.

3. Sensor Arus

Selain itu, pada beberapa perangkat elektronik, GGL induksi juga berguna sebagai sensor. Tujuannya adalah untuk mendeteksi arus listrik yang melintasi suatu kawat.

4. Teknologi Nirkabel

Teknologi nirkabel seperti pengisian daya nirkabel pada smartphone juga menggunakan prinsip GGL induksi. Kegunaannya adalah untuk mentransfer energi dari pengisi daya ke perangkat yang diisi dayanya.

Penerapan GGL Induksi dalam Kehidupan Sehari-hari

Selain dalam dunia teknologi dan industri, GGL induksi juga memiliki penerapan dalam kehidupan sehari-hari. Beberapa contoh penerapannya adalah:

• Pada kompor listrik induksi, GGL induksi berguna untuk menghasilkan panas dengan cepat pada wajan atau panci yang terbuat dari material ferromagnetik.
• Pada beberapa kendaraan modern, sensor kecepatan menggunakan prinsip GGL induksi untuk mendeteksi putaran roda dan mengukur kecepatan kendaraan.
• Sistem pengaman pintu otomatis juga menggunakan sensor GGL induksi untuk mendeteksi pergerakan objek dan menghindari benturan.
• Pada mesin penutup botol otomatis, GGL induksi berguna untuk memanaskan bagian tutup botol sehingga menutup rapat.

Contoh Soal Rumus GGL Induksi  dan Pembahasan

Simak 3 contoh soal di bawah ini untuk mempelajari lebih dalam mengenai beberapa rumus GGL induksi:

1. Contoh Soal 1

Sebuah kawat dengan panjang 2 meter dan memiliki 500 lilitan dihubungkan ke sebuah generator listrik yang menghasilkan fluks magnetik sebesar 0,03 weber. Jika fluks magnetik berubah dalam waktu 0,5 detik, hitunglah besar GGL induksi pada kawat tersebut.

Pembahasan:

Diketahui: 

N (jumlah lilitan) = 500 

ΔΦ (perubahan fluks magnetik) = 0,03 Wb 

Δt (perubahan waktu) = 0,5 detik

Jadi, rumus GGL Induksi (ε) yang dapat Anda gunakan yaitu rumus Hukum Faraday: 

ε = -N * ΔΦ / Δt 

ε = -500 * 0,03 Wb / 0,5 detik = -30 volt

Jadi, besar GGL induksi pada kawat tersebut adalah 30 volt.

2. Contoh Soal 2

Sebuah transformator memiliki 100 lilitan pada kumparannya dan menghasilkan fluks magnetik sebesar 0,02 weber. Jika transformator tersebut mampu mengubah tegangan AC dari 120 volt menjadi 240 volt, hitunglah jumlah lilitan pada kumparan kedua (secondary) transformator tersebut.

Pembahasan:

Diketahui: 

N1 (jumlah lilitan pada kumparan pertama) = 100 

Φ (fluks magnetik) = 0,02 Wb 

V1 (tegangan pada kumparan pertama) = 120 volt 

V2 (tegangan pada kumparan kedua) = 240 volt

Maka, Anda dapat menggunakan rumus transformator untuk mencari N2 (jumlah lilitan pada kumparan kedua): 

V2 / V1 = N2 / N1 

240 volt / 120 volt = N2 / 100  

2 = N2 / 100 

N2 = 2 * 100 = 200 lilitan

Jadi, jumlah lilitan pada kumparan kedua transformator tersebut adalah 200 lilitan.

3. Contoh Soal 3

Sebuah kumparan dengan 100 lilitan memiliki luas penampang melintang 0,005 m². Jika fluks magnetik yang melintasi kumparan berubah sebesar 0,02 weber dalam waktu 0,1 detik, hitunglah besar GGL induksi pada kumparan tersebut.

Pembahasan:

Diketahui: 

N (jumlah lilitan) = 100 

A (luas penampang) = 0,005 m² 

ΔΦ (perubahan fluks magnetik) = 0,02 Wb 

Δt (perubahan waktu) = 0,1 detik

Jadi, hitung Hukum Faraday dalam menghitung rumus GGL Induksi (ε): 

ε = -N * ΔΦ / Δt 

ε = -100 * 0,02 Wb / 0,1 detik = -2 volt

Jadi, besar GGL induksi pada kumparan tersebut adalah 2 volt.

Sudah Paham Rumus GGL Insuksi? 

Demikianlah dalam artikel ini kita telah mempelajari berbagai rumus GGL induksi, konsepnya, faktor-faktor yang mempengaruhi besarnya GGL induksi, serta penerapannya dalam berbagai aspek kehidupan. 

Jadi, kita mengetahui bahwa GGL induksi adalah dasar bagi banyak teknologi modern dan menjadi inti dari induksi elektromagnetik. Semoga pengetahuan ini dapat memberikan pemahaman yang lebih mendalam tentang ilmu fisika dan aplikasinya dalam kehidupan sehari-hari.