Dalam ilmu matematika, operasi bilangan bulat adalah hal yang wajib untuk dipelajari. Adapun berdasarkan sifatnya, operasi bilangan bulat terbagi menjadi beberapa jenis, salah satunya yaitu sifat distributif. Artikel ini akan membahas pengertian, contoh hingga cara penyelesaian persamaan sifat distributif.
Pengertian Sifat Distributif

Sifat distributif adalah salah satu sifat operasi hitungan yang dalam penggunaannya menggunakan kombinasi penggabungan bilangan hasil operasi dengan elemen kombinasi yang ada. Selain itu, sifat ini juga digunakan untuk menyederhanakan suatu persamaan dengan menggunakan tanda kurung.
Atau dengan kata lain, sifat ini bisa membantu kamu dalam mengalikan suatu bilangan yang ada dalam tanda kurung dengan yang sedang kamu operasikan. Adapun rumus yang digunakan dalam sifat ini, yaitu:
a (b + c) = ab + bc
Catatan penting, yaitu jika tidak ada tanda hitung seperti “+”, “-”, “:”, atau “x”, maka itu berarti kamu harus menggunakan perkalian. Untuk itulah, persamaan tersebut jika lebih dirincikan menjadi seperti berikut:
a x ( b + c) = (a x b) + (a x c)
Cara Perhitungan Sifat Distributif dan Contohnya
Berikut ini beberapa cara perhitungan sifat ini lengkap dengan contohnya:
1. Distributif Perkalian Terhadap Penjumlahan
Untuk sifat distributif perkalian dengan penjumlahan, kamu bisa menggunakan rumus seperti berikut.
a x (b + c) = (a x b) + (a x c) = d
Keterangan:
a : bilangan yang didistribusikan
b : bilangan yang dikelompokkan
c : bilangan yang dikelompokkan
d : hasil dari operasi hitung
Adapun contoh soal dan penyelesaian sifat distributif perkalian terhadap penjumlahan sebagai berikut:
Soal 1
Berapakah hasil dari 4 (3 + 4) ?
Pembahasan:
4 (3 + 4) = (4 x 3) + (4 x 4) = 12 + 16 = 28
Soal 2
Berapakah hasil dari 5 (4 + 9) ?
Pembahasan:
5 (4 + 9) = (5 x 4) + ( 5 x 9) = 20 + 45 = 65
2. Distributif Perkalian Terhadap Pengurangan
Berikut ini rumus yang bisa kamu gunakan untuk menghitung soal berkaitan dengan distributif perkalian terhadap pengurangan
a x (b – c) = (a x b) – (a x c) = d
Berikut contoh soal dan penyelesaian sifat distributif perkalian terhadap pengurangan.
Soal 1
Berapakah hasil dari 6 (5 – 2) ?
Pembahasan:
6 (5 – 2) = (6 x 5) – (6 x 2) = 30 – 12 = 18
Soal 2
Berapakah hasil dari 6 (7 – 5) ?
Pembahasan:
6 (7 – 5) = (6 x 7) – (6 x 5) = 42 – 30 = 12
3. Distribusi Koefisien Negatif
Dalam perhitungan menggunakan sifat distributif, kamu akan menemukan beberapa bilangan dengan koefisien negatif. Adapun ketentuan perhitungan bilangan ini, yaitu:
- Bilangan Negatif x Bilangan Negatif = Positif
- Bilangan Negatif x Bilangan Positif = Negatif
Berikut ini beberapa contoh soal untuk perhitungan jenis ini:
Soal 1
Berapakah hasil dari -4 (9 − (-3)) ?
Pembahasan:
-4 (9 − (-3)) = -4 (9 + 3) = (-4 x 9) + (-4 x 3) = -36 – 12 = -48
Soal 2
Berapakah hasil dari 4 (-3 + 5) ?
Pembahasan:
4 x ( -3 + 5) = ( 4 x -3) + ( 4 x 5) = -12+20= 8
Soal 3
Berapakah hasil dari 7 (6 – (-5)) ?
Pembahasan:
7 (6 – (-5)) = ( 7 x 6 ) – ( 7 x -5) = 42 – (-35) = 42 + 35 = 77
4. Sifat Distribusi untuk Menyelesaikan Persamaan

Jika kamu memiliki soal berkaitan dengan persamaan, bisa menggunakan sifat distributif untuk menyelesaikannya. Adapun cara perhitungannya sebagai berikut:
a. Persamaan Dasar
Untuk menyelesaikan soal persamaan dasar dengan sifat ini, biasanya dengan mengalikan suku yang ada di luar tanda kurung dengan suku yang ada di dalam tanda kurung. Adapun contoh soalnya sebagai berikut:
Soal 1
Berapakah nilai x dari persamaan ini 2 (x – 3) = 10?
Pembahasan
2 (x – 3) = 10
2x – 6 = 10
2x = 16
x = 16/2 = 8
Jadi nilai x adalah 8.
Soal 2
Jika sebuah persamaan sebagai berikut: 2x (3 – 2) = 10, maka tentukan berapakah nilai x pada persamaan tersebut!
Pembahasan
2x (3 – 2) = 10
6x – 4x = 10
2x = 10
x = 10/2 = 5
Jadi nilai x adalah 5.
Soal 3
Perhatikan persamaan berikut:
3 (4 + 2x) = 18
Berapakah nilai x pada persamaan tersebut?
Pembahasan
3 (4 + 2x) = 18
12 + 6x = 18
6x = 18-12
x = 6/6 = 1
Jadi nilai x adalah 1.
b. Persamaan Pecahan
Sifat distribusi juga bisa kamu gunakan untuk menyelesaikan persamaan pecahan. Berikut ini beberapa contoh soal dan pembahasan berhubungan dengan distribusi dan persamaan pecahan:
Soal 1
Berapakah nilai x pada persamaan berikut ini:
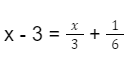
Pembahasan
Untuk menyelesaikan persamaan ini, hal pertama yang harus kamu lakukan adalah mengidentifikasi setiap pecahan dalam koefisien atau konstanta, kemudian cari kelipatan persekutuan terbesar KPK dari semua penyebut. Adapun untuk langkah penyelesaiannya lengkapnya, kurang lebih sebagai berikut:
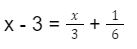
Kelipatan persekutuan terbesar dari penyebut adalah 6. Selanjutnya, kalikan pada setiap ruas, maka menjadi seperti ini:
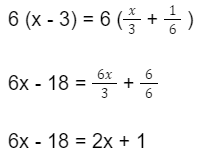
Selanjutnya, gabungkan setiap suku yang sama pada persamaan tersebut, seperti berikut:
(6x – 2x) = 18 + 1
4x = 19
Tahap terakhir, yaitu memecahkan persamaan tersebut, sehingga menjadi seperti berikut:
x = 19/4 = 4,75
Jadi nilai x adalah 4,75.
Soal 2
Berapakah nilai x dari persamaan berikut ini:
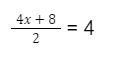
Pembahasan:
Untuk menyelesaikan persamaan tersebut, kamu bisa uraikan penyebut dari pecahan tersebut terlebih dahulu dan selesaikan dengan sifat distributif. Adapun hasilnya sebagai berikut:
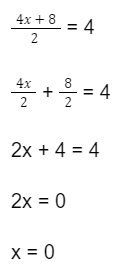
Jadi nilai x pada persamaan tersebut adalah 0.
c. Distribusi Persamaan Koefisien Negatif
Untuk mendistribusikan persamaan koefisien negatif, bisa kamu lakukan dengan 4 cara berikut ini.
- Distribusikan bilangan negatif dengan tanda negatif.
- Menyatukan suku-suku yang serupa.
- Melakukan pembagian guna memperoleh jawaban akhir.
- Memperlakukan tanda kurang dengan menambahkan -1.
Berikut contoh soal dan penyelesaian lengkap tentang distribusi persamaan koefisien negatif:
Soal
Berapakah nilai x dari persamaan berikut -4 (9 – 3x) = 48?
Pembahasan
Untuk menyelesaikan persamaan tersebut, bisa dengan mengikuti langkah-langkah pendistribusian persamaan koefisien negatif seperti yang sudah disebutkan sebelumnya. Berikut ini langkah penyelesaiannya secara lengkap.
-4 (9 – 3x) = 48 Distribusikan -4 pada tiap sukunya, sehingga menjadi seperti berikut:
-4 (9) – (-4) (3x) = 48
Selanjutnya, sederhanakan perkalian tersebut, sehingga menjadi:
-36 – (-12x) = 48
-36 + 12x = 48
Tahap berikutnya, kamu bisa menyederhanakan persamaan dengan memindahkan seluruh suku yang mengandung variabel pada sisi lainnya atau dengan memvariasikan penjumlahan atau pengurangan, sehingga hasilnya sebagai berikut:
-36 + (36) + 12x = 48 + (36) menambahkan angka 36 pada tiap sisinya, sehingga jika disederhanakan, hasilnya sebagai berikut:
12x = 84
Selanjutnya, kamu bisa memecahkan persamaan dengan cara membagi kedua sisi persamaan dengan koefisien yang ada di depan variabel. Adapun hasil dan penyelesaiannya sebagai berikut:
12x = 84 membagi kedua sisi dengan angka 12, sehingga seperti berikut:
12x/12 = 84/12
x = 7
Jadi, nilai x adalah 7.
Catatan penting dalam konsep ini, yaitu jika kamu menjumpai tanda negatif yang ada pada soal aljabar, maka bisa bayangkan angka tersebut sebagai + (-1). Cara ini akan sangat membantu kamu dalam menyelesaikan soal persamaan koefisien negatif dengan mudah.
Adapun contohnya yaitu 4x – (x + 2) = 4. Nah, kamu bisa menuliskannya dengan persamaan seperti berikut ini:
4x + (-1) (x + 2) = 4,
Lalu bisa langsung selesaikan persamaannya menjadi seperti berikut ini:
4x – x – 2 = 4
3x – 2 = 4
3x = 6
x = 2
Baca Juga : Sifat Asosiatif dalam Aljabar: Rumus dan Contoh Soalnya
Sudah Tahu Apa Itu Sifat Distributif?
Mengetahui sifat distributif sangat membantu dalam menghitung penjumlahan, pengurangan, dan perkalian suatu bilangan. Tanpa mengetahui sifat ini, maka kemungkinan kamu akan keliru dalam melakukan perhitungan bilangan. Ini adalah perhitungan yang sederhana, namun jika tidak mengetahui bagaimana aturan dalam perhitungannya, maka tentu saja kamu tidak bisa menyelesaikan suatu soal dengan benar. Untuk itulah, kamu juga perlu berlatih soal ini agar terbiasa dengan aturan hitungan dengan menggunakan sifat ini. Semoga membantu!

