Salah satu sifat yang dimiliki oleh operasi hitung bilangan yaitu sifat komutatif. Dalam ilmu matematika, operasi hitung bilangan memiliki 3 sifat yaitu sifat komutatif, asosiatif, dan distributif. Ketiga sifat tersebut memiliki metode penghitungan yang berbeda. Lalu apa pengertiannya? Bagaimana contoh dari sifat ini? Simak artikel ini sekarang juga!
Pengertian Sifat Komutatif
Sifat komutatif atau pertukaran dalam ilmu matematika dapat diartikan sebagai sifat operasi hitung terhadap dua bilangan yang memenuhi pertukaran letak antar bilangan. Kedua bilangan tersebut meskipun sudah ditukar, akan tetap menghasilkan hasil nilai yang sama.
Selain itu, sifat ini sering kali disebut dengan hukum komutatif. Artinya, suatu operasi hitung dapat disebut memiliki sifat komutatif jika letak bilangannya bisa saling ditukarkan tanpa mengubah hasil.
Sifat komutatif pada operasi hitung bilangan bertujuan untuk memudahkan proses perhitungan. Sifat ini juga membantu para siswa untuk lebih memahami operasi hitung pada bilangan secara menyeluruh. Dalam hal ini, operasi hitung berarti perkalian, pengurangan, penjumlahan, dan juga pembagian.
Jenis Sifat Komutatif

Tidak semua operasi hitung bisa menggunakan komutatif. Penggunaan sifat komutatif hanya bisa digunakan pada operasi hitung penjumlahan dan perkalian saja. Sehingga, operasi hitung pengurangan dan pembagian disebut sebagai operasi non komutatif. Agar lebih jelas, simak pembahasan berikut ini!
a. Sifat Komutatif dalam Penjumlahan
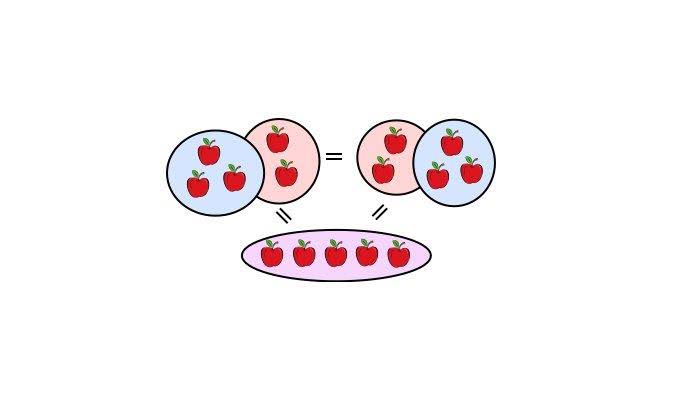
Operasi hitung bilangan penjumlahan yang menggunakan sifat komutatif berarti dua bilangan yang dijumlahkan memiliki hasil yang sama walaupun bilangan tersebut ditukar letaknya.
Adapun sifat komutatif pada operasi penjumlahan dapat dirumuskan sebagai berikut:
a + b = b + a = c
Keterangan:
a dan b = bilangan operasi hitung.
c = hasil operasi hitung penjumlahan.
1. Contoh pada penjumlahan dua bilangan positif
- 5 + 7 = 7 + 5 = 12, yang mana 5 + 7 = 12 dan 7 + 5 = 12
Terdapat angka 5 dan 7 yang jika dijumlahkan dengan posisi baik di depan maupun di belakang akan mendapatkan hasil nilai yang sama, yaitu 12.
2. Contoh pada penjumlahan bilangan negatif
- (-3) + 5 = 5 + (-3) = 2, maka (-3) + 5 = 2, dan 5 + (-3) = 2
- (-6) + (-5) = (-5) + (-6) = (-11), maka (-6) + (-5) = (-11) dan (-5) + (-6) = (-11)
Begitupun dengan contoh penjumlahan bilangan negatif. Hukum komutatif tetap berlaku untuk penjumlahan bilangan negatif yang mana tidak akan merubah hasil nilai.
b. Sifat Komutatif dalam Perkalian
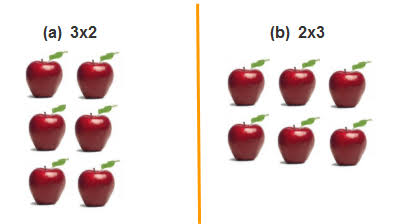
Selanjutnya, penerapan hukum komutatif dalam operasi hitung bilangan perkalian sama dengan yang ada pada penjumlahan. Sifat ini berlaku ketika dua bilangan bulat dikalikan dan posisinya ditukar menghasilkan hasil yang sama.
Berikut rumus sifat komutatif dalam perkalian:
a x b = b x a = c
Keterangan:
a dan b = bilangan operasi hitung.
c = hasil operasi hitung perkalian.
1. Hukum komutatif dalam perkalian bilangan positif dengan positif
Contoh:
- 2 x 5 = 5 x 2 = 10, yang berarti 2 x 5 = 10 dan 5 x 2 = 10
- 10 x 2 = 2 x 10 = 20, yang berarti 10 x 2 = 20 dan 2 x 10 = 20
Pada pola tersebut, terlihat jelas angka 2 dan 5 ketika dikalikan dan ditukar posisinya, hasilnya akan tetap sama. Demikian juga dengan angka 10 dan 2.
2. Hukum komutatif dalam perkalian bilangan negatif dengan positif
Contoh:
- (-5) x 3 = 3 x (-5) = (-15) yang berarti (-5) x 3 = (-15) dan 3 x (-5) = (-15)
- 4 x (-2) = (-2) x 4 = (-8) yang berarti 4 x (-2) = (-8) dan (-2) x 4 = (-8)
Pada contoh-contoh tersebut, perkalian dua bilangan bulat positif dan negatif akan mendapatkan hasil yang sama meskipun dengan perpindahan posisi sekalipun.
3. Hukum komutatif pada dua bilangan negatif
Contoh:
- (-3) x (-6) = (-6) x (-3) = (-18), yang berarti (-3) x (-6) = (-18) dan (-6) x (-3) = (-18)
- (-7) x (-4) = (-4) x (-7) = (-28), yang berarti (-7) x (-4) = (-28) dan (-4) x (-7) = (-28)
Terlihat dari contoh diatas yaitu kedua bilangan yang sama-sama negatif berlaku hukum komutatif dengan perubahan tempat yang tidak mengubah hasil.
c. Sifat Komutatif Tidak Berlaku dalam Pengurangan dan Pembagian
Mengapa operasi hitung pengurangan dan pembagian tidak dapat berlaku hukum komutatif? Sederhananya, jika dua bilangan dalam operasi pengurangan dan pembagian mengalami pertukaran posisi maka akan menghasilkan hasil yang berbeda.
Sehingga, hanya operasi hitung penjumlahan dan perkalian saja yang menghasilkan hasil yang sama meskipun posisi kedua bilangan mengalami pertukaran.
Jika hukum komutatif digunakan dalam operasi hitung pengurangan dan pembagian, maka rumusnya adalah:
a – b ≠ b – a
atau
a : b ≠ b : a
Perhatikan contoh berikut ini!
- 5 – 3 = 2 tidak sama dengan 3 – 5 = (-2)
Bilangan 5 – 3 hasilnya adalah 2, hasil ini tidak akan sama jika kedua bilangan tersebut mengalami perubahan posisi menjadi 3 – 5 yang hasilnya adalah (-2).
Contoh selanjutnya yaitu:
- 10 : 2 = 5 tidak sama dengan 2 : 10 = 0.2
Sama halnya dengan pengurangan. Kedua bilangan pada operasi hitung pembagian jika mengalami penukaran atau perubahan posisi baik di kanan maupun kiri, maka akan mendapatkan hasil yang berbeda. Seperti terlihat pada contoh, 10 : 2 hasilnya adalah 5, sedangkan 2 : 10 hasilnya akan berbeda yaitu 0.2.
Latihan Soal dan Pembahasan
Setelah mengetahui jenis dari hukum komutatif pada operasi hitung bilangan sekaligus rumus yang berlaku, saatnya untuk menguji kemampuanmu dengan latihan soal berikut ini. Latihan soal terdiri dari 20 soal dengan 10 soal sifat komutatif penjumlahan dan 10 soal sifat komutatif perkalian. Silakan dikerjakan sekarang juga.
Baca Juga : Sifat Asosiatif dalam Aljabar: Rumus dan Contoh Soalnya
A. Soal Sifat Komutatif Penjumlahan
Soal 1
37 + … = 73 + 37 = …
Jawaban: 37 + 73 = 73 + 37 = 110
Soal 2
115 + 250 = … + 115 = …
Jawaban: 115 + 250 = 250 + 115 = 365
Soal 3
… + 155 = 155 + 551 = …
Jawaban: 551 + 155 = 155 + 551 = 706
Soal 4
717 + 617 = 617 + … = …
Jawaban: 717 + 617 = 617 + 717 = 1.334
Soal 5
45 + 30 = … + … = 75
Jawaban: 45 + 30 = 30 + 45 = 75
Soal 6
65 + .. = 56 + … = …
Jawaban: 65 + 56 = 56 + 65 = 121
Soal 7
90 + 30 = … + … = …
Jawaban: 90 + 30 = 30 + 90 = 120
Soal 8
23 + … = … + 23 = 40
Jawaban: 23 + 17 = 17 + 23 = 40
Soal 9
… + 25 = 25 + … = 55
Jawaban: 30 + 25 = 25 + 30 = 55
Soal 10
11 + … = … + … = 20
Jawaban: 11 + 9 = 9 + 11 = 20
B. Soal Sifat Komutatif Perkalian
Soal 1
4 x 23 = … x 4 = …
Jawaban: 4 x 23 = 23 x 4 = 92
Soal 2
9 x … = 8 x 9 = …
Jawaban: 9 x 8 = 8 x 9 = 72
Soal 3
… x 13 = 13 x 4 = …
Jawaban: 4 x 13 = 13 x 4 = 52
Soal 4
8 x … = 15 x … = 120
Jawaban: 8 x 15 = 15 x 8 = 120
Soal 5
10 x … = … x 10 = 50
Jawaban: 10 x 5 = 5 x 10 = 50
Soal 6
… x 8 = 8 x … = 32
Jawaban: 4 x 8 = 8 x 4 = 32
Soal 7
21 x … = 4 x … = …
Jawaban: 21 x 4 = 4 x 21 = 84
Soal 8
5 x … = … x 5 = 40
Jawaban: 5 x 8 = 8 x 5 = 40
Soal 9
8 x … = … x … = 48
Jawaban: 8 x 6 = 6 x 8 = 48
Soal 10
… x 26 = 26 x … = 286
Jawaban: 11 x 26 = 26 x 11 = 286
Sudah Paham Mengenai Sifat Komutatif?
Itulah pembelajaran materi sifat komutatif yang merupakan salah satu sifat yang ada pada operasi hitung bilangan. Sifat komutatif atau pertukaran menjadi materi fundamental untuk mengerjakan soal-soal matematika lainnya. Banyaklah berlatih dan semoga artikel ini membantumu dalam memahami hukum matematika satu ini.

