Siswa SMA pasti sudah tidak asing lagi dengan materi trigonometri pada mata pelajaran Matematika. Banyak siswa merasa kesulitan saat mempelajari materi yang satu ini. Artikel ini akan mengupas salah satu sub materi dari trigonometri – sudut istimewa trigonometri. Ikuti, ya!
Apa itu Trigonometri?
Kamu perlu memahami tentang trigonometri lebih dulu sebelum mendalami materi tentang sudut istimewa trigonometri!
Trigonometri adalah salah satu cabang ilmu dari Matematika yang mempelajari tentang hubungan sisi dan sudut yang ada pada segitiga.
Jika selama ini kamu sudah belajar tentang segitiga dengan rumus Phytagoras, nah trigonometri ini adalah materi lebih lanjut yang akan memperdalam pemahamanmu tentang panjang dan sudut yang ada di segitiga.
Hubungan antara sisi dan sudut segitiga pada trigonometri dijelaskan dengan istilah sinus (sin), kosinus (cos), dan tangen (tan).
Hanya dengan tiga istilah itu, kamu bisa mencari panjang dari semua sisi segitiga meskipun hanya diketahui sudut dan salah satu panjang dari sisi segitiga.
Selain sinus (sin), kosinus (cos), dan tangen (tan), ada juga istilah lain yang terdapat pada trigonometri seperti kosekan (csc), sekan (sec), dan kotangen (cot).
Apa saja penjelasan lengkap dari semua istilah tersebut?
6 Istilah pada Trigonometri yang Perlu Kamu Ingat!
Simak penjelasan tentang istilah-istilah pada trigonometri yang harus kamu pahami dan ingat agar dapat memahami sudut istimewa trigonometri dengan lebih baik.
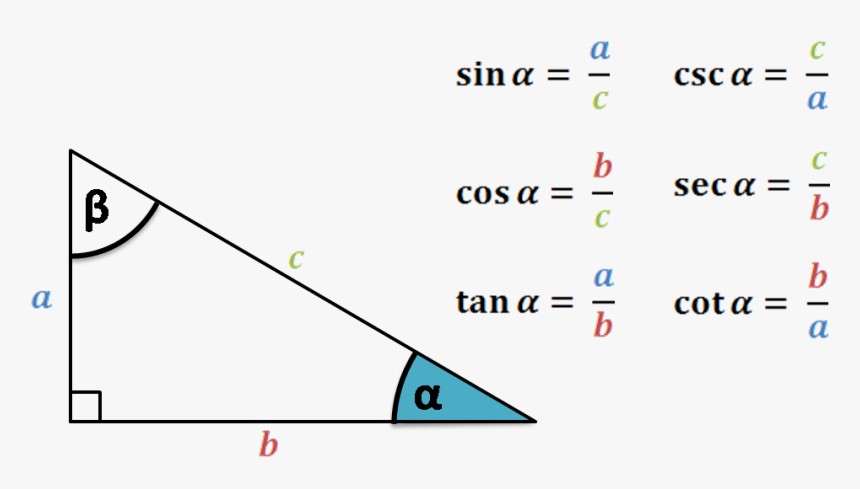
1. Sinus (sin)
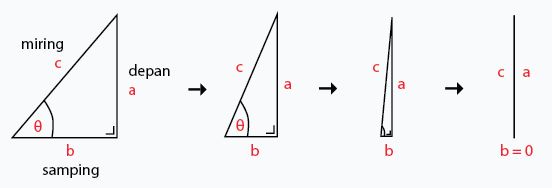
Sinus atau ‘sin’ merupakan perbandingan antara panjang sisi depan (a) dengan panjang dari sisi miring (c).
Jadi, rumusnya adalah ac.
2. Kosinus (cos)
Kosinus atau biasa disingkat ‘cos’ merupakan perbandingan panjang sisi samping (b) dengan panjang dari sisi miring (c). Rumusnya yaitu bc.
3. Tangen (tan)
Tangen atau disingkat ‘tan’ adalah perbandingan antara panjang dari sisi depan (a) dengan panjang dari sisi samping (b). Maka, rumus dari tangen adalah ab.
4. Kosekan (csc)
Kosekan atau bisa juga disingkat ‘csc’ adalah perbandingan antara panjang dari sisi miring (c) dengan panjang sisi depan (a). Bisa dibilang, kosekan ‘ ini adalah kebalikannya sinus.
Rumusnya sebagai berikut: ca atau 1sin .
5. Sekan (sec)
Selanjutnya ada sekan atau ‘sec’. Sekan adalah perbandingan antara panjang dari sisi miring (c) dengan panjang sisi samping (b), sehingga secan adalah kebalikan dari sinus (sin).
Rumus dari sekan yaitu cb atau 1cos .
6. Kotangen (cot)
Istilah terakhir dari trigonometri adalah kotangen. Istilah kotangen merupakan perbandingan panjang dari sisi samping (b) dengan panjang dari sisi depan (a). Kotangen adalah kebalikan dari tangen.
Rumus kotangen atau ‘cot’ adalah ba atau 1tan .
Sudut Istimewa Trigonometri
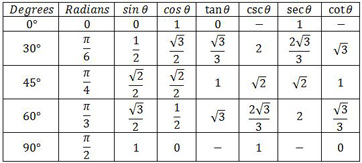
Jika kamu perhatikan, trigonometri sangat erat kaitannya dengan panjang dan sudut segitiga. Di dalam trigonometri, ada sejumlah sudut istimewa seperti 0°, 30°, 45°, 60°, dan 90°. Sudut tersebut dikatakan spesial karena dapat langsung ditemukan nilainya dari perhitungan rasio.
1. Sudut 0°
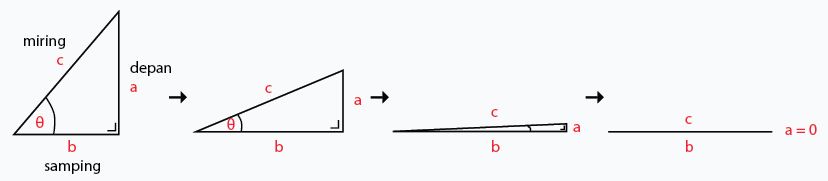
Konsep sudut istimewa 0° ini adalah membuat sudut sebesar 0° di sebuah segitiga siku-siku. Kalau kamu perhatikan gambar di atas, makin kecil sudutnya, panjang garis (a) akan semakin kecil.
Ketika saat sudut sudah mencapai 0°, panjang garis (a) sebesar 0 dan garis (b) menjadi satu garis lurus dengan garis (c). Dengan kata lain, garis (b) dan (c) sama panjangnya.
Dari konsep di atas, maka rumus dapat kamu gambarkan seperti berikut ini:
- sin θ = ac = 0
- cos θ = bc = 1
- tan θ = ab = 0
2. Sudut 30°
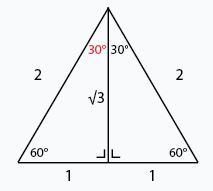
Sudut istimewa trigonometri 30° juga memiliki konsep pendekatan yang mirip dengan sudut di atas, yaitu dengan membuat sudut di sebuah segitiga siku-siku.
Namun, segitiga siku-siku ini awalnya diambil dari segitiga sama sisi. Kemudian, dibagi menjadi 2 segitiga siku-siku.
Segitiga siku-siku yang digunakan pada penjelasan konsep ini yaitu segitiga dengan nilai yang sederhana.
Sesuai dengan teorema Phytagoras. Jika sisi miringnya sepanjang 2 satuan, maka sisi alas sepanjang 1 satuan dan tinggi sepanjang 3.
Logikanya, jika ada sudut 30 derajat di segitiga siku-siku. Sudut ke-2 yang ada di segitiga tersebut adalah 90 derajat.
Perlu kamu ingat bahwa jumlah sudut dalam sebuah segitiga adalah 180°. Kalau sudut pertama adalah 30° dan yang kedua adalah 90° maka, sudut terakhir adalah 60°.
Dengan begitu, kesimpulannya adalah:
- sin θ = ac = 12
- cos θ = bc = 32 = 123
- tan θ = ab = 13 = 13 33 = 133
3. Sudut 45°
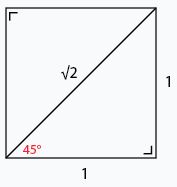
Sudut istimewa trigonometri 45° berawal dari persegi yang dibagi menjadi dua.
Menurut teorema Phytagoras, jika tinggi dan alasnya sama-sama sepanjang 1 satuan, maka panjang sisi sampingnya yaitu 2.
Dari hal ini, maka kamu bisa simpulkan bahwa:
- sin θ = ac = 12 = 12 22 = 122
- cos θ = bc = 12 = 12 22 = 122
- tan θ = ab = 11 = 1
4. Sudut 60°
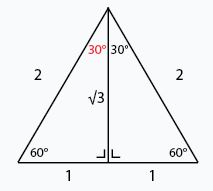
Untuk memahami konsep trigonometri sudut 60°, kita perlu ingat kembali pembahasan tentang sudut 30°. Konsep segitiga sama sisi yang akan dibagi menjadi 2 segitiga siku-siku juga berlaku di sini.
Jadi, kamu bisa melihat nilai dari sin, cos, tan sudut 60° adalah sebagai berikut:
- sin θ = ac = 32 = 123
- cos θ = bc = 12
- tan θ = ab = 31 = 3
5. Sudut 90°
Memahami konsep sudut istimewa trigonometri 90° sebetulnya sama saja saat kita memahami konsep dari sudut 0°.
Kalau kamu perhatikan gambar di atas, kamu harus memperpendek panjang sisi (b) ika kamu ingin membentuk sudut θ. Makin besar sudut yang terbentuk, makin pendek panjang sudut (b).
Ketika sudut sudah menyentuh 90°, sisi (b) akirnya sepanjang 0 satuan dan panjang garis (a) dan © sama.
Nah, dengan demikian, kamu memperoleh rumus sebagai berikut:
- sin θ = ac = 1
- cos θ = bc = 0c = 0
- tan θ = ab = 10 = Tidak terdefinisikan (TD)
Contoh Soal Sudut Istimewa Trigonometri
Nah, sekarang kita bisa masuk ke contoh soal agar kamu punya pemahaman yang lebih baik tentang materi sudut istimewa trigonometri. Sudah siap?
1. Hitunglah tan 45° + cos 30°
2. Hitunglah sin 30° + tan 60°
3. Buktikan jika cos245° + sin245° = 1
Pembahasan
1. tan 45° + cos 30° = 1 + 123 = 12 (3 + 2)
2. sin 30° + tan 60° = 12 + 3 = 12 (1 + 23)
3. cos245° + sin245° = (122)2 + (122)2 = (14×2) + (14×2) = 12 + 12 = 1
Apa Pengaruhnya Memahami Sudut Istimewa Trigonometri ?
Sulit dibantah jika banyak siswa yang merasa materi trigonometri dalam Matematika adalah momok menakutkan karena materi-materinya terkenal sulit dimengerti. Akan tetapi, memahami dasar dan konsep dari trigonometri, termasuk tentang sudut istimewa trigonometri, akan sangat membantumu dalam menyelami trigonometri secara utuh. Bahkan, pemahaman tentang materi yang satu ini juga dapat memfasilitasi kamu menguasai beberapa cabang ilmu sains yang terkait ke depannya!