Bola adalah bentuk yang sangat penting dalam berbagai aspek kehidupan manusia, baik dalam aspek olahraga, sebagai elemen desain arsitektur, atau bahkan sebagai model matematika. Sejak dahulu, para ahli matematika akan menghitung ukuran tertentu pada bola menggunakan rumus bola.
Dalam artikel ini, kita akan belajar bersama berbagai rumus bola, termasuk cara menghitung luas permukaan, keliling, dan volume bola. Selain itu, kami akan memberikan contoh soal yang menantang beserta solusinya untuk membantu Anda memahami konsep-konsep bola dengan lebih baik.
Apa Itu Bola?
Dalam konsep matematika, bola adalah salah satu bentuk geometris berupa benda bulat yang memiliki bangun ruang tiga dimensi. Aspek yang membedakannya dari lingkaran adalah bahwa bola didefinisikan oleh tiga sumbu, yaitu sumbu x, y, dan z.
Bangun ruang bola termasuk benda padat tiga dimensi yang memiliki dua ukuran penting, yaitu luas permukaan dan volume. Mirip seperti lingkaran, setiap titik di bola memiliki jarak yang sama dari tengahnya.
Semua titik pada permukaan bola memiliki jarak yang konstan dari pusatnya. Artinya, tidak peduli dari mana Anda mengukurnya, jaraknya akan selalu sama. Konsep ini dikenal dengan istilah jari-jari bola. Kemudian, diameter adalah jarak dari satu titik di permukaan bola ke titik lainnya yang mana melewati pusatnya.
Luas permukaan bola adalah wilayah yang terliputi oleh permukaan bola, sedangkan volume bola adalah jumlah ruang yang terisi oleh benda bulat ini. Singkatnya, rumus bola adalah bentuk tiga dimensi dengan luas permukaan dan volume yang penting.
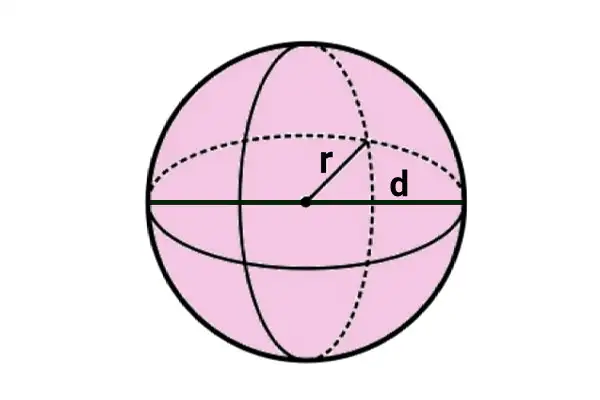
Pada gambar di atas, terlihat sebuah bola memiliki jari-jari “r”. Berbeda dengan lingkaran yang terbatas pada bidang datar XY, bola memiliki dimensi tiga, yaitu sepanjang sumbu x, y, dan z.
Karateristik Bola
Bangun ruang bola memiliki sejumlah karakteristik khas yang nantinya akan mengacu pada perhitungan rumus bola, diantaranya adalah:
- Bola hanya memiliki satu sisi, yaitu permukaannya. Permukaan bola adalah himpunan semua titik yang memiliki jarak yang sama dari pusat bola.
- Lantaran hanya memiliki satu sisi, bola tidak memiliki rusuk atau garis perpotongan antara dua sisi.
- Jari-jari bola (dengan singkatan r) adalah garis yang menghubungkan pusat bola ke titik di permukaannya.
- Bola memiliki diameter yang merujuk pada dua kali panjang jari-jarinya, sama seperti pada bangun datar lingkaran.
- Bola juga memiliki garis lurus yang menghubungkan dua titik di permukaan bola, namanya tali busur bola. Tali busur bola terpanjang adalah diameter bola.
Persamaan Bola
Dalam ilmu matematika atau geomertri analitik, Anda bisa menggambarkan persamaan sebuah bola sebagai berikut:
“Jika terdapat jari-jari dengan nilai “r”, maka lokasi titik-titik dalam bangun tiga dimensinya adalah sebagai (x, y, z), sedangkan pusat bola adalah sebagai (x0, y0, z0)”. Sehingga, persamaan bola dapat direpresetasikan sebagai berikut:
(x -x0)² + (y – y0)² + (z-z0)² = r²
Rumus Bola
Seperti yang telah kita bahas sebelumnya, bola memiliki beberapa karakteristik penting, seperti volume, luas permukaan, dan jari-jari, yang dapat Anda hitung menggunakan rumus-rumus berikut:
1. Rumus Luas Permukaan Bola
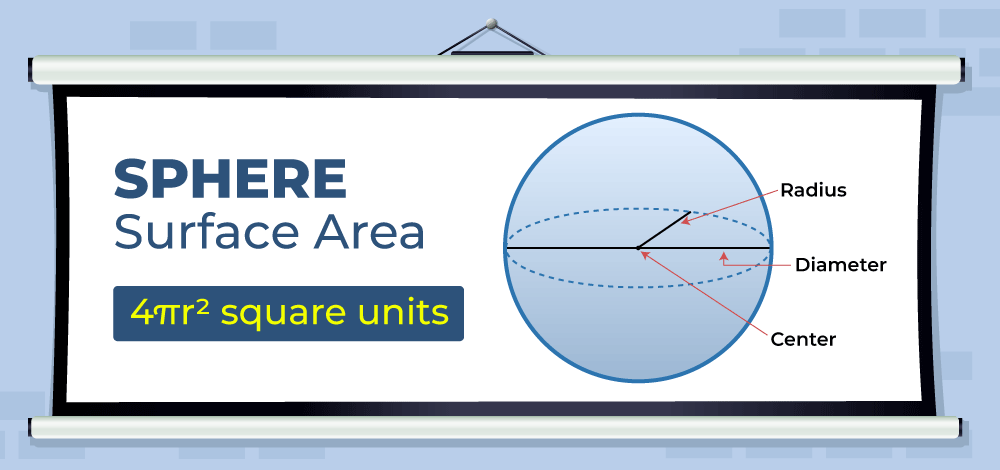
Luas permukaan bola adalah jumlah total area yang diliputi oleh permukaan bola dalam tiga dimensi. Rumus untuk menghitung luas permukaan adalah sebagai berikut:
Luas permukaan bola = 4 x π x r², dalam unit persegi.
Dalam rumus bola tersebut, r adalah panjang jari-jari bola. Sedangkan π (phi) adalah konstanta matematika yang memiliki nilai 3,14.
2. Rumus Keliling Bola
Rumus untuk menghitung keliling sebuah bangun ruang bola adalah:
K = (4/3) x π x r²
3. Rumus Volume Bola

Prinsip Archimedes menjelaskan bahwa volume dari objek tiga dimensi yang menyebutnya bola dapat Anda hitung dengan rumus berikut:
Volume Bola (V) = (4/3) x π x r³, dalam unit kubik.
Dalam rumus tersebut, V merupakan volume, r adalah panjang jari-jari, dan π adalah konstanta dengan nilai sekitar 3,14.
Baca Juga : Rumus Limas Segitiga Beserta Contoh Soal dan Pembahasan
Contoh Soal dan Pembahasan Rumus Bola
Mari kita bahas beberapa contoh soal dan pembahasannya yang menggunakan rumus-rumus bola di bawah ini:
1. Contoh 1
Ahmad ingin menggantikan ban mobilnya yang bocor. Diameter ban tersebut adalah 10 cm. Berapa volume ban yang perlu Ahmad isi dengan udara?
Jawaban:
Untuk menghitung volume ban, Anda perlu menggunakan rumus volume bola. Diketahui diameter ban adalah 10 cm, sehingga jari-jarinya (r) adalah setengah dari diameter, yaitu 5 cm.
Menggunakan rumus volume, Anda dapat menghitung volume ban:
Diketahui diameter, d = 10 cm.
Kita tahu bahwa jari-jari, r = d / 2 = 10 / 2 = 5 cm.
Untuk menghitung volume, kita gunakan rumus bola untuk volumenya:
V = (4/3) x π x r³.
Maka, V = (4/3) × (22/7) × 5³ = 522 cm³
Jadi, volume ban yang harus diisi Ahmad dengan udara adalah 522 cm³.
2. Contoh 2
Maya memiliki bola yang memiliki jari-jari sepanjang 7 cm. Kemudian, Maya ingin menghias bola tersebut dengan stiker. Berapa luas permukaan bola yang perlu Maya siapkan untuk menempelkan stiker?
Jawaban:
Untuk menghitung luas permukaan bola, Anda perlu menggunakan rumus bola yaitu luas permukaan bola. Diketahui jari-jari bola adalah 7 cm. Menggunakan rumus luas permukaan bola, Anda dapat menghitung luas permukaan bola:
Dengan jari-jari, r = 7 cm.
Anda gunakan rumus luas permukaan bola = 4 x π x r²
Maka, luas = 4 × (22/7) × 7² = 616 cm²
Jadi, luas permukaan bola yang perlu disiapkan Maya untuk menempelkan stiker adalah 616 cm².
3. Contoh 3
Rudi memiliki bola yang memiliki jari-jari sepanjang 9 cm. Rudi ingin tahu berapa volume bola tersebut dalam notasi π. Bantu Rudi menghitung volume bola tersebut. Berapa volume bola dalam notasi π jika jari-jarinya adalah 9 cm?
Jawaban:
Untuk menghitung volume bola dalam notasi π, Anda dapat menggunakan rumus volume bola. Dengan mengetahui jari-jari bola adalah 9 cm, maka Anda dapat menghitung volume bola:
Jari-jari, r = 9 cm.
Anda gunakan rumus volume: V = (4/3) x π x r³
Maka, V = (4/3) × π × 9³ = 972π cm³
Jadi, volume bola dalam notasi π jika jari-jarinya adalah 9 cm adalah 972π cm³.
4. Contoh 4
Pada suatu lapangan olahraga, terdapat sebuah bola voli dengan permukaan yang sangat halus. Tim bola voli lokal ingin mengukur keliling bola voli tersebut.
Mereka mengetahui bahwa jari-jari bola voli adalah 16 cm. Bantu tim tersebut menghitung keliling bangun ruang bola voli ini.Berapa keliling bangun ruang bola voli tersebut?
Jawaban:
Untuk menghitung keliling bola voli, Anda bisa menggunakan rumus bola yakni keliling bola, yaitu K = (4/3) x π x r², yang mana r adalah jari-jari bola voli.
Dalam kasus ini, r = 16 cm. Sekarang, Anda substitusi nilai r ke dalam rumus tersebut:
K = (4/3) x π x (16 cm)²
K = (4/3) x π x (256 cm) = (1024/3)π cm²
Jadi, keliling bangun ruang bola voli tersebut adalah (1024/3)π cm² atau sekitar 1072,76 cm².
Sudah Paham dengan Semua Rumus Bola?
Dalam kesimpulannya, bola adalah bangun ruang yang menarik dengan karakteristik unik dalam ilmu geometri yang ada. Berbagai rumus bola telah membantu kita memahami dan memodelkan sifat-sifat bola serta menerapkannya dalam berbagai bidang pengetahuan.
Sebut saja dalam ilmu fisika, rumus-rumus bola di atas dapat membantu perhitungan massa jenis bola, momentum bola, dan energi kinetik bola. Rumus-rumus tersebut bisa menjadi dasar dalam pemahaman tentang energi dalam berbagai jenis pergerakan bola, seperti pergerakan planet dalam astronomi.
Meskipun bola adalah bentuk yang sederhana, mereka sangatlah penting dalam banyak aspek kehidupan kita. Ingatlah bahwa matematika adalah alat penting dalam ilmu pengetahuan dan berbagai bidang kehidupan. Teruslah belajar dan eksplorasi, dan jangan ragu untuk mencari tahu lebih lanjut tentang topik matematika lainnya.

