Titik berat trapesium merupakan bagian yang tidak dapat terpisahkan dalam studi bangun trapesium pada matematika. Peranannya pun cukup penting dalam berbagai bidang di kehidupan sehari-hari.
Titik berat pada bangun ini jarang orang ketahui karena merupakan tahapan studi lanjut terhadap trapesium. Yuk, simak pembahasannya berikut ini beserta beberapa contoh soal yang dapat Anda jadikan referensi.
Apa Itu Bangun Trapesium?
Menurut Kamus Besar Bahasa Indonesia (KBBI), trapesium merupakan bangun segi empat yang kedua sisinya berdiri sejajar, namun tidak memiliki panjang yang sama.
Apabila Anda perhatikan secara seksama, bangun trapesium juga dapat terbentuk dari bangun segitiga siku-siku dan bangun persegi.
Bangun ini termasuk sebagai bangun berbentuk persegi panjang dengan simetri rotasi. Trapesium memiliki sisi sejajar dan sisi yang tidak sejajar. Bagian sisi yang sejajar memiliki panjang yang sama. Sedangkan, sisi yang tidak sejajar panjangnya berbeda.
Penerapan bangun trapesium dalam kehidupan sehari-hari sangatlah beragam. Salah satu contohnya, pada atap rumah. Mayoritas atap rumah, terutama yang tradisional memiliki bentuk trapesium, yakni dengan kedua sisi yang sejajar dan kedua sisi lainnya tidak sejajar.
Tidak hanya pada atap, juga banyak benda lainnya yang berbentuk dan menerapkan titik berat trapesium dalam pembuatannya.
Baca Juga : Rumus Persegi Panjang: Luas, Keliling, serta Contoh Soal
Sifat Bangun Trapesium
Bangun trapesium memiliki beberapa sifat khusus, diantaranya adalah sebagai berikut.
- Terdapat berbagaI bentuk trapesium, yaitu trapesium sama kaki, trapesium siku-siku, dan trapesium sembarang.
- Sudut pada segitiga sama kaki yang saling berseberangan memiliki besaran yang sama.
- Pada bagian tengahnya terdapat sebuah garis yang membagi kedua sisi trapesium menjadi dua buah segitiga sama kaki.
- Titik berat trapesium adalah titik potong pada garis tengah yang membaginya.
- Memiliki dua buah sisi yang sejajar dan dua buah sisi yang tidak sejajar.
- Pada trapesium siku-siku dan trapesium sembarang memiliki dua diagonal yang tidak sama panjangnya.
- Memiliki sebuah sudut tumpul pada bangun trapesium siku-siku.
- Pada bangun trapesium sembarang, memiliki empat buah sudut yang besarannya berbeda.
Jenis Bangun Trapesium
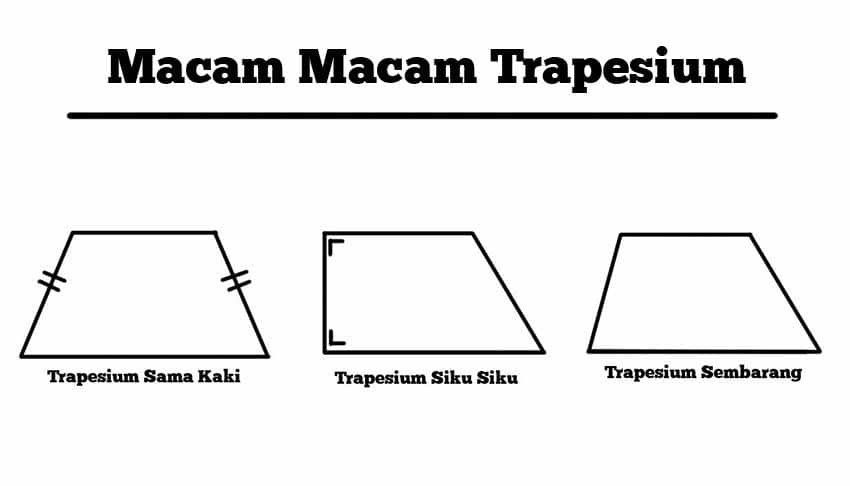
Seperti yang telah sebelumnya sebutkan, terdapat tiga jenis bangun trapesium. Adapun ketiga jenis tersebut antara lain adalah sebagai berikut.
1. Trapesium Sembarang
Trapesium sembarang merupakan bangun trapesium yang keempat sisinya memiliki panjang berbeda. Bentuk ini juga tidak memiliki sudut siku-siku.
Selain itu, trapesium sembarang tidak memiliki simetri lipat karena bentuk garisnya yang berbeda, tetapi tetap memiliki simetri putar.
2. Trapesium sama kaki
Jenis selanjutnya adalah trapesium sama kaki. Trapesium sama kaki memiliki dua sisi yang saling sejajar. Apabila ditarik garis tengah, akan terbentuk dua buah bangun segitiga sama kaki.
Berbeda dengan sebelumnya, jenis ini memiliki simetri lipat dan simetri putar atau yang biasa disebut simetri rotasi.
3. Trapesium siku-siku
Trapesium siku-siku merupakan bangun trapesium yang memiliki dua sudut siku-siku yang saling berdekatan. Pada bangun ini terdapat sudut lancip, namun tidak terdapat simetri lipat. Meski demikian, trapesium siku-siku memiliki simetri putar.
Pengertian Titik Berat Trapesium
Sebelumnya sempat disebutkan, titik berat trapesium merupakan titik pusat pada garis potong trapesium. Apabila didefinisikan secara terpisah, titik berat merupakan titik pusat yang terdapat pada setiap benda dan berorientasi pada gravitasi.
Pada dasarnya, setiap benda merupakan susunan dari partikel-partikel yang memiliki massa. Gabungan massa tersebutlah yang berpusat pada gravitasi yang seringkali dikatakan sebagai titik berat.
Begitu halnya dengan bangun trapesium. Titik berat pada bangun ini adalah pusat orientasinya.
Rumus Titik Berat Trapesium
Adapun rumus-rumus yang perlu Anda pelajari dalam menghitung titik berat trapesium adalah sebagai berikut.
1. Luas Trapesium
Secara umum, untuk menghitung luas trapesium Anda dapat menggunakan rumus berikut:
L = ½ × panjang total sisi-sisi yang sejajar × t
atau
L = ½ (a+b) t
2. Keliling Trapesium
K= AB + BC + CD + DA
3. Tinggi (t)
t = 2x L(a+b)
4. Sisi a (CD)
a = 2x Lt– b
Atau
CD = K – AB – BC – AD
5. Sisi b (AB)
b = 2x Lt– a
Atau
AB = K – CD – BC – AD
6. Sisi AD
AD = K – CD – BC – AB
7. Sisi BC
BC = K – CD – AD – AB
8. Momen Luas
Sebelum menghitung titik berat, perlu untuk menghitung momen luasnya terlebih dahulu menggunakan rumus berikut:
Mx = (1/2)t (a+c)/2 (a+c)/2 My = (1/3)t [(2b+a)/(a+b)] [(a+c)/2]
9. Titik Berat
Rumus yang dapat Anda gunakan untuk menghitung titik berat pada berbagai jenis trapesium, yaitu:
x = (a + c)/2 y = (t/3) x [(2b + a)/ (a + b)]
4 Aplikasi Titik Berat Trapesium dalam Kehidupan Sehari-hari
Dalam kehidupan sehari-hari, penerapan titik berat trapesium ternyata memiliki peranan yang penting. Beberapa penerapannya mayoritas berguna untuk membangun suatu gedung atau dalam pembuatan sebuah logo. Berikut 4 contoh penerapannya, yaitu:
1. Desain Bangunan
Dalam proses perencanaan suatu bangunan, titik berat trapesium dapat membantu menentukan kestabilan struktur bangunannya. Penggunaannya berguna untuk menentukan pondasi yang tepat dalam sebuah bangunan.
Perhitungan titik berat dapat membantu seorang arsitek dengan tepat dan aman untuk menentukan struktur bangunan.
2. Pemrograman Robotik
Fungsi selanjutnya dalam kehidupan sehari-hari adalah dalam pemrograman robotik. Khususnya untuk membuat robot dapat bergerak dengan lancar dan stabil.
Perhitungan titik berat pada program robotik berguna untuk merancang sistem pengendalian yang tepat, sehingga pergerakan robot menjadi stabil.
3. Olahraga
Olahraga, terutama tinju juga memanfaatkan titik berat trapesium. Perhitungan ini dalam olahraga berguna untuk menentukan strategi yang tepat dalam menghadapi lawannya.
Selain tinju, olahraga basket juga memanfaatkan peranan titik berat. Fungsinya untuk mengetahui sudut yang tepat saat melempar bola ke ring.
4. Tas Tangan
Apabila Anda perhatikan secara seksama, banyak tas tangan yang menggunakan bentuk trapesium sebagai desainnya.
Pada bagian tepi atas dan bawah memiliki garis yang sejajar, sementara bagian sampinnya tidak. Mayoritas bentuk yang digunakan adalah trapesium sama kaki.
Baca Juga : Memahami Ciri dan Sifat Bangun Datar serta Pembahasannya
Contoh Soal dan Pembahasannya
Berikut 2 contoh soal tentang titik berat trapesium lengkap beserta pembahasannya, yaitu:
Contoh Soal 1
Sebuah trapesium sama kaki memiliki panjang alas atas 4 cm, panjang alas bawah 10 cm, dan tinggi 6 cm. Berapakah titik berat trapesium tersebut?
Diketahui:
AB (Alas atas) = 4 cm
CD (alas bawah) = 10 cm
t = 6 cm
Jawab:
Bagi bangun trapesium menjadi empat bagian dan hitung setiap momen luasnya terlebih dahulu sebagai berikut.
M1 = 1/2 x 6 x 4 x 4 = 48 cm³
M2 = 1/2 x 6 x 4 x 2 = 24 cm³
M3 = 1/2 x 6 x 4 x 8 = 96 cm³
M4 = 1/2 x 6 x 4 x 10 = 120 cm³
M Total = M1 + M2 + M3 + M4 = 48 + 24 + 96 + 120 = 288 cm³
Luas Trapesium (A) = 1/2 x 6 x (4 + 10) = 42 cm²
x = M / A = 288 / 42 = 6,8 cm
Contoh Soal 2
Tentukan koordinat titik berat bidang trapesium berikut.
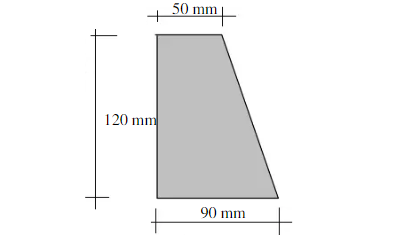
Jawab :
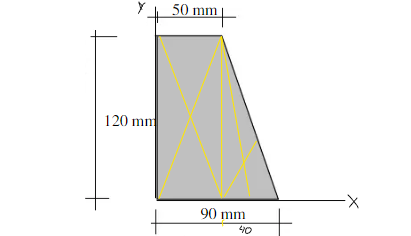
Bidang 1 (Persegi)
X = Luas 1. x1 = (pxl). (½ b) = (50×120) (½ 50) = 6000 x 25 =150.000
Y = Luas 1. y1 = 6000 (½ h) = 6000 (½ 120) = 6000 × 60 = 360.000
Bidang 2 (segitiga)
X = Luas 2. x2 = (½ at) (⅓ b) = (½ × 120× 40) (⅓ × 40 + 50) = 2400. 63,3 = 151.920
Y = Luas 2. y2 = 2400 (⅓ 120) = 2400 × 40 = 96.000
Jadi koordinat titik berat trapesium adalah
X = X1 + X2Luas 1 + Luas 2 = 150000 + 1519206000 + 2400= 3019208400 = 35,94
Y = Y1 + Y2Luas 1 + Luas 2 = 360000 + 960006000 + 2400= 4560008400 = 54,28
Sudah Tahu Bagaimana Menentukan Titik Berat Trapesium?
Banyak faktor yang perlu dipahami untuk menentukan titik berat trapesium seperti luas, keliling, panjang sisi, dan momen luasnya. Dengan demikian akan ditemukan hasil yang akurat.
Pasalnya penerapan titik berat bangun ini dalam kehidupan sehari-hari memiliki peranan penting, terutama dalam menentukan pondasi suatu bangunan. Banyaknya faktor tersebut akan meminimalisir kesalahan pada perhitungan, sehingga dalam pengaplikasiannya lebih aman dan terjamin.

