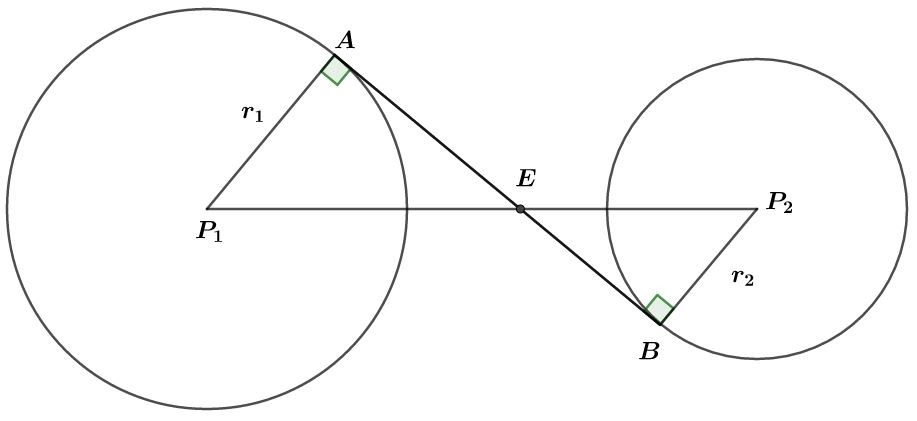
Rumus garis singgung persekutuan dalam adalah salah satu konsep penting dalam matematika. Fungsi dari rumus ini adalah untuk memahami hubungan antara dua lingkaran atau kurva.
Artikel ini akan membahas tentang garis singgung persekutuan tersebut secara lebih mendalam beserta rumus dan contoh soal untuk memahaminya lebih baik. Yuk, simak dengan seksama!
Pengertian Garis Singgung Lingkaran
Garis singgung lingkaran merupakan garis yang bersentuhan atau memotong lingkaran pada satu titik spesifik di permukaan lingkaran tersebut.
Dalam garis singgung terdapat titik singgung. Titik singgung sendiri merupakan titik pertemuan dengan objek atau bentuk yang bersentuhan dengannya.
Garis ini memiliki sifat khusus yang penting dalam geometri dan matematika. Umumnya, garis singgung sering digunakan dalam berbagai hal seperti perhitungan jarak, konstruksi geometris, dan pemecahan masalah matematika.
Ada dua jenis garis singgung lingkaran. Pertama, garis singgung luar, yakni garis yang menyentuh kedua lingkaran secara eksternal. Garis ini tidak memotong atau memasuki bagian lingkaran manapun. Panjang garis singgung luar ini sama dengan jari-jari lingkaran.
Kedua, garis singgung dalam, yakni garis yang menyentuh kedua lingkaran secara internal. Pada garis ini juga tidak memotong atau memasuki bagian lingkaran mana pun. Panjang garis singgung dalam ini juga sama dengan jari-jari lingkaran.
Karakteristik Garis Singgung Lingkaran
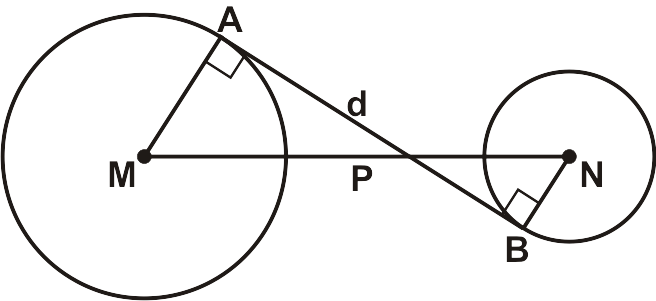
Adapun karakteristik garis singgung pada lingkaran adalah sebagai berikut.
- Garis singgung lingkaran hanya bersentuhan atau memotong lingkaran tepat di satu titik.
- Jika menarik garis dari titik di luar lingkaran, Anda dapat membuat dua garis singgung yang berbeda.
- Garis singgung selalu berada dalam posisi sejajar dan tegak lurus terhadap jari-jari lingkaran di titik singgungnya.
- Sudut 90 derajat akan terbentuk ketika garis singgung dan jari-jari lingkaran dalam posisi sejajar
- Panjang garis singgung yang menghubungkan satu titik di luar lingkaran ke titik singgung adalah sama.
Rumus Garis Singgung Persekutuan Dalam
Untuk menghitung panjang garis singgung lingkaran, Anda harus memahami dengan baik konsep dan rumus yang terkait dengan teorema Pythagoras.
Sebelumnya, coba perhatikan gambar di bawah ini!
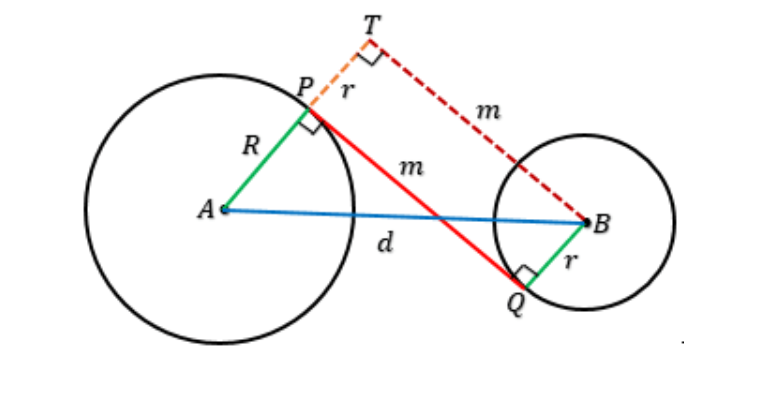
Lingkaran besar A memiliki jari-jari panjang R. Sementara itu, lingkaran kecil B memiliki jari-jari r.
Garis AP dan garis BQ tegak lurus terhadap garis PQ, sehingga garis PQ menyentuh kedua lingkaran dan selalu membentuk sudut tegak lurus dengan garis singgung di titik kontak.
Dengan kata lain, garis PQ merupakan Garis Singgung Persekutuan Dalam (GSPD) kedua lingkaran A dan B. Jarak antara pusat lingkaran besar A dan pusat lingkaran kecil B adalah AB = d.
Panjang garis PT sama dengan panjang garis BQ, dan keduanya sejajar, sehingga PT = BQ = r. Garis PQ juga sejajar dan memiliki panjang yang sama dengan garis BT, sehingga PQ = BT = m.
Di dalam garis singgung lingkaran persekutuan mencakup dua lingkaran dan garis singgung lingkaran. Segitiga ABT adalah segitiga siku-siku dengan sudut siku-siku berada di T, sehingga kita dapat menggunakan rumus Pythagoras sebagai berikut.
AB2=AT2+BT2
BT2=AB2−AT2
PQ2=AB2−AT2
Panjang garis BT yang sama dengan panjang garis PQ, maka:
AT =AP+PT
=R+r
AB =dPQ
Sehingga:
m2=d2−(R+r)2
m=√d2−(R+r)2
Keterangan:
m = panjang garis singgung persekutuan dalam dua lingkaran.
d = jarak antara pusat lingkaran besar dan pusat lingkaran kecil.
R = jari-jari lingkaran besar.
r = jari-jari lingkaran kecil.
R lebih besar dari r.
4 Contoh Soal dan Pembahasannya
Untuk memahaminya lebih dalam, Anda perlu meluangkan waktu untuk mempelajari contoh soal beserta pembahasannya. Adapun contoh-contoh soal untuk mengaplikasikan rumus garis singgung persekutuan dalam sebagai berikut.
Contoh Soal 1
Dua lingkaran memiliki jari-jari masing-masing 2 cm dan 7 cm. sementara itu, jarak antara pusat kedua lingkaran yakni 15 cm. Hitunglah panjang garis singgung persekutuan dalam kedua lingkaran dan pilih jawaban yang benar di bawah ini!
A. 12 cm
B. 10 cm
C. 9 cm
D. 8 cm
Pembahasan:
Jarak antara pusat kedua lingkaran adalah d=15 cm.
Jari-jari lingkaran besar adalah R=7 cm.
Jari-jari lingkaran kecil adalah r=2 cm.
m =√d2−(R+r)2
=√152−(7+2)2
=√152−92 =√225−81
m =√144 =12
Sehingga, panjang garis singgung persekutuan dalam kedua lingkaran tersebut yakni 12 cm. Jawaban yang benar adalah A.
Contoh Soal 2
Diketahui panjang jari-jari dua lingkaran adalah 12 cm dan 5 cm. sementara jarak antara kedua titik pusatnya adalah 24 cm. Hitung panjang garis singgung persekutuan dalamnya!
Pembahasan:
Pertama identifikasi nilai-nilai yang telah diberikan:
Jari-jari lingkaran pertama R = 12 cm
Jari-jari lingkaran kedua r = 5 cm
Jarak antara kedua pusat lingkaran k = 24 cm
Kemudian gunakan rumus garis singgung persekutuan dalam:
d = √(k² – (R + r)²)
= √(24² – (12 + 5)²)
= √(576 – (17)²) = √(576 – 289)
d = √287 = 16,94
Panjang garis singgung persekutuan dalam kedua lingkaran tersebut adalah 16,94 cm.
Contoh Soal 3
Diketahui adanya dua lingkaran dengan jari-jari masing-masing 14 cm dan 4 cm. Coba tentukan panjang garis singgung persekutuan kedua lingkaran tersebut apabila jarak kedua titik pusatnya 30 cm!
Pembahasan:
Jari-jari lingkaran pertama R = 14 cm
Jari-jari lingkaran kedua r = 4 cm
Jarak antara kedua titik pusat lingkaran k = 30 cm
d = √(k² – (R + r)²)
= √(30² – (14 + 4)²)
= √(900 – (18)²) = √(900 – 324)
d = √576 = 24
Dapat disimpulkan bahwa panjang garis singgung persekutuan dalam (d) kedua lingkaran tersebut yakni 24 cm.
Contoh Soal 4
Diketahui terdapat dua lingkaran, di mana jari-jari lingkaran pertama (R) adalah 5 cm dan jari-jari lingkaran kedua (r) adalah 3 cm. Jarak antara kedua pusat lingkaran (k) adalah 10 cm. Hitunglah panjang garis singgung persekutuan yang ada dalam kedua lingkaran tersebut.
Pembahasan:
Jari-jari lingkaran pertama R = 5 cm
Jari-jari lingkaran kedua r = 3 cm
Jarak antara kedua titik pusat lingkaran k = 10 cm
d = √(k² – (R + r)²)
= √(10² – (5 + 3)²)
= √(100 – (8)²) = √(100 – 64)
d = √36 = 6
Sehingga dapat disimpulkan bahwa panjang garis singgung persekutuan dalam (d) kedua lingkaran tersebut yakni 6 cm.
Baca Juga : Persamaan Garis Lurus: Pengertian, Sifat, Rumus, dan Soal
Sudah Paham Rumus Garis Singgung Persekutuan Dalam?
Dalam perhitungan menggunakan rumus garis singgung persekutuan dalam, faktor utama yang diperlukan jari-jari kedua lingkaran dan jarak antara kedua pusat lingkaran. Rumus ini dapat Anda gunakan untuk memecahkan masalah geometri yang melibatkan lingkaran dan garis singgungnya.
Penting untuk diingat, pemahaman teori saja tidak cukup. Anda juga perlu berlatih dengan berbagai contoh soal terkait. Dengan berlatih, Anda mampu mengimplementasikan rumus tersebut dengan baik.