Integral adalah salah satu konsep penting dalam kalkulus yang mana merupakan cabang bidang ilmu matematika yang berkaitan dengan perubahan suatu fungsi. Sebut saja rumus integral yang berguna dalam menentukan berbagai besaran seperti perpindahan, luas, dan volume.
Penasaran bagaimana rumus integral dapat digunakan dalam berbagai konteks? Yuk, pahami pengertian hingga penggunaannya dalam berbagai contoh soal dengan membaca artikel ini sampai selesai!
Apa Itu Integral?
Perhitungan integral bermanfaat untuk menemukan fungsi dalam penentuan suatu variabel seperti luas, perpindahan, dan volume yang ada karena kumpulan data yang kecil, sehingga tidak dapat terukur secara tunggal.
Dalam istilah yang lebih teknis, integral adalah antiderivatif sebagai kebalikan dari fungsi turunan atau diferensiasi. Sebagai contoh, terdapat f(x) = x2. Apabila Anda menghitung fungsi turunannya dari f(x), maka f'(x) = 2x atau dapat dimisalkan sebagai g(x).
Dengan nilai g(x)= 2x, nilai integralnya adalah menjadi ∫g(x) =x2. Dari persamaan tersebut terbukti bahwa fungsi integral adalah kebalikan dari fungsi turunan.
Kemudian, aturan umum penerapan rumus integral untuk mempermudah pemahaman Anda dalam menghitung kalkulus adalah jika terdapat persamaan xn , maka penyelesaian integralnya adalah dengan cara:
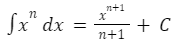
Sebagai contoh, apabila nilai n = 3, maka:
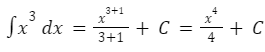
Jenis-Jenis Integral
Secara teori, terdapat dua jenis integral yang paling umum digunakan, yaitu:
1. Integral Tentu (Definite Integral)
Jenis integral ini memiliki nilai batas yang sudah ada sebelumnya. Rumus integral untuk jenis integral tentu terdapat fungsi (f) dari variabel riil (x) dengan interval [a,b]. Oleh karena itu, apabila dituliskan persamaannya, maka akan menjadi sebagai berikut:
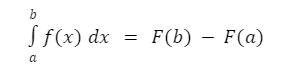
Keterangan:
- ∫ = simbol integral
- a = batas bawah integral
- b = batas atas integral
- f(x)= nilai fungsi
- F(a) = nilai integral untuk x sama dengan a
- F(b) = nilai integral untuk x sama dengan b
Menurut matematikawan Bernhard Riemann, integral tentu mengacu pada pembatas yang mendekati luas wilayah lengkung dengan memecah wilayah menjadi lempengan vertikal tipis.
Di sisi lain, teorema dasar integral ini adalah sebagai fungsi area yang dibatasi oleh kurva y = f (x), a <= x <= b, sumbu x, dan koordinat x = a dan x = b, yang mana b > a.
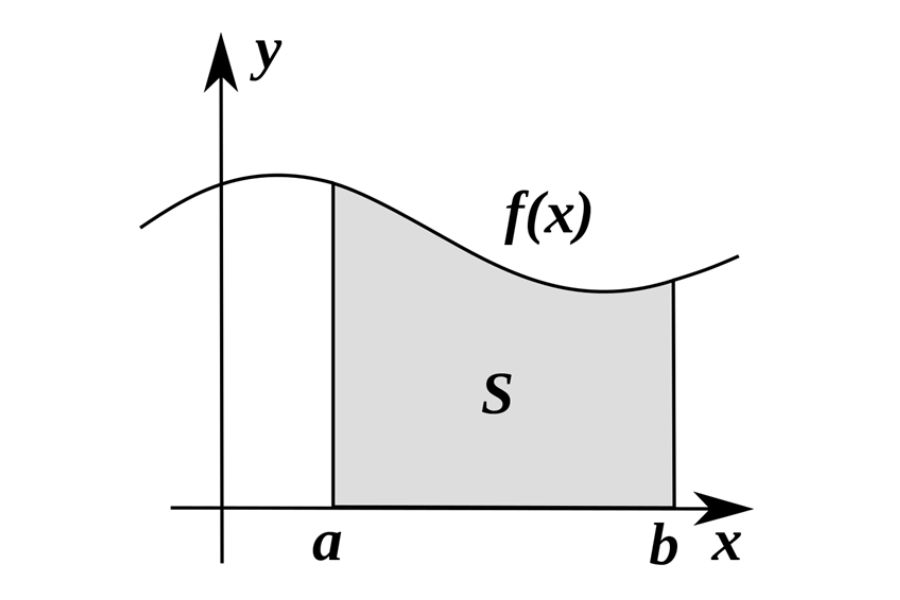
Secara sederhana, apabila ada nilai antiderivatif F untuk interval [a,b], maka integral tentu dari fungsi tersebut adalah perbedaan nilai pada titik a dan b. Berikut ini adalah beberapa rumus integral untuk sifat-sifat integral tentu yang akan membantu Anda dalam memahami perhitungan kalkulus secara lebih efisien:
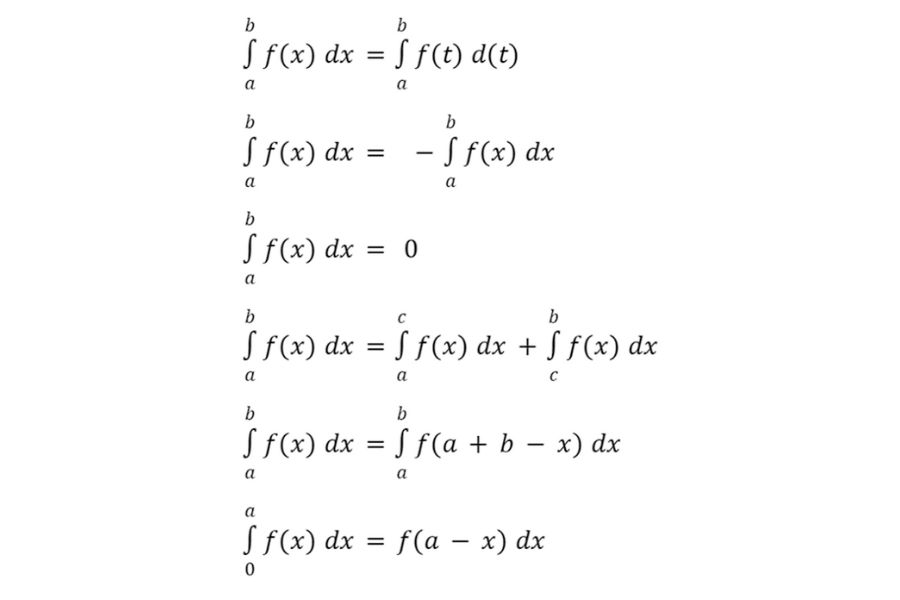
2. Integral Tak Tentu (Indefinite Integral atau Antiderivative)
Berbeda dengan integral tentu, jenis integral tak tentu tidak memiliki batas. Oleh karena itu, nilai akhir dari integral tak tentu menjadi tidak terbatas. Rumus integral untuk jenis ini adalah ∫f(x) dx = F(x) +C, di mana C adalah konstanta dalam fungsi f(x).
Perbedaan integral tentu dengan integral tak tentu dapat Anda lihat pada hasil akhirnya. Dalam integral tentu, hasil akhirnya adalah suatu nilai atau bilangan riil. Sedangkan integral tak tentu, hasil akhirnya masih dalam bentuk fungsi matematika.
Namun, selain kedua integral di atas, para ahli juga membagi jenis-jenis integral khusus sebagai berikut:
3. Rumus Integral Pecahan
Integral pecahan adalah jenis integral yang melibatkan pemecahan fungsi pecahan yang kompleks, sehingga bisa menjadi fungsi yang lebih sederhana. Secara matematis, integral pecahan dapat dituliskan dalam bentuk berikut:
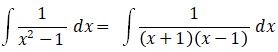
4. Integral Eksponensial
Integral eksponensial adalah jenis integral yang melibatkan fungsi eksponensial, yaitu fungsi yang memiliki bentuk ex, di dalam operasi integral. Dalam notasi matematika, integral eksponensial sering dituliskan sebagai:
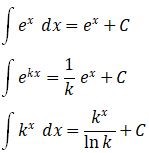
5. Integral Substitusi
Singkatnya, integral substitusi yang juga dikenal sebagai metode penggantian variabel merupakan salah satu teknik penting dalam kalkulus untuk menyelesaikan integral kompleks dengan menggantikan variabel dalam integral.
6. Rumus Integral Parsial
Terakhir, integral parsial adalah teknik untuk mengintegrasikan produk dari dua fungsi. Teknik ini berguna saat Anda memiliki integral dari fungsi-fungsi yang tidak mudah diintegrasikan secara langsung.
Tetapi ketika produk dari dua fungsi tersebut dapat diintegrasikan, Anda akan mengambil turunan dari salah satu fungsi dan mengambil integral dari yang lain. Adapun persamaan integral parsial adalah:
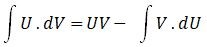
Rumus Integral
Berikut ini beberapa rumus integral yang mana umumnya berguna dalam perhitungan matematika yang lebih kompleks. Dengan menggunakan rumus ini, Anda bisa lebih mudah menyelesaikan persoalan apa pun yang terkait dengan integral:

Baca Juga : Rumus Integral Parsial Lengkap dengan Soal dan Pembahasan
Contoh Soal Penerapan Rumus Integral
Berikut beberapa contoh soal lengkap dengan pembahasan untuk memperdalam pemahaman Anda terkait rumus integral:
1. Contoh Soal 1
Hitung integral tak tentu dari ∫6x5-18x2+7 dx!
Pembahasan:
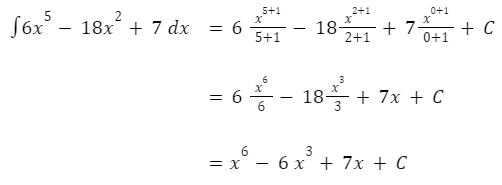
Setelah penyederhanaan, integral tak tentu untuk 6x5 – 18x2 + 7 adalah x6 – 6x3 + 7x + C.
2. Contoh Soal 2
Tentukan integral dari e3x!
Pembahasan:
f(x)=e3x
Berdasarkan rumus integral, nilai dari:
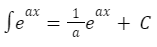
Oleh sebab itu:
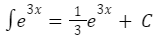
3. Contoh Soal 3
Diketahui terdapat persamaan integral sebagai berikut:
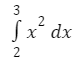
Hitung persamaan integral tersebut!
Pembahasan:
Pertama-tama, abaikan terlebih dahulu nilai batas bawah dan batas atas integral tersebut.
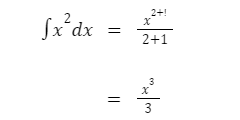
Setelah menghitung nilai integralnya, langkah selanjutnya adalah mensubstitusikan nilai batas a = 3 dan b = 2 terhadap persamaan:
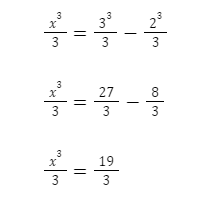

4. Contoh Soal 4
Diketahui terdapat persamaan integral sebagai berikut:
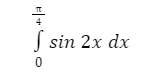
Tentukan nilai integralnya!
Pembahasan:
Sekarang, hitung ∫sin 2x dx terlebih dahulu. Berdasarkan rumus integral, maka:
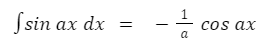
Berdasarkan rumus di atas, maka:
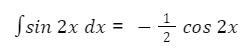
Kemudian, masukkan nilai batas integral ke persamaan berikut:
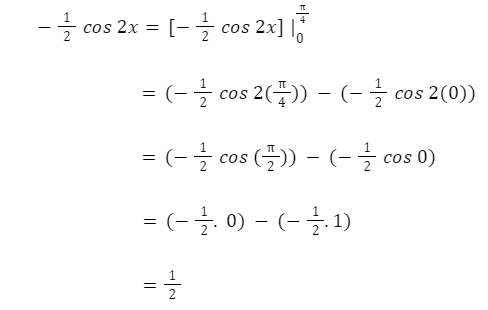

5. Contoh Soal 5
Selesaikan integral tentu dari:
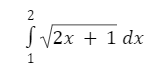
Pembahasan:
Pertama, lakukan permisalan u = 2x + 1. Oleh sebab itu, du = dx. Dari permisalan tersebut, ganti nilai-nilainya pada persamaan di atas, sehingga menjadi:
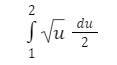
Langkah selanjutnya, abaikan nilai-nilai batas integral terlebih dahulu.
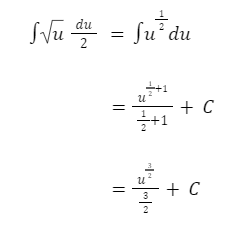
Hasil integralnya menjadi:
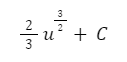
Berikutnya, gantilah nilai u dengan fungsi aslinya, sehingga menjadi:
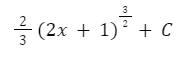
Bagian selanjutnya, substitusikan nilai batas integral ke persamaan. Dengan menggunakan rumus integral:
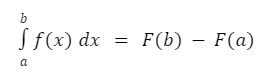
Maka:
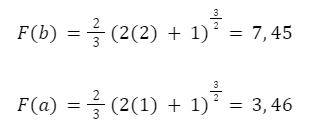
Jadi:
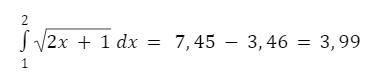
Yuk, Pahami Pentingnya Mempelajari Rumus Integral!
Dalam artikel ini, kita telah membahas rumus integral dan memberikan contoh soal serta pembahasannya. Ingatlah bahwa pemahaman konsep rumus integral adalah dasar penting dalam kalkulus matematika dan bidang lain seperti teknik, fisika, dan ilmu pengetahuan.
Dalam bidang ilmu fisika, integral berguna untuk menghitung luas, volume, dan berbagai parameter lain yang terkait dengan perubahan suatu besaran terhadap waktu atau ruang. Perhitungan ini memungkinkan Anda untuk mengukur sejumlah besar fenomena fisik, seperti perpindahan, kecepatan, dan percepatan.
Selain itu, dalam ekonomi dan statistik, integral digunakan untuk menghitung probabilitas, mengukur kurva permintaan, dan menganalisis data ekonomi. Sedangkan dalam ilmu teknik dan teknologi, integral digunakan untuk merancang struktur, menghitung aliran fluida, dan menganalisis sinyal dalam sistem komunikasi.
Integral adalah salah satu konsep matematika paling dasar dan penting yang pernah ada hingga saat ini. Memahami integral adalah langkah penting dalam memahami dasar-dasar matematika dan aplikasinya dalam dunia nyata. Selamat belajar!

