Rumus Integral Parsial Lengkap dengan Soal dan Pembahasan

Dalam ilmu matematika, materi integral dibagi menjadi dua berdasarkan tekniknya, yaitu integral parsial dan integral substitusi. Kedua integral ini hampir sama, perbedaannya yakni pada cara dan komponen yang diintegrasikan. Pada artikel ini akan fokus membahas rumus integral parsial yang lengkap dengan soal dan pembahasannya!

Integral Parsial

Sebelum menguraikan rumus integral parsial, sebaiknya  ketahui dulu pengertiannya. Adapun integral parsial merupakan suatu teknik pengintegralan dengan cara parsial, yang mana dengan pemisahan, karena komponen yang diintegrasikan memuat variabel yang sama, tetapi berbeda fungsinya. 

Biasanya, jenis integral ini orang gunakan untuk menyelesaikan suatu persamaan yang kompleks. Selain itu, cara ini juga biasanya digunakan ketika cara substitusi tidak berhasil dalam menyelesaikan permasalahan matematika.

Rumus Integral Parsial

Pada dasarnya, bentuk rumus umum dari integral parsial sebagai berikut:

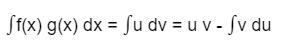
Adapun rumus tersebut diperoleh dari persamaan berikut ini:

u = f(x) jadi du = f(x) dx

dv = g(x) dx dari v = g(x) dx

Namun, jika f(x) berupa polinom derajat n ≥ 1, n ∈ asli, maka bentuk formula tersebut bisa disederhanakan seperti skema berikut:

Adapun tabel tersebut maksudnya, yaitu kolom fungsi f(x) di sebelah kiri adalah fungsi yang diturunkan hingga turunannya bernilai 0. Sedangkan jika kolom fungsi g(x) atau yang sebelah kanan harus diintegralkan sampai kolom sebelah kiri bernilai 0. 

Selain itu, tanda fungsi tersebut selalu berselang-seling, yaitu dari positif (+) menjadi negatif (-) dan seterusnya. Untuk itulah, lebih lanjut rumus integral tersebut bisa kamu tulis juga sebagai berikut: 

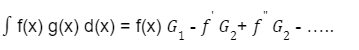
Tidak hanya itu, rumus integral parsial juga bisa dibagi menjadi dua tipe, yaitu integral tak tentu dengan integral tentu. Adapun rumus untuk integral parsial tak tentu sebagai berikut:

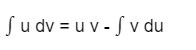
Sedangkan rumus untuk integral parsial tentu, yaitu:

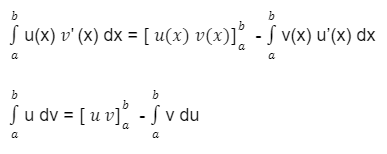
Baca Juga : Integer Adalah: Pengertian, Ukuran, dan Contoh Penggunaannya

Contoh Soal Integral Parsial dan Pembahasan

Untuk lebih jelasnya mengenai penjelasan rumus integral parsial tersebut, berikut ini contoh soalnya lengkap dengan pembahasan:

Soal 1

Berapakan hasil integral dari ʃ x2 cos x dx? 

Pembahasan:

Pertama-tama kita misalkan bahwa:

ʃ x cos x dx = ʃ u dv

Maka, kamu bisa mengetahui bahwa:

u = x, jadi diperoleh du = 1 dx

dv = cos x dx, jadi diperoleh v = sin x

Selanjutnya, distribusikan 4 variabel tersebut, sehingga diperoleh penyelesaian sebagai berikut:

ʃ x cos x dx = ʃ u dv

ʃ x cos x dx = uv – ʃ v du

Lalu,

ʃ x cos x dx = x (sin x) – ʃ sin x (1 dx)

ʃ x cos x dx = x sin x – ʃ sin x dx

Sederhanakan lagi menjadi,

ʃ x cos x dx = x sin x – (-cos x)

ʃ x cos x dx = x sin x + cos x

Jadi hasil akhirnya adalah x sin x + cos x.

Soal 2

Tentukan, berapakah hasil integral dari persamaan berikut ini:

ʃ Inxdx

Pembahasan:

Adapun bentuk soal tersebut bisa kamu selesaikan dengan metode dasar, karena tidak memiliki polinom derajat dari bilangan aslinya. Selanjutnya, kamu bisa misalkan rumusnya untuk mulai menyelesaikan soal tersebut. 

Misal:

u = Inx, maka du = 1/x dx

dv = dx, maka v = x

Selanjutnya, kamu bisa mulai memasukkannya ke dalam persamaan seperti berikut:

ʃ Inx dx = u v – ʃ v du

ʃ Inx dx = (Inx (x) – ʃ x (1/x dx)

Kemudian, sederhanakan menjadi:

ʃ Inx dx = x Inx – ʃ dx

ʃ Inx dx = x Inx – x + c

Maka, hasil integral dari Inx dx adalah x Inx – x + c.

Soal 3

Tentukan berapakah integral dari:

ʃ 2x (5x + 1)⁶ dx

Pembahasan:  

Pertama, misalkan 2x = u, jadi 2 dx = du

Kemudian, misalkan juga dv = (5x + 1)⁶ dx, 

maka v = (1/5) (1/7) (5x + 1)⁷ = 1/35 (5x + 1)⁷

Jadi, penyelesaian untuk soal tersebut sebagai berikut:

ʃ 2x (5x + 1)6 dx = 2x (1/35) (5x + 1)2 – 1/35 (5x + 1)7 2 dx

          = 2x/35 (5x + 1)⁷ – 2/35 (1/5) (1/8) (5x + 1)⁸ + c

          = 2x/35 (5x + 1)⁷ – 1/700 (5x + 1)⁸ + c

Maka, hasil integral dari ʃ 2x (5x + 1)⁶ dx adalah 2x/35 (5x + 1)⁷ – 1/700 (5x + 1)⁸ + c.

Soal 4

Berapakah hasil integral dari :

ʃ x (x + 4)⁵ dx 

Pembahasan:

Hal yang pertama untuk menyelesaikan soal tersebut adalah dengan membuat permisalan sebagai berikut:

u = x, maka du = dx

dv = (x + 4)⁵ dx, maka v = 1/6 (x + 4)⁶

Dengan menggunakan rumus integral parsial, maka penyelesaiannya sebagai berikut:

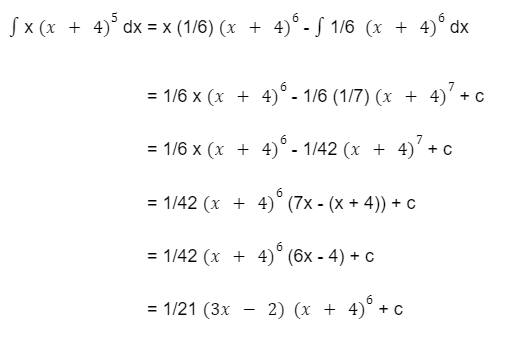
Jadi hasil integral dari

ʃ x (x + 4)⁵ dx  adalah 1/21 (3x – 2)(x + 4)⁶ + c.

Soal 5

Berapakah hasil dari

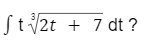
Pembahasan:

Untuk menyelesaikan soal tersebut, kamu bisa misalkan terlebih dahulu:

u = x, maka du = dx

dv = (x + 4)⁵ dx, maka v = 1/6  (x + 4)⁶

Selanjutnya, dengan menggunakan rumus integral parsial, kamu bisa menyelesaikannya seperti berikut:

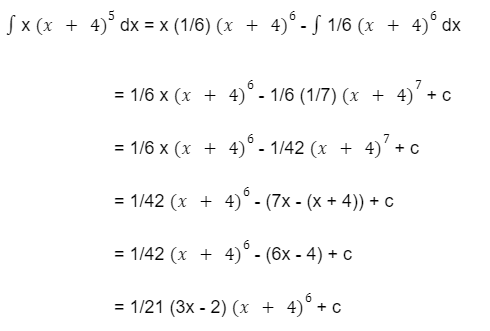
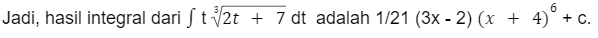
Sudah Tahu Rumus Integral Parsial? 

Untuk menghitung integral parsial memang tidak semudah yang dibayangkan. Mengingat rumusnya yang cukup banyak dan sangat rumit, sehingga memerlukan tenaga ekstra untuk memikirkan cara menyelesaikan soalnya. 

Namun dengan berlatih secara rutin dan terstruktur, maka tidak ada yang tidak mungkin untuk bisa menyelesaikan soal integral ini. Kamu bisa berlatih menggunakan beberapa soal di atas atau mencari soal yang lain dan berlandaskan pada pembahasan tersebut. Semoga membantu!