Tahukah kamu, cermin ternyata masih ada kaitannya dengan ilmu matematika? Karena terdapat peristiwa pencerminan atau refleksi yang dapat diketahui melalui suatu persamaan umum secara matematis. Nah, rumus pencerminan transformasi geometri bisa menunjukkan hasil atau bayangannya.
Selain itu, kamu tentu sudah memahami jika jarak antara bayangan dan cermin pasti selalu sama dengan jarak kamu dan cermin. Semakin kamu menjauh dari cermin, tentu bayanganmu akan semakin kecil yang terlihat. Jadi, untuk mengetahui lebih jelas peristiwa ini dalam ilmu matematika, simak ulasan selengkapnya di bawah ini!
Pengertian Pencerminan dalam Transformasi Geometri
Transformasi geometri merupakan perubahan posisi dan ukuran suatu objek pada bidang geometri, seperti titik, garis, dan kurva.
Transformasi ini dapat dituliskan dalam bentuk koordinat Cartesius dan matriks, lantaran memiliki garis dan titik. Lebih lanjut, ada banyak jenis transformasi geometri yang bisa kamu pelajari, seperti refleksi, translasi, rotasi, dan dilatasi.
Apakah kamu pernah bercermin dan mengamati bayanganmu di cermin? Nah, itu adalah salah satu contoh transformasi geometri berupa refleksi. Refleksi atau pencerminan merupakan perpindahan titik suatu objek pada bidang berdasarkan sifat pembentukan bayangan pada cermin datar.
Rumus Pencerminan Transformasi Geometri
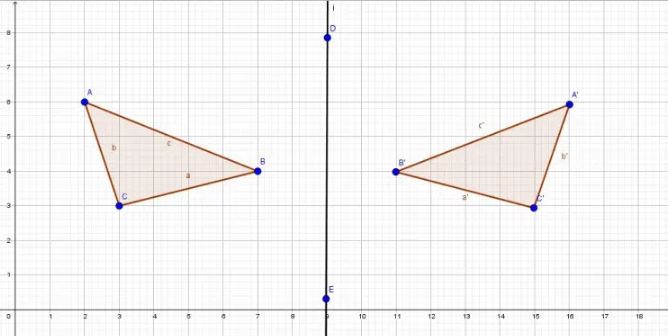
Pencerminan bisa kamu lakukan terhadap sumbu X maupun sumbu Y, mengingat kedua sumbu ini dapat dianalogikan sebagai cermin. Persamaan umum dari pencerminan dapat diketahui dalam berbagai rumus, seperti berikut:
1. Refleksi Terhadap Sumbu Y
Koordinat X’ adalah lawan dari koordinat X dengan koordinat Y tetap, apabila terjadi pencerminan terhadap sumbu Y. Secara matematis, berikut ini rumus untuk menentukan hasil pencerminannya:
P(x, y) menjadi P(-x, y)
Keterangan:
P(x, y) = titik koordinat awal
P’(-x, y) = titik koordinat akhir
2. Refleksi Terhadap Sumbu X
Apabila sumbu X diibaratkan sebagai cermin, maka koordinat y’ adalah lawan dari koordinat y, dimana koordinat x tetap. Rumus pencerminan transformasi geometri terhadap sumbu X adalah:
(x, y) menjadi (x, -y)
Keterangan:
P(x, y) = titik koordinat awal
P’(x, -y) = titik koordinat akhir
3. Refleksi Terhadap Garis Y = X
Selain terhadap sumbu x dan sumbu y, refleksi juga dapat dilakukan pada suatu objek terhadap garis. Refleksi terhadap garis Y = X dapat diketahui melalui rumus berikut:
P(x, y) menjadi P’(y, x)
4. Refleksi Terhadap Garis Y = -X
Apabila suatu titik P dengan koordinat (x, y) direfleksikan terhadap garis y = -x, maka menghasilkan koordinat P’(-y, -x). Jadi, rumus pencerminan transformasi geometri pada garis ini adalah:
P(x, y) menjadi P’(-y, -x)
Keterangan:
X’ = -y dan Y’ = -x
5. Refleksi Terhadap Garis Y = k
Adapun rumus pencerminan transformasi geometri pada titik P(x, y) terhadap garis y = k, maka menghasilkan koordinat P’(x, (2k – y)). Jadi, rumus refleksi pada garis ini adalah:
(x, y) menjadi (x, (2k – y))
6. Refleksi Terhadap Garis X = h
Apabila terdapat pencerminan terhadap garis x = h pada titik P dengan koordinat (x, y), maka akan menghasilkan koordinat P’((2h -x), y). Jadi, rumus refleksi pada garis ini adalah:
P(x, y) menjadi P’(2h -x, y)
7. Refleksi Terhadap Titik Asal 0 (0, 0)
Terakhir, persamaan umum untuk pencerminan dalam transformasi geometri adalah refleksi terhadap titik asal 0 (0, 0). Rumus refleksi terhadap titik asal, yaitu:
(x, y) menjadi (-x, -y)
Sifat-Sifat Pencerminan
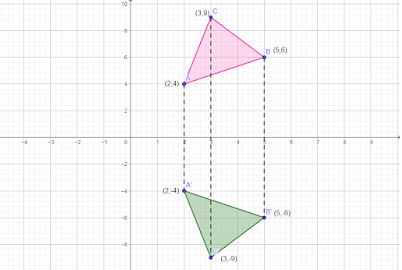
Setelah mengetahui rumus pencerminan transformasi geometri, kamu mungkin sudah mendapatkan gambaran sifatnya. Refleksi memiliki prinsip pergeseran, hampir sama dengan translasi. Bedanya, pencerminan mempunyai sifat tertentu yang menunjukkan posisi akhir objek sebagai hasil pencerminan dari objek awal. Berikut ini sifatnya:
- Terdapat sumbu X atau sumbu Y yang dianalogikan sebagai pusat refleksi atau cermin.
- Jarak antara titik awal objek ke cermin dan jarak titik akhir objek ke cermin adalah sama.
- Garis penghubung antara objek awal dan objek akhir selalu tegak lurus dengan cermin. Apabila suatu objek dicerminkan terhadap sumbu X, maka garis penghubungnya tegak lurus dengan sumbu X. Begitupun pencerminan terhadap sumbu Y.
Contoh Soal dan Pembahasan
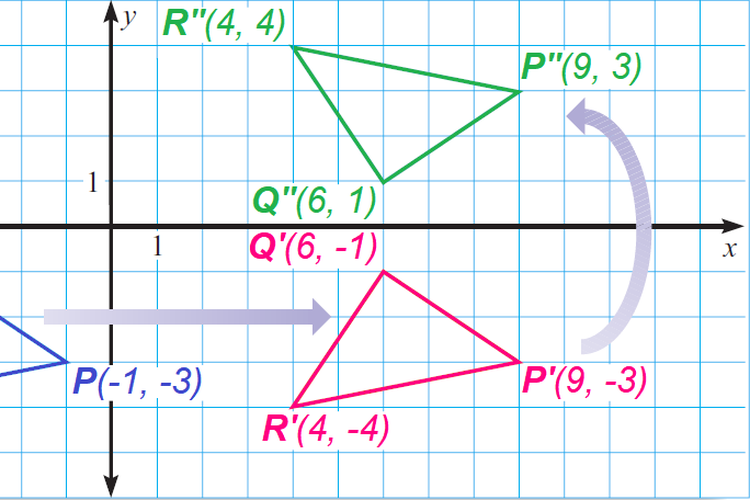
Berikut beberapa contoh dari penerapan rumus pencerminan transformasi geometri beserta pembahasannya:
Contoh 1
Tentukanlah koordinat bayangan (A’) dari titik A (4, -2), dicerminkan terhadap sumbu X.
Pembahasan:
A= (a,b) maka A’ (a, -b)
A= (4, -2) maka A’ (4, 2)
Jadi, koordinat bayangan dari titik A adalah (4, 2).
Contoh 2
Tentukan titik A’, jika titik A adalah (4, -2) terhadap garis X = -5!
Pembahasan:
Untuk menyelesaikan soal ini, gunakan rumus garis X = h.
(x, y) = (2H – x, y)
(4, -2) = (2(-5) – 4, -2)
= (-14, -2)
Jadi, titik A’ berada pada koordinat (-14, -2).
Contoh 3
Tentukan bayangan dari persamaan garis x – 2y – 3 = 0 pada pencerminan terhadap sumbu x!
Pembahasan:
Gunakan rumus pencerminan transformasi geometri (x,y) menjadi (x’, y’)
Dimana x’ = x dan x = x’
Y’ = -y dan y = -y’
Selanjutnya, subtitusikan x’ x= dan y’ = -y pada persamaan garis x – 2y – 3 = 0.
X – 2y – 3 = 0
(x’) – 2(-y’) – 3 = 0
Maka X’ + 2y’ -3 = 0
Jadi, bayangan dari persamaan garis x – 2y – 3 = 0 pada pencerminan terhadap sumbu x adalah x + 2y – 3 = 0.
Contoh 4
Apabila titik C(-2, 6) direfleksikan terhadap garis y = -x, berapakah koordinat bayangannya?
Pembahasan:
Dalam hal ini, gunakan rumus refleksi P(x, y) = P’(-y, -x).
C(x, y) = C’(-y, -x)
= C’(-6, -(-2)) = C’(-6, 2)
Jadi, bayangan titik C(-2, 6) oleh pencerminan berada di titik C’(-6, 2).
Contoh 5
Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah…..
Pembahasan:
Rumus dasar, yakni P (x,y) menjadi P’ (x’,y’)….. (1)
Jika pencerminan pada garis y=x, maka P (x,y) menjadi P’ (y,x)….. (2)
Berdasarkan rumus 1 dan 2, maka:
x’ = y dan y’ = x …. (3)
Lalu, subtitusikan rumus 3 ke garis y= 2x + 2
x’ = 2y + 2
2y = x’-2
y= x/2 – 1
Jadi, hasil pencerminannya adalah y= x/2 – 1.
Jenis-Jenis Transformasi Geometri
Selain mengetahui rumus pencerminan transformasi geometri, kamu juga bisa mengetahui apa saja jenis transformasi geometri untuk menambah pengetahuanmu. Berikut ini masing-masing penjelasannya:
1. Rotasi
Rotasi atau perputaran pada transformasi geometri merupakan pemindahan titik objek dengan cara memutar objek sejauh x derajat terhadap suatu titik tertentu. Pada bidang datar, ada beberapa hal yang menentukan sebuah rotasi, seperti titik pusat rotasi, besaran sudut, dan arah sudut rotasi.
Besaran sudut rotasi adalah sudut antara garis yang menghubungkan titik asal dan titik bayangan ke pusat rotasi. Sementara itu, apabila arah sudut rotasi searah dengan jarum jam, maka nilai sudut rotasi adalah negatif. Sedangkan pemutaran yang berlawanan arah jarum jam hasilnya positif.
2. Dilatasi
Jenis transformasi geometri selanjutnya yaitu dilatasi. Ini mencakup perubahan ukuran sebuah objek, dimana bentuk dan posisi awal dan akhir ukurannya akan berubah, meski tidak diputar. Perubahan jarak titik pada dilatasi menggunakan faktor pengali. Rumus umum untuk dilatasi adalah:
(x’, y’) = (k, k) (x-a, y-b) + (a, b) = (k(x – a) + a, k(y-b) + b)
Contoh sederhana dari dilatasi adalah ukuran ketika mencetak foto, misalnya ukuran 3 x 4 atau 4 x 6. Ukuran ini dapat kamu perbesar dan perkecil dengan skala tertentu tanpa memutarnya.
3. Translasi
Translasi merupakan perpindahan suatu titik sepanjang garis lurus, tanpa mengubah arah dan ukurannya. Rumus umum dalam translasi pada titik (x, y) yang berpindah sejauh vektor (a, b) adalah:
(x’, y’) = (x, y) + (a, b)
(x’, y’) = (x + a, y + b) dimana (x’, y’) adalah titik bayangan.
Contoh sederhana dari translasi dalam kehidupan sehari-hari bisa kamu lihat pada orang yang bermain perosotan. Orang ini dapat berpindah tempat dengan jarak tertentu, tanpa mengalami suatu perubahan apapun. Nyatanya, orang ini hanya berpindah posisi dari atas ke bawah, tanpa berubah postur atau ukurannya.
Baca Juga : Deret Geometri: Definisi, Rumus, Jenis, dan Contoh Soalnya
Sudah Paham Rumus Pencerminan Transformasi Geometri?
Secara keseluruhan, ada enam persamaan umum dalam refleksi, baik terhadap sumbu maupun garis. Persamaan tersebut adalah refleksi terhadap sumbu x dan sumbu y, refleksi terhadap garis y = x, garis y = -x, garis x = h, dan garis y = k. Lebih lanjut, kamu bisa memahami lebih dalam melalui contoh soal dan pembahasannya juga, lho.