Deret geometri adalah salah satu konsep penting dalam matematika yang melibatkan urutan bilangan dengan rasio tetap antara setiap pasangan bilangan. Dalam deret ini, setiap suku bilangan bisa Anda dapatkan dengan mengalikan suku sebelumnya dengan suatu bilangan tetap.
Memiliki pemahaman yang baik tentang deret ini sangat signifikan karena deret ini memiliki banyak penerapan yang luas dalam berbagai disiplin ilmu. Termasuk dalam bidang keuangan, fisika, dan ilmu komputer. Artikel ini akan membantu Anda memahami konsep deret geometri dengan lebih baik.
Pengertian Deret Geometri
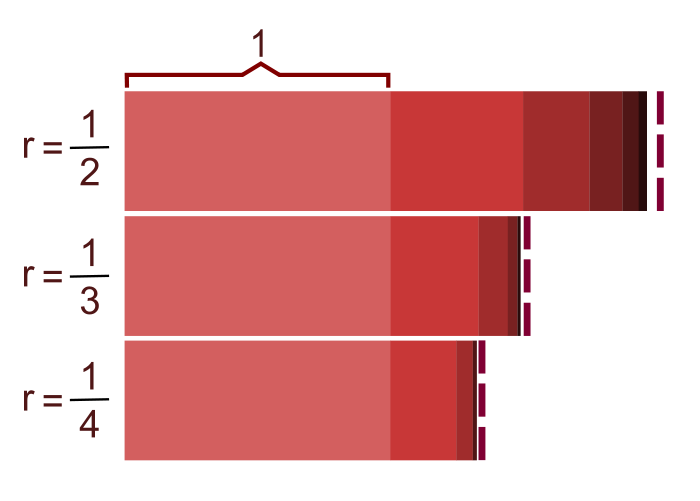
Deret geometri adalah rangkaian bilangan yang mana setiap bilangan berikutnya diperoleh dengan mengalikan bilangan sebelumnya dengan bilangan tetap yang disebut rasio. Perbedaan setiap pasangan bilangan dalam deret berturut-turut akan selalu konstan.
Dalam deret ini, suku pertama ditandai sebagai “a”, dan rasio umum antara setiap dua suku berturut-turut ditandai sebagai “r”. Dengan begitu, deret matematikanya akan berbentuk a, ar, ar² dan seterusnya. Rasio umum dapat berupa angka positif atau negatif, tergantung pada pola perkalian yang terjadi antara suku-suku.
Deret ini banyak berguna dalam berbagai bidang matematika dan ilmu pengetahuan, termasuk fisika, ekonomi, dan komputer sains. Mempelajari deret geometri dapat membantu Anda memahami pola-pola matematika yang muncul dalam berbagai konteks.
Contoh Deret Geometri

Beberapa contoh deret ini adalah sebagai berikut:
- 1/4, 1/8, …. adalah urutan geometris di mana a = 1/4 dan r = 1/2
- -4, 2, -1, 1/2, -1/4, … adalah urutan geometris di mana a = -4 dan r = -1/2
- π, 2π, 4π, 8π,…. adalah urutan geometris di mana a = π dan r = 2
- √2, -√2, √2, -√2, … adalah urutan geometris di mana a = √2 dan r = -1
Jenis Deret Geometri
Ada dua jenis urutan geometri berdasarkan jumlah istilah di dalamnya. Berikut ini penjelasannya:
1. Deret Geometri Terbatas
Urutan geometri terbatas adalah deret dengan jumlah suku yang terbatas atau terdefinisikan. Dalam urutan ini, suku-suku berikutnya dapat terhitung dengan mengalikan suku sebelumnya dengan rasio yang sama. Contohnya adalah urutan 2, 6, 18, 54, …. 13122, di mana suku terakhirnya adalah 13122.
2. Deret Geometri Tak terbatas
Sedangkan urutan geometri tak terbatas atau tak terhingga adalah deret matematika dengan jumlah suku yang tak terbatas atau tidak terdefinisikan. Dalam urutan ini, suku-suku berikutnya juga dihasilkan dengan mengalikan suku sebelumnya dengan rasio yang sama.
Deret tak terhingga adalah sebuah deret matematika yang memiliki sejumlah suku yang tak terhingga atau n = ∞. Secara teori, deret ini dapat terbagi menjadi dua jenis, yaitu deret tak terhingga yang konvergen dan deret tak terhingga yang divergen.
Deret tak terhingga konvergen adalah deret dengan nilai rasio (r) yang lebih besar dari -1 tapi kurang dari 1. Dalam deret ini, suku-suku deret akan semakin mendekati suatu nilai batas (limit) ketika jumlah suku yang diambil semakin banyak.
Contohnya adalah urutan 2, -4, 8, -16, … di mana tidak ada suku terakhir yang terdefinisikan. Dalam urutan tak terbatas, pola perkalian antara suku-suku dapat menghasilkan nilai yang semakin besar atau semakin kecil secara tak terhingga.
Rumus Deret Geometri
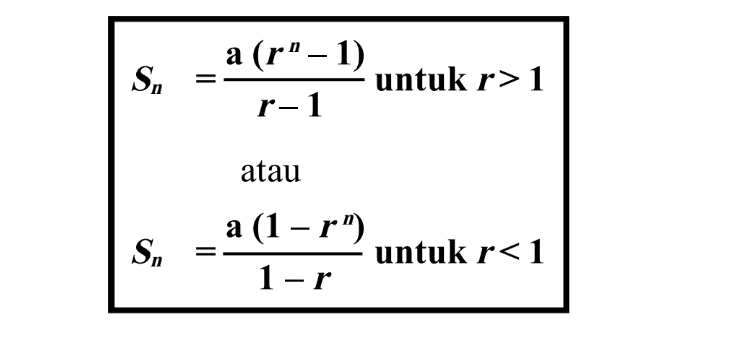
Berikut adalah daftar semua rumus deret geometri untuk setiap urutan geometris a, ar, ar², ar³, … arⁿ
- Istilah suku ke-n, aₙ = arⁿ ⁻ ¹ (atau) aₙ = r aₙ ₋ ₁
- Jumlah n suku pertama, Sₙ = a(rⁿ – 1)(r – 1) ketika ≠ 1 dan Sₙ = na ketika = 1.
- Jumlah suku tak terbatas, S∞ = a(1 – r) ketika |r| < 1 dan S∞ menyimpang ketika |r| ≥ 1.
Dalam barisan aritmatika, suku pertama memiliki simbol U1 atau a. Rasio atau selisih antara setiap dua suku berturut-turut memiliki simbol sebagai r. Jumlah suku dalam barisan akan bertanda “n”. Jumlah dari n suku pertama dalam barisan, simbolnya sebagai Sn.
Ada hubungan yang penting antara suku ke-n dalam barisan (Un) dan jumlah n suku pertama (Sn). Hubungan ini dapat dinyatakan sebagai Un = Sn – Sn-1. Artinya, suku ke-n akan diperoleh dengan mengurangi jumlah n suku pertama dari jumlah n-1 suku pertama.
Baca Juga : Contoh Barisan dan Deret Aritmatika, Rumus, dan Pembahasannya
Contoh Soal Deret Geometri dan Pembahasannya
Supaya pemahaman Anda terkait konsep deret matematika ini semakin mendalam, berikut adalah contoh soal beserta pembahasannya:
1. Contoh Soal 1
Cari persamaan untuk suku umum dari deret geometri yang diberikan dan gunakan untuk menghitung suku ke-10: 3, 6, 12, 24, 48…
Pembahasan:
Mulailah dengan mencari rasio umum
r = (6) / (3) = 2
Perhatikan bahwa rasio antara dua suku berturut-turut adalah 2. Deret tersebut memang merupakan suatu urutan geometri dengan suku pertama a1 = 3 dan rasio r = 2.
an = a1 x r(n-1)
Oleh karena itu, Anda dapat menulis suku umum an = 3 x 2(n-1) dan suku ke-10 dapat Anda hitung sebagai berikut:
a10 = 3 x 2(10-1) = 3 x 2(9) = 1.536
Jadi, persamaan untuk suku umum adalah an = 3 x 2(n-1) dan suku ke-10 adalah 1.536.
2. Contoh Soal 2
Temukan semua suku antara a1 = −5 dan a4 = −135 dari suatu deret geometri. Dengan kata lain, temukan semua rata-rata geometri antara suku pertama dan suku keempat!
Pembahasan:
Mulailah dengan mencari rasio umum r. Dalam kasus ini, Anda diberikan suku pertama dan suku keempat:
ana4 = a1/r^(n-1) : a1/r^3
Substitusikan a1 = −5 dan a4 = −135 ke dalam persamaan di atas, lalu selesaikan untuk r.
-135r3 = -5r3
Selanjutnya, gunakan suku pertama a1 = −5 dan rasio umum r = 3 untuk menemukan persamaan untuk suku ke-n dalam deret.
an = a1 x r(n-1)
an = -5 x 3(n-1)
Sekarang, Anda dapat menggunakan an = -5 x 3(n-1), di mana n adalah bilangan bulat positif, untuk menentukan suku-suku yang hilang.
a1 = -5 x 3(1-1) = -5 x 3(0) = -5
a2 = -5 x 3(2-1) = -5 x 3(1) = -15
Terakhir, a3 = -5 x 3(3-1) = -5 x 3(2) = -45
Jadi, suku-suku yang hilang adalah -15 dan -45.
3. Contoh Soal 3
Tentukan jumlah 18 suku pertama dari barisan geometri 2, 6, 18, 54, …..
Pembahasan:
Dalam kasus ini, suku pertama adalah a = 2.
Rasio umumnya, r = 6/2 = 18/6 = 54/18 = … = 3.
Jumlah suku adalah n = 18.
Rumus jumlah urutan geometri terbatas adalah,
Sₙ = a(rⁿ – 1)(r – 1)
S₁₈ = 2(3¹⁸ – 1) / (3 – 1) = 3¹⁸ – 1.
Jadi jumlah dari 18 suku pertama urutan geometri yang diberikan adalah 3¹⁸ – 1.
4. Contoh Soal 4
Tentukan jumlah suku-suku dari urutan geometri tak hingga berikut ini: 1/2, 1/4, 1/8… ∞
Pembahasan:
Dalam kasus ini, suku pertama adalah a = 1/2.
Rasio umumnya, r = (1/4) / (1/2) = (1/8) / (1/4) = … = 1/2.
Kita memiliki |r| = |1/2| = 1/2 < 1. Jadi, deret geometri ini konvergen.
Jadi, jumlah dari deret geometri tak hingga ini adalah:
S∞ = a(1 – r)
S∞ = (1/2)/(1 – 1/2) = (1/2) / (1/2) = 1.
Jadi jumlah dari deret geometri tak hingga yang diberikan adalah 1.
Sudah Paham dengan Konsep Deret Geometri?
Pada intinya, deret geometri menjadi salah satu konsep penting dalam matematika yang berguna untuk menggambarkan pola pertumbuhan suku-suku dalam suatu urutan. Dalam deret ini, setiap suku diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap yang menyebutnya rasio. Deret ini memiliki berbagai aplikasi dalam berbagai bidang, mulai dari ilmu pengetahuan alam hingga keuangan. Memahami dan menguasai konsep deret geometri dapat membantu Anda menganalisis pola dan memprediksi nilai-nilai di masa depan.

