Apakah kamu mengenai peluang kejadian bersyarat? Probabilitas bersyarat ini dapat membantu kamu dalam memprediksi kejadian di masa depan dengan tepat. Dengan begitu, kamu bisa menemukan keputusan yang tepat. Nah, artikel ini membahas pengertian, rumus, hingga contoh soalnya.
Apa Itu Peluang Kejadian Bersyarat?

Peluang atau probabilitas adalah cara mengungkapkan suatu peristiwa akan terjadi maupun sudah terjadi.
Dalam matematika peluang dinotasikan sebagai P(A). Maksudnya, P adalah peluang kejadian yang terjadi dari peristiwa A. Nilainya bisa saja 0 ataupun 1.
Peluang ini dibedakan menjadi 3 yaitu peluang kejadian bebas, majemuk, dan frekuensi harapan.
Peluang kejadian bebas yaitu dua kejadian yang saling bebas atau tidak memiliki kaitan. Sedangkan, peluang kejadian majemuk adalah dua kejadian yang bisa saling lepas atau memiliki kaitan seperti peluang kejadian bersyarat.
Peluang kejadian bersyarat adalah bentuk dari peluang kejadian majemuk dimana terdapat peristiwa A dan B.
Maksudnya, peristiwa A adalah penyebab terjadinya peristiwa B. Sehingga hal tersebut dinamakan peluang kejadian bersyarat.
Jika ditelaah lebih lanjut, banyak sekali peluang dari sebuah kejadian di dunia ini. Misalnya, terjadinya hujan. Kamu bisa memprediksinya lewat keadaan cuaca, angin, maupun melihat keadaan di pantai.
Rumus Peluang Kejadian Bersyarat
Berikut ini rumus dari peluang kejadian bersyarat yang perlu kamu pahami, yaitu:
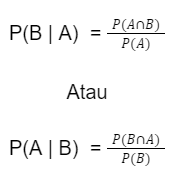
Dengan syarat P(A ) atau P(B) tidak boleh sama dengan 0.
Keterangan:
- P (B| A) = Peluang kejadian B dengan syarat A
- P (A ∩ B) = Peluang kejadian A irisan kejadian B
- P (A) = peluang kejadian A
- P (B) = peluang kejadian B
Baca Juga : Peluang Kejadian Majemuk: Pengertian, Jenis, Contoh Soal, dan Pembahasan
5 Manfaat Peluang Kejadian Bersyarat
Peluang bersyarat digunakan untuk berbagai bidang kehidupan antara lain sebagai berikut.
1. Meramalkan Cuaca
Cuaca yang berubah ubah pasti tidak bisa kamu tebak secara cuma-cuma. Dalam meramalkannya, pasti diperlukan data di masa lalu.
Nah, data tersebut digunakan sebagai data cuaca di masa depan. Kamu bisa melihatnya di ramalan cuaca per minggu di aplikasi cuaca.
2. Bidang Olahraga
Pada bidang olahraga, biasanya peluang bersyarat digunakan sebagai penentu hasil perlombaan. Mereka memakai banyaknya kemenangan yang pernah atlet capai.
3. Bidang Asuransi
Dalam bidang asuransi, biasanya peluang kejadian bersyarat digunakan sebagai pengambilan keputusan. Mereka akan memakai metode ini untuk mencairkan jaminannya.
4. Mitigasi Bencana
Hal ini serupa dengan meramalkan cuaca. Kamu perlu data di masa lalu untuk melakukan mitigasi bencana jika memakai metode peluang bersyarat.
Dengan begitu, kamu bisa mengetahui kapan terjadinya bencana. Misalkan seperti kapan terjadinya banjir, gunung meletus, abrasi, dan lainnya.
5. Permainan Kartu
Apakah kamu pernah menjumpai persoalan kejadian bersyarat dalam permainan kartu? Nah, dalam bermain kartu kamu bisa memprediksi kapan kamu akan memenangkan perlombaan. Dengan demikian, kamu bisa menanggulangi terjadinya salah mengambil kartu.
5 Contoh Soal Peluang Kejadian Bersyarat

1. Soal Pertama
Sebuah dadu akan kamu lempar sekali. Tentukan peluang munculnya mata dadu yang ganjil dengan syarat yaitu muncul kejadian mata dadu prima!
Jawab:
Misalnya, A adalah kejadian munculnya angka prima dengan penjelasan sebagai berikut :
Ruang sampel dari mata dadu: (S)= {1,2,3,4,5,6}, maka n(S)=6
Ruang sampel kejadian A untuk mata dadu prima: A = {2,3,5}, sehingga n(A)=3.
Untuk peluang kejadian A sebagai berikut, yaitu:
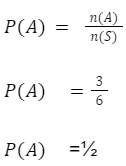
Setelah itu, mari kita hitung B. Misal B adalah kejadian dari munculnya mata dadu yang ganjil. Ruang sampel B = {1,3,5} sehingga n(A)=3.
Maka, peluang irisan dari peluang A dan B adalah P (A∩B) = {3,5}, dengan n(A∩B)=2. Peluang irisannya adalah sebagai berikut.
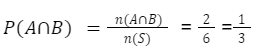
Kemudian, mari kita menentukan peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima P(B | A).
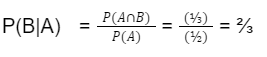
Jadi, hasil dari soal di atas adalah ⅔.
2. Soal Kedua
Sebuah kotak berisi bola merah dan bola putih. Berikut tabel dari penjelasan bola-bola yang ada dalam kotak, yaitu:
| Tanda | Hitam | Putih | Total |
| X | 5 | 3 | 8 |
| Y | 1 | 2 | 3 |
| Total | 6 | 5 | 11 |
Dari beberapa bola yang ada pada kotak tersebut, nantinya akan dipilih satu bola secara acak. Tentukan peluang dari kejadian terambil bola hitam bertanda X!
Jawab:
Pertama, tentukan peluang dari kejadian munculnya bola bertanda X sebagai berikut.
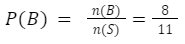
Ada 8 bola yang memiliki tanda X dan terdapat 5 bola berwarna hitam. Artinya, n(B∩X)=5
Peluang irisannya:
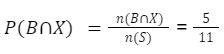
Setelah menghitung peluang irisan, mari kita cari peluang bersyarat pengambilan bola warna hitam (B) dengan syarat bertanda X .
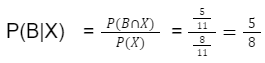
Jadi, peluang dari kejadian terambil bola hitam bertanda X adalah 58.
3. Soal Ketiga
Terdapat dua orang kakak beradik suka menonton film. Peluang kakak nonton film horor = 0,75. Sedangkan, peluang adik untuk menonton film horor sendiri adalah 0,60. Kemudian peluang kakak maupun adik menonton film horror adalah 0,60.
Tentukan peluang kakak nonton film horor jika adik telah menonton film horor itu terlebih dahulu.
Jawab:
- Peluang kakak nonton kartun sendiri, P(A)=0,75
- Peluang adik nonton kartun sendiri, P(B)=0,60
- Peluang kakak atau adik nonton kartun, P(AUB)=0,60
Pertama, kita cari P(A∩B) terlebih dahulu. Masih ingat bukan cara mencari irisan pada bab gabungan? Nah inilah rumusnya, yaitu:
P(A U B) = P(A) + P(B) – P(A ∩ B)
P(A U B) – P(A) – P(B)= – P(A ∩ B)
P(A) + P(B)-P(A U B) = P(A ∩ B)
Maka, substitusikan peluang pada penjelasan diatas ke dalam rumus tersebut.
P(A) + P(B)-P(A U B) = P(A ∩ B)
0.75 + 0.60 – 0.60= P(A ∩ B)
0.75 = P(A ∩ B)
Kemudian, hitung peluang kakak nonton film kartun jika adik telah nonton terlebih dahulu yang artinya dapat dikatakan peluang A dengan syarat B.
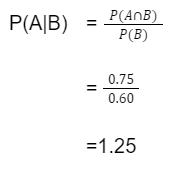
4. Soal Keempat
Seorang siswa mempunyai peluang untuk lulus dari ujian nasional matematika sebesar 0.65.
Sedangkan, ia harus menjalani ujian komputer setelah lulus ujian matematika dengan peluang sebesar 0.80. Maka, peluang siswa tersebut untuk lulus keduanya berapa?
Jawab:
Mari kita misalkan, P(M) adalah peluang matematika, dan P(K) adalah peluang ujian komputer. Maka, P(K|M) merupakan peluang lulus ujian komputer setelah lulus matematika. Dengan begitu, cara mencari peluangnya sebagai berikut.
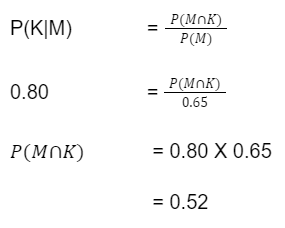
Jadi, peluang siswa tersebut untuk lulus kedua ujian tersebut sebesar 0.52
5. Soal Kelima
Di kota Surabaya, peluang untuk tiap hari cerah adalah 0.80. Diketahui bahwa peluang untuk suatu hari juga cerah dan berawan adalah 0.30. Maka, berapa peluang untuk hari ini berawan jika awalnya cerah?
Jawab:
Misalnya,
- Peluang untuk cerah , P(A)=0.80
- Peluang untuk cerah dan berawan, P(A ∩ B)=0.3
Maka, hasilnya sebagai berikut:

Jadi, peluang untuk berawan setelah cerah adalah 83 .
Kamu Siap Mengerjakan Soal Peluang Kejadian Bersyarat?
Semoga artikel ini dapat membantu kamu dalam memahami peluang kejadian bersyarat. Namun, 5 soal tersebut tentu belum cukup. Kamu perlu menambah wawasan dengan membaca literatur lain serta perbanyak latihan soal. Dengan demikian, kamu mampu mengerjakan soal dengan benar.

