Determinan merupakan salah satu konsep yang ada dalam ilmu Matematika dan berperan besar dalam kemajuan teknologi yang canggih hari ini. Tapi, apa sebenarnya determinan itu? Lalu, bagaimana fungsinya di dalam kehidupan sehari-hari? Yuk, gali informasinya secara mendalam bersama-sama lewat artikel ini!
Apa Itu Determinan?

Secara sederhana, determinan atau juga bisa disebut sebagai determinan matriks adalah nilai yang bisa kamu hitung dari unsur suatu matriks persegi. Konsep ini juga biasa dikenal dengan istilah faktor penentu, atau penentu.
Kalau kamu belajar matriks, kamu akan sadar, bahwa matriks persegi ini maksudnya adalah matriks yang tersusun atas kolom dan baris yang jumlahnya sama banyak. Misalnya saja, matriks 2 x 2 atau 3 x 3.
Sebagai salah satu cabang ilmu dari matematika, kamu bisa menganggapnya sebagai faktor penskalaan yang tergambar melalui matriks. Contohnya, faktor penentu dari matriks A bisa kamu tulis dengan tanda det A, det(A), atau |A|.
Lalu, bagaimana kalau jumlah kolom dan barisnya beda? Tentu konsep tersebut tidak akan bekerja.
Fungsi/Manfaat Belajar Determinan
Pelajaran tentang faktor penentu di bangku sekolah mungkin terlihat tidak menarik, cenderung sulit dan tidak aplikatif dalam kehidupan nyata.
Padahal, kalau kamu memahami konsepnya dengan benar, kamu akan tahu kalau manfaat belajar determinan sangatlah besar di dalam kehidupan sehari-hari. Kamu dapat merasakan manfaat konsep matematika ini jika sedang menghadapi masalah yang berkaitan dengan angka dan data.
Apa saja masalah yang bisa dipecahkan oleh salah satu konsep matematika ini? Sedikitnya, ada enam masalah yang bisa kamu selesaikan menggunakan konsep faktor penentu, seperti yang disebutkan di bawah ini.
1. Menganalisis input ataupun output di dalam bidang ekonomi, pendidikan, statistik, kimia, manajemen, dan bidang teknologi.
2. Memudahkan kamu dalam menganalisis masalah ekonomi yang terdiri dari berbagai variabel.
3. Memudahkan kamu dalam memecahkan operasi penyelidikan, contohnya untuk mengetahui sumber lokasi minyak bumi.
4. Salah satu konsep yang ada di matematika ini sangat berguna dalam penerapan bidang keamanan komputer dan pemrograman yang sama-sama membutuhkan array.
5. Melakukan enkripsi data di dalam ilmu komputer.
6. Berperan besar dalam menciptakan sebuah algoritma di berbagai bidang teknologi dan informasi.
Tidak berhenti sampai di situ saja, konsep determinan turut berperan besar dalam performa ponsel pintar atau laptop yang selama ini kamu gunakan untuk mencari informasi, hingga kamu bisa membaca artikel ini.
Bagaimana Cara Mencari Faktor Penentu lewat Hitungan Matematis?
Sekarang, kamu akan mempelajari bagaimana caranya mencari determinan matriks, baik itu di dalam matriks 2 x 2 ataupun 3 x 3. Yuk, kamu pelajari bersama!
Cara Mencari Determinan Matriks (2 x 2)
Berikut adalah cara yang bisa kamu lakukan untuk mencari determinan 2 x 2.
Matriks 2 x 2 terdiri dari dua kolom dan dua baris. Misalnya, kamu memiliki matriks X yang terdiri dari (a), (b), (c), dan (d). Nah, bentuk matriksnya akan seperti ini:
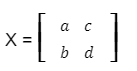
Kamu bisa menuliskan faktor penentu matriks X dalam bentuk det X = |X|.
Nah, ini adalah cara yang bisa kamu lakukan dalam menghitungnya:
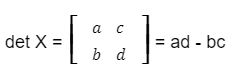
Dengan begitu, rumusnya adalah
|X| = ad – bc
Kira-kira itulah rumus yang bisa kamu pakai untuk menghitung faktor penentu matriks 2 x 2.
Cara Mencari Determinan Matriks (3 x 3)
Lalu, kalau kamu melihat formula 3 x 3, bagaimana cara menghitungnya? Ada dua cara yang bisa kamu lakukan dalam menghitung faktor penentu matriks 3 x 3, yaitu dengan cara Sarrus dan cara minor kofaktor. Simak pembahasan kedua cara tersebut dalam uraian berikut, yuk!
1. Cara Sarrus
Anggaplah kamu punya matriks X sebagai berikut:
X =

Cara menghitung determinan matriks dengan metode sarrus adalah dengan mengikuti langkah-langkah di bawah ini.
- Susun ulang matriks dengan penambahan 2 baris dan 3 kolom.
- Lalu, kamu bisa membuat garis diagonal ke kanan (warna merah) dengan operasi penjumlahan dan diagonal ke kiri (warna hijau) dengan operasional pengurangan.
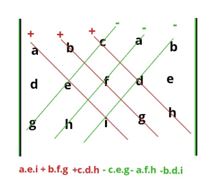
Rumus hitung determinan matriks menggunakan metode Sarrus adalah:
|X| = (a .e .i) + (b.f.g) + (c.d.h) – (c.e.g) – (a..f.h) – (b.d.i)
Lalu, bagaimana cara menghitung salah satu konsep faktor penentu ini menggunakan rumus minor kofaktor?
2. Cara Minor Kofaktor
Kamu bisa beranggapan bahwa kamu masih punya matriks 3 x 3 yang sama, matriks (X),
X =

Ada tiga langkah utama yang harus kamu lakukan dalam menggunakan rumus ini:
- cari minornya terlebih dahulu (M11, M12, M13),
- kemudian cari kofaktornya (C11, C12, C13), lalu
- masukkan ke dalam rumus determinan.
Mula-mula, kamu cari minor dahulu. Bagaimana caranya? Misalnya, kamu ingin mencari A11. Coba perhatikan matriks (X) ini

Karena kamu mencari minor A11, hapus baris pertama (a, b, c) dan kolom pertama (a, d, g). Setelah dihapus, kamu akan memperoleh sisanya.
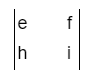
Cara ini pun juga berlaku untuk mencari minor yang lain, seperti M12 dan M13. Kamu tinggal gunakan konsep mencari faktor penentu matriks 2 x 2, dan kamu akan menemukan hasilnya.
Lalu, bagaimana caranya mencari kofaktor?
Ini dia rumus untuk mencari kofaktor:
Cij = -1i+j |Mij|
Contohnya, kamu ingin mencari C11. Berarti, i = 1, j = 1
C11 = -11+1 |M11|
Maka, perhitungan untuk mencari C11 adalah
C11 = -11+1 |e.i – f.h|
Perhitungan ini pun juga berlaku jika kamu mencari C12 dan C13.
Nah, setelah kamu sudah punya minor dan kofaktor, sekarang saatnya kamu bisa mencari faktor penentunya. Rumus untuk mencari determinan dari cara ini adalah sebagai berikut:
|X| = X11.C11 + X12.C12 + X13.C13
Coba kamu perhatikan lagi matriks (X) yang sudah kamu punya
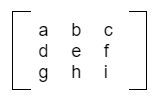
Dari sini, kamu bisa tahu kalau X11 = a, X12 = b, X13 = c. Maka, rumus ini juga bisa ditulis sebagai berikut:
|X| = a.C11 + b.C12 + c.C13
Menurut kamu, rumus mana yang lebih mudah? Rumus Sarrus atau rumus minor kofaktor?
Hafalkan Sifat Matriks Ini!
Sebelum kamu masuk ke contoh soal, kamu perlu tahu beberapa sifat yang berlaku di matriks dahulu.
Misalnya, ada matriks (A) dan (B), sifat-sifat matriksnya adalah sebagai berikut:
- |AB| = |A| |B|.
- |AT| = A, T adalah transpose matriks.
- |kA| = kn|A|, k = bilangan riil, n = ordo matriks A.
- |A-1| = 1/|A| (invers matriks).
- Determinan matriks akan bernilai 0 jika semua elemen pada baris dan kolomnya bernilai nol.
- Jika ada dua baris atau kolom yang elemennya sama atau kelipatannya, maka faktor penentu matriksnya bernilai nol.
Contoh Soal Determinan Matriks
Contoh soal yang akan tampil bertujuan untuk meningkatkan pemahamanmu tentang faktor penentu matriks.
Soal
Tentukan determinan dari matriks A di bawah ini dengan metode Sarrus!

Pembahasan
|A| = (a .e .i) + (b.f.g) + (c.d.h) – (c.e.g) – (a..f.h) – (b.d.i)
|A| = (4.5.0) + (-1.3.-2) + (1.4.0) – (1.5.-2) – (4.3.0) – (-1.4.0)
Jadi, |A| = 0 + 6 + 0 – (-10) – 0 – 0
|A| = 6 + 10 = 16
Baca Juga : Transpose Matriks: Pengertian, Ciri, Jenis, dan Contoh Soal
Yuk, Belajar Determinan Matriks!
Faktor penentu matriks bisa dibilang sebagai salah satu konsep di matematika yang sering menjadi momok bagi siswa karena tergolong sulit untuk dipahami. Namun, jika dipelajari secara tekun dan kamu mencoba untuk paham secara perlahan, kamu pasti akan mampu menguasai materi satu ini.Jika kamu suatu saat ingin fokus di bidang seperti komputer dan informatika, materi determinan matriks harus kamu kuasai betul-betul. Pasalnya, materi ini sangat aplikatif dengan bidang teknologi dan informasi.

