Dalam ilmu matematika, transpose matriks merupakan salah satu operasi matriks yang cukup populer. Sebab, konsep dasarnya cukup penting dalam analisis data, aljabar linear, dan berbagai bidang lainnya.
Untuk lebih jelasnya, artikel ini akan memberikan penjelasan singkat namun pada terkait transpose matriks, mulai dari pengertian, ciri-ciri, jenis, contoh soal sederhana hingga pembahasannya. Baca sampai selesai, ya!
Pengertian Transpose Matriks
Seperti pada penjelasan awal, teori ini melibatkan operasi matriks yang merupakan susunan beberapa bilangan dalam baris dan kolom. Nah, transpose matriks adalah satu operasi matematika yang diperoleh dengan menukar kolom dan baris dari suatu matriks.
Sederhananya, kolom matriks asal akan berubah menjadi baris ketika di transpose, dan baris matriks asal akan berubah menjadi kolom. Misalnya, jika kamu memiliki matriks A dengan dimensi m x n, maka hasil dari operasi transpose matriks A adalah matriks B dengan dimensi n x m.
Operasi ini umumnya berguna dalam berbagai konteks seperti pada ilmu matematika, ilmu komputer, fisika, dan bidang lain yang membutuhkan perhitungan matematis. Melalui operasi ini, kamu bisa mengubah susunan data dalam matriks untuk keperluan hitungan atau analisis.
Ciri-ciri Transpose Matriks
Operasi matematika ini memiliki beberapa ciri yang membedakannya dari matriks biasa. Berikut ini adalah beberapa ciri yang bisa membantu kamu dalam mengenali operasi transpose dalam ilmu matematika dan ilmu komputer:
1. Perubahan Baris dan Kolom
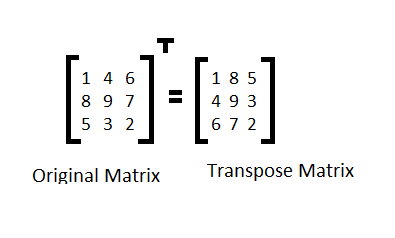
Hal paling mendasar yang membedakan operasi ini dengan matriks biasa adalah adanya perubahan pada bagian baris dan kolom. Dalam operasinya, proses ini melibatkan pertukaran posisi antara baris dan kolom dari matriks asal.
Dengan kata lain, elemen-elemen yang ada pada baris a akan berpindah dalam kolom b, dan kolom b akan berpindah ke baris a. Inilah esensi dari perubahan baris dan kolom yang menghasilkan struktur matriks baru yang memiliki orientasi yang berlawanan dengan matriks asal.
2. Penggunaan Notasi
Ciri selanjutnya adalah terkait dengan penggunaan notasi. Notasi dalam operasi transpose matriks akan menggunakan simbol tambahan untuk menunjukkan adanya perbedaan dengan matriks biasa.
Pada matriks biasa, notasi yang digunakan adalah berupa huruf kapital seperti A, B, C, dan seterusnya. Sedangkan notasi yang digunakan pada matriks transpose adalah dengan menambahkan simbol transpose (T) pada matriks asal.
Misalnya, jika matriks asal adalah A, maka operasinya akan ditulis sebagai Aᵀ. Simbol T ini menunjukkan bahwa matriks awal telah diubah menjadi matriks baru, yakni Aᵀ.
3. Perubahan Ordo
Dengan adanya perubahan baris dan kolom, jumlah ordo atau dimensi pada setiap garis dan kolom juga ikut berubah. Ordo dari operasi ini adalah kebalikan dari ordo matriks asli.
Contohnya, jika matriks A memiliki ordo 3×2, maka itu artinya matriks A memiliki 3 baris dan 2 kolom. Nah, jika di transpose, maka matriks A akan menjadi matriks baru yakni Aᵀ dan memiliki ordo 2×3 yang mana matriks Aᵀ memiliki 2 baris dan 3 kolom.
Jenis Transpose Matriks

Operasi transpose sendiri dapat dibedakan menjadi dua jenis. Biasanya, hal ini tergantung pada kebutuhan dari suatu perhitungan yang mengharuskan adanya transpose biasa dan transpose konjugasi. Berikut ini adalah sedikit penjelasan dari kedua jenis tersebut:
1. Transpose Matriks Biasa
Transpose pada matriks biasa merupakan operasi transpose dari sebuah matriks tanpa mengubah isi dari elemen-elemen matriks. Operasi pada matriks biasa hanya mengubah tata letak dari elemen baris menjadi kolom dan begitu juga sebaliknya.
Sebagai contoh, jika matriks A mempunyai ordo a x b, maka transpose akan mengubah tata letak dari baris dan kolom tersebut menjadi ordo b x a. Elemen a dan b tidak mengalami perubahan baik itu nilai maupun konjugasinya.
2. Conjugate Transpose
Conjugate transpose (transpose konjugasi) atau yang biasa dikenal sebagai transpose Hermitian adalah transpose matriks dengan menggabungkan dua operasi. Jenis ini biasa digunakan dalam ilmu mekanika kuantum, aljabar linear, dan beberapa bidang lain.
Operasi pertama adalah dengan melakukan transpose seperti biasa, dan operasi kedua adalah mengkonjugasikan semua elemen pada matriks tersebut. Contoh sederhana dari conjugate transpose adalah sebagai berikut:
A = | 1+2i 3-4i |
| 5+6i 7-8i |
Elemen baris pertama pada matriks A adalah 1+2i dan 3-4i dan elemen pada baris kedua yakni 5+6i dan 7-8i. Elemen pada kolom pertama adalah 1+2i dan 5+6i dan elemen pada kolom kedua yakni 3-4i dan 7-8i.
Nah, setelah dilakukan operasi konjugasi, hasilnya adalah sebagai berikut:
A* = | 1-2i 5-6i |
| 3+4i 7+8i |
Berdasarkan hasil konjugasi di atas, elemen pada baris pertama menjadi 1-2i dan 5-6i. Sedangkan elemen pada baris kedua adalah 3+4i dan 7+8i. Operasi matriks yang awalnya adalah pengurangan berubah menjadi penjumlahan, begitu pula sebaliknya.
Baca Juga : Matriks Identitas: Pengertian, Konsep, Sifat, dan Contoh Soal
Contoh Soal Transpose Matriks dan Pembahasannya
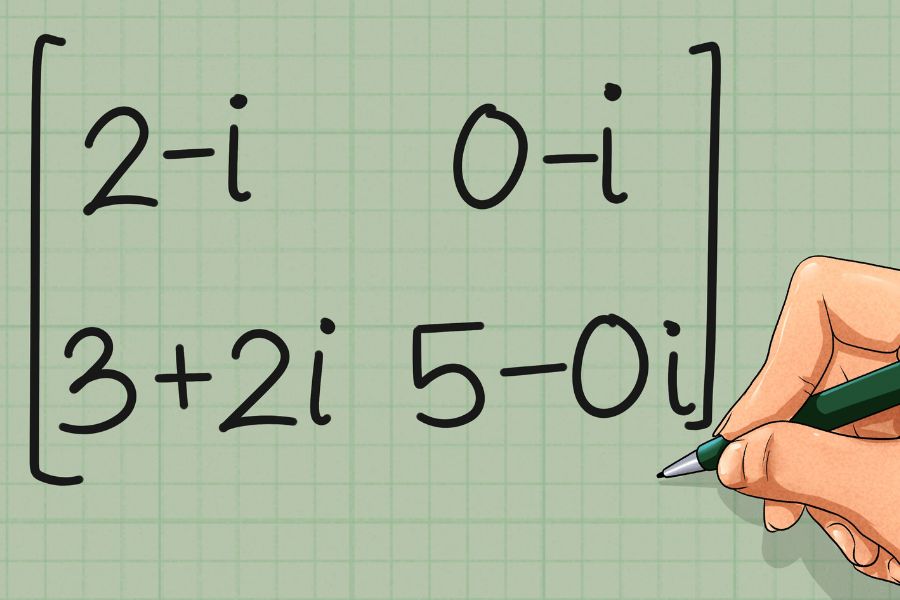
Berikut ini adalah contoh soal dan pembahasan lengkap yang akan membantu kamu dalam memahami konsep transpose matriks dengan lebih baik:
1. Contoh Soal Matriks Ordo 2×3
Ubahlah matriks berikut dengan melakukan transpose dan tuliskan hasilnya!
A = | 1 2 3 |
| 4 5 6 |
Pembahasan:
Matriks A memiliki beberapa elemen dengan susunan sebagai berikut:
- Baris pertama: 1, 2, 3
- Baris kedua: 4, 5, 6
- Kolom pertama 1, 4
- Kolom kedua: 2, 5
- Kolom ketiga: 3, 6
Langkah pertama yang harus kamu lakukan adalah dengan menukarkan posisi antara baris dan kolom dari matriks asal, yakni matriks A. Nantinya, hasil transpose dari matriks A (Aᵀ) adalah sebagai berikut:
Aᵀ = | 1 4 |
| 2 5 |
| 3 6 |
Transpose matriks dilakukan dengan cara menukarkan posisi baris dan kolom. Maka susunan dari matriks transpose Aᵀ adalah sebagai berikut:
- Baris pertama: 1, 4
- Baris kedua: 2, 5
- Baris ketiga: 3, 6
- Kolom pertama: 1, 2, 3
- Kolom kedua: 4, 5, 6
2. Contoh Soal Matriks Ordo 3×3
Ubahlah matriks berikut dengan melakukan transpose dan tuliskan hasilnya!
A = | 1 -2 3 |
| 4 -5 6 |
| 7 -8 9 |
Pembahasan:
Matriks A memiliki 3 baris dan 3 kolom elemen penyusun sebagai berikut:
- Baris pertama: 1, -2, 3
- Baris kedua: 4, -5, 6
- Baris ketiga: 7, -8, 9
- Kolom pertama: 1, 4, 7
- Kolom kedua: -2, -5, -8
- Kolom ketiga: 3, 6, 9
Setelah dilakukan transpose dengan cara menukarkan posisi baris dan kolom, maka susunan dari matriks baru yakni matriks Aᵀ adalah sebagai berikut:
Aᵀ = | 1 4 7 |
| -2 -5 -8 |
| 3 6 9 |
Maka, elemen penyusun dari 3 ordo matriks Aᵀ adalah sebagai berikut:
- Baris pertama: 1, 4, 7
- Baris kedua: -2, -5, -8
- Baris ketiga: 3, 6, 9
- Kolom pertama: 1, -2, 3
- Kolom kedua: 4, -5, 6
- Kolom ketiga: 7, -8, 9
Konsep Transpose Matriks Itu Mudah, Bukan?
Itulah pembahasan singkat terkait transpose matriks yang perlu kamu pahami, mulai dari pengertian, ciri-ciri, jenis, hingga contoh soal lengkap dengan pembahasannya. Pada dasarnya, operasi ini hanya mengubah tata letak baris dan kolom matriks asli, di mana menjadikan baris matriks menjadi kolom begitu juga sebaliknya.Pahami kasus khusus, seperti matriks simetri, di mana matriks adalah sama dengan transpose-nya sendiri. Dengan begitu, kamu akan tahu bagaimana transpose matriks berguna dalam menghubungkan konsep dengan berbagai bidang, seperti analisis data, pemrosesan gambar, atau pemrograman. Selamat belajar!

