Matriks Identitas: Pengertian, Konsep, Sifat, dan Contoh Soal

Matriks merupakan salah satu cara untuk menyelesaikan konsep matematika yang memiliki banyak variabel. Dengan pola struktur angka nol dan satu yang ditutup dengan tanda kurung, ini merupakan matriks identitas yang sangat mudah dikenali.

Oleh sebab itu, pola matriks dengan berbagai bentuk dan jenisnya sangat memudahkan seorang ekonomi dalam mengolah data. Begitu juga dengan seorang programmer dalam mengoperasikan kecerdasan buatan (AI). Seperti apa sih teorinya hingga bisa bermanfaat di segala bidang? Simak melalui artikel ini, yuk!

Apa Itu Matriks Identitas?

Sebagai dasar pemahaman Anda, matriks adalah suatu pola bilangan yang diisi dalam bentuk baris dan kolom dalam bentuk segi empat siku-siku. Bilangan tersebut merupakan penyusun matriks yang biasa dikenal sebagai entri dalam matriks.

Nah, matriks identitas atau matriks satuan merupakan suatu konsep matematika yang tergolong materi aljabar linier. Hitungan matriks ini merupakan salah satu dari beragam jenis matriks dalam ilmu matematika.  

Ciri khas matriks adalah pola bilangan nol dan satu yang tersusun membentuk persegi atau persegi panjang. Selain itu, terdapat dua kurung siku yang mengelilingi angka-angka tersebut.

Pada umumnya, untuk mengenali suatu bilangan matriks, Anda dapat menggunakan elemen atau entri dengan simbol huruf kecil. Sementara matriks sendiri menggunakan simbol huruf besar.

Pola susunannya terdiri dari baris dan kolom yang dapat menyatakan ukuran matriks dengan sebutan ordo. Baris merupakan jajaran angka yang membentang ke samping (horizontal), sedangkan kolom merupakan susunan angka dalam bentuk vertikal.

Sebelum itu, ketahui dulu bentuk umum dari matriks dalam ilmu matematika ini. berikut contohnya:

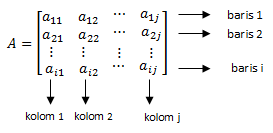
Walaupun terkesan rumit, karena susunan angka dan huruf tergabung menjadi satu, ternyata tidak serumit itu. Anda hanya perlu mengetahui arti dari beberapa huruf di atas beserta simboliknya. Berikut keterangannya:

• A : Simbol matriks dengan huruf besar
• i : banyaknya baris (horizontal)
• j : jumlah kolom (vertikal)
• i x j : ordo matriks

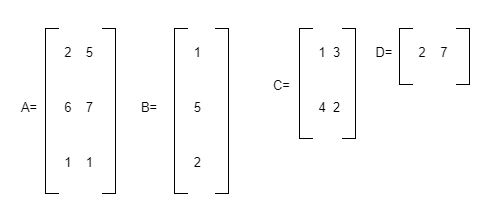
Ilustrasi di atas hanyalah contoh gambaran pola matriks. Matriks A menggunakan ordo 3×2, kemudian matriks B menggunakan ukuran 3×1, sedangkan matriks C berpola 2×2, dan matriks D menggunakan ordo 1×2. Penulisan ordo ini selalu diawali dengan jumlah baris, kemudian diikuti dengan jumlah kolom.

Konsep Matriks Identitas

Biasanya, matriks identitas menggunakan pola diagonal dengan elemen-elemennya memiliki angka satu, sedangkan yang lainnya adalah nol. Diagonal utama dalam suatu matriks merupakan susunan elemen yang membentuk garis miring dari pojok kiri atas ke pojok kanan bawah.

Sebenarnya, pola susunan seperti itu juga disebut sebagai matriks diagonal. Banyaknya jenis-jenis matriks ini tergantung dengan ukuran ordonya. Sebelum itu, yuk lihat dulu contoh-contoh susunan serta pola dari matriks identitas ini.

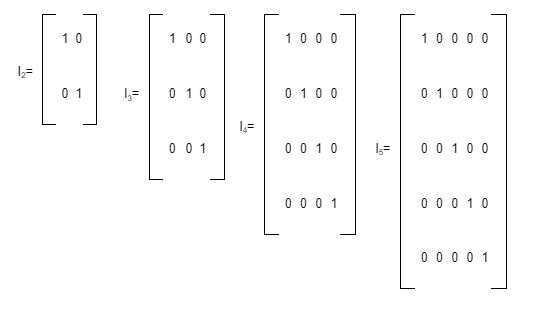
Dari susunan matriks di atas, terlihat bahwa matriks satuan memiliki ordo yang sama. Pada fungsi I₂ memiliki ordo 2×2, I₃ mengikuti pola 3×3, I₄ menggunakan pola 4×4, serta I₅ berordo 5×5.

Bagaimana Sifat Matriks Identitas?

Dari beberapa penjabaran definisi terkait matriks, pastinya Anda sudah tahu ciri utama dan yang paling mendasar. Selain susunan bilangan dan pola bentuknya, kira-kira apa saja sifat yang mewarnai matriks dengan dominan angka nol dan satu ini? Berikut uraiannya:

1. Berbentuk Persegi

Matriks identitas selalu memiliki pola bentuk persegi atau bujur sangkar, sehingga matriks ini terkenal dengan satuan yang selalu memiliki ordo sama, yaitu n x n. Seperti pada contoh di atas, jumlah baris dan kolom mulai dari I₂ sampai I₅ adalah sama.

2. Hasil Operasi Perkalian Matriks Identitas Adalah Tetap

Jika mengalikan matriks satuan dengan matriks apapun, maka hasilnya adalah matriks satuan. Akan tetapi, operasi perkalian tersebut dapat berlangsung apabila memenuhi beberapa kriteria berikut ini:

• Apabila matriks satuan merupakan faktor pengali pertama, maka matriks lainnya harus memiliki jumlah kolom sesuai dengan baris pada matriks satuan. Perhatikan contoh berikut:

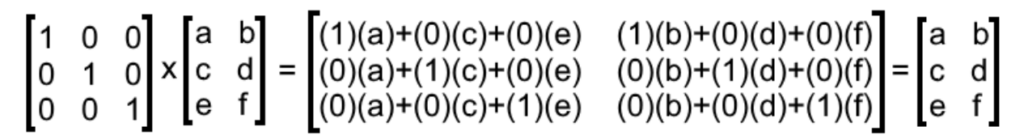
• Sementara itu, jika matriks satuan adalah pengali kedua, maka matriks lainnya harus memuat jumlah baris sesuai dengan kolom matriks satuan. Berikut ilustrasinya:

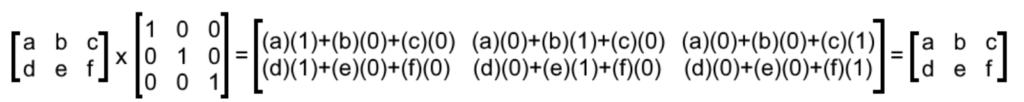
Dari dua aturan tersebut membuktikan bahwa sifat matriks satuan yang kedua adalah benar. Oleh sebab itu, nilai matrik dapat diformulasikan sebagai berikut:

I_m x A_mxn = A_mxn atau A_mxn x I_m =  A_mxn

Persamaan di atas ekuivalen dengan perkalian angka satu. Berapa pun bilangannya jika pengalinya adalah angka satu, maka hasilnya tetap bilangan tersebut. Oleh karena itu, matriks identitas ini disebut sebagai matriks satuan.

 3. Perkalian Dua Matriks Invers Menghasilkan Matriks Identitas

Apabila Anda mengalikan matriks dengan inversnya, maka Anda akan menghasilkan matriks satuan yang ordonya sama dengan matriks yang dikalikan. Secara matematis, berikut contohnya:

A x A^-1 = I = A^-1 x A

Dalam konteks ini, invers matriks memiliki peran penting dalam menyelesaikan sistem persamaan linear. Bahkan juga bermanfaat dalam pemecahan berbagai masalah matematika dan teknik yang melibatkan matriks. 

4. Penjumlahan Bilangan Matriks Identitas Sama dengan ‘n’

Seperti yang Anda tahu, matriks satuan memiliki karakteristik berpola diagonal dengan susunan angka satu dan nol. Sehingga, ketika Anda menjumlahkan seluruh angka yang ada di dalamnya, maka hasilnya adalah sesuai dengan ordo matriks tersebut.

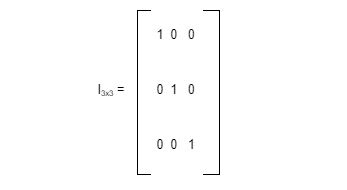
Persamaan matriks tersebut menunjukkan ordo 3×3 sehingga jika bilangan pada elemen-elemen matriks dijumlahkan hasilnya adalah 3. Pernyataan tersebut telah sesuai dengan sifat matriks satuan pada poin empat.

Baca Juga : Definisi Himpunan, Cara Menyatakan, Jenis, dan Contoh Soalnya

Contoh Soal Matriks Identitas

Setelah memahami sifat-sifat matriks satuan, coba Anda berlatih dalam menentukan suatu matriks berikut ini.

1. Contoh Soal 1

Tentukanlah apakah persamaan berikut ini merupakan suatu matriks identitas atau bukan.

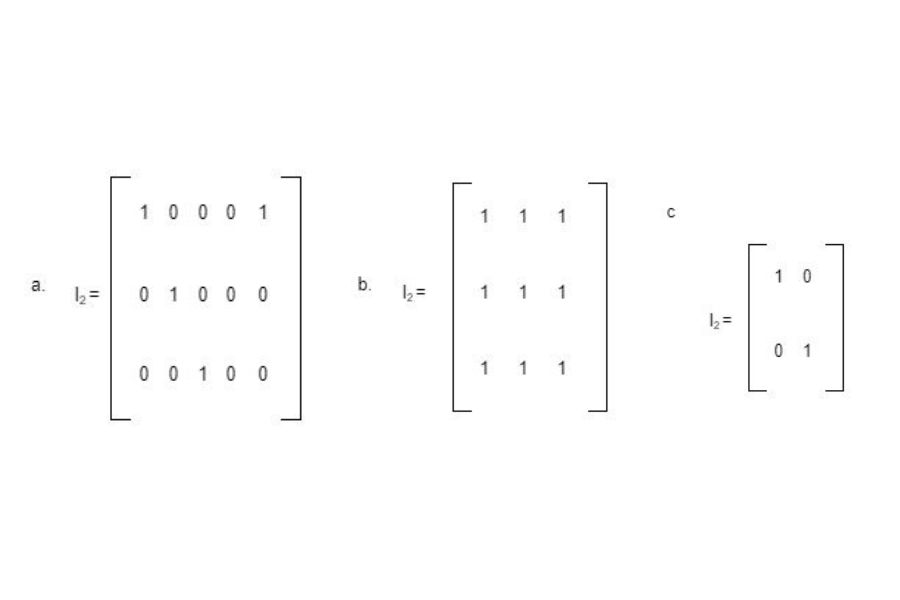
Penyelesaian:

1. Persamaan I₂ bukan termasuk dalam matriks satuan, sebab matriks tersebut memiliki ordo 4×3. Kondisi tersebut tidak sesuai dengan sifat-sifat matriks satuan.
2. Matriks I₃ juga tidak memuat definisi dan sifat matriks satuan. Sebab, elemen yang terkandung dalam matriks satuan adalah nol dan satu.
3. Sementara untuk persamaan I₄ merupakan matriks identitas, karena memenuhi syarat dan sifat dalam matriks satuan.

2. Contoh Soal 2

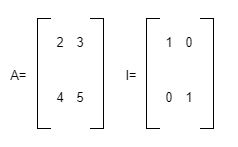
Jika diketahui persamaan matriks di atas, tentukanlah:

1. A x I
2. I x A
3. I x I

Penyelesaian:

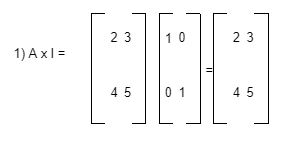
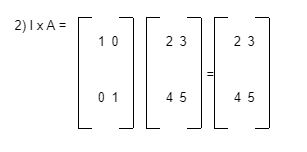
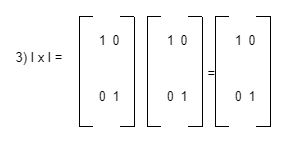
Sudah Tahu Fungsi Matriks Identitas dalam Kehidupan?

Sampai di sini apakah Anda sudah memahami bahkan mampu memetakan fungsi matriks identitas dalam kehidupan? Memang, dari gambaran soal dan persamaan terlihat sangat matematis yang mungkin Anda tidak menyadari bahwa beberapa kegiatan sehari-hari juga membutuhkan perhitungan matriks.

Salah satu contohnya adalah ketika Anda sedang makan bersama teman-teman, kemudian Anda yang memesan semua makanan teman Anda dan membayarnya. Nah, ketika Anda melakukan split bill itulah sebenarnya bisa menggunakan operasi perhitungan matriks.

Selain itu, Anda juga bisa menemukan penerapan konsep matriks dalam bidang statistika, ekonomi, ilmu komputer, bahkan untuk menentukan jadwal siaran televisi.Dengan begitu, Anda sudah tahu bagaimana perhitungan dan konsep dari matriks identitas. Tentunya Anda juga mendapatkan wawasan baru mengenai fungsi dari ilmu matematika statistik ini.