Apabila mendengar kata rotasi, pasti kita tidak asing lagi dengan artinya yakni berputar, seperti halnya perputaran planet yang mengelilingi matahari pada orbitnya masing-masing. Untuk pemahaman lebih lanjut, kamu dapat menyimak penjabaran secara singkat mengenai dinamika rotasi pada paragraf di bawah ini.
Pengertian
Dinamika rotasi adalah cabang ilmu fisika yang mempelajari gerakan rotasi suatu benda yang berputar di sekitar sumbu tertentu. Dalam dinamika rotasi, fokus utama adalah pada analisis gaya, momen inersia, percepatan sudut, dan hubungan antara gerakan rotasi dengan gaya-gaya yang menyebabkannya.
Besarannya
Terdapat beberapa besaran penting dalam dinamika rotasi yang menggambarkan gerakan rotasi suatu benda. Berikut adalah beberapa besaran tersebut:
1. Torsi (Momen Gaya)
Torsi (torque) adalah gaya yang menyebabkan rotasi suatu benda di sekitar sumbu tertentu. Ketika gaya torsi bekerja pada benda yang dapat berputar, benda tersebut akan mengalami perubahan kecepatan sudut.
Torsi mirip dengan gaya dalam gerakan translasi (gerakan linier), tetapi torsi bekerja pada benda yang berputar dan menyebabkan perubahan kecepatan sudut, sedangkan gaya dalam gerakan translasi menyebabkan perubahan kecepatan linear.
Torsi dapat didefinisikan sebagai hasil perkalian antara gaya (F) yang bekerja pada benda dan jarak tegak lurus (R) dari sumbu rotasi ke garis aksi gaya tersebut. Dalam rotasi matematis, torsi () dinyatakan sebagai:

Torsi memiliki arah rotasi tertentu yang sejalan dengan arah gaya dan sumbu rotasi. Untuk menghasilkan rotasi searah jarum jam, torsi harus memiliki arah yang keluar dari bidang gambar. Sedangkan untuk rotasi berlawanan arah jarum jam, torsi harus memiliki arah masuk ke dalam bidang gambar.
2. Inersia (Momen Inersia)
Momen inersia adalah suatu besaran fisika yang mengukur sejauh mana suatu benda menahan perubahan kecepatan sudutnya ketika dikenai torsi. Momen inersia sangat mirip dengan konsep massa dalam dinamika translasi.
Jika massa mengukur ketahanan suatu benda terhadap perubahan kecepatan translasional, maka momen inersia mengukur ketahanan suatu benda terhadap perubahan kecepatan rotasional.
Momen inersia bergantung pada distribusi massa benda terhadap sumbu rotasinya. Benda dengan momen inersia yang lebih besar akan membutuhkan torsi yang lebih besar untuk mencapai percepatan sudut tertentu dibandingkan dengan benda dengan momen inersia yang lebih kecil.
Momen inersia dapat dihitung menggunakan rumus berikut:
I=mr2
di mana:
I = momen inersia (kgm²)
m = massa partikel (kg)
r = jarak partikel ke sumbu (m)
3. Momentum Sudut
Momentum sudut (angular momentum) adalah kuantitas fisik yang menggambarkan seberapa besar benda berputar atau memiliki gerakan rotasi. Momentum sudut didefinisikan sebagai perkalian momen inersia suatu benda dengan kecepatan sudutnya. Secara sistematis, momentum sudut (L) didefinisikan sebagai:
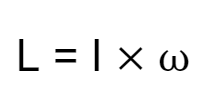
di mana:

Benda dengan momen inersia yang lebih besar akan memiliki momentum sudut yang lebih besar untuk kecepatan sudut yang sama.
Kecepatan sudut () adalah ukuran seberapa cepat benda berputar di sekitar sumbu rotasinya. Kecepatan sudut didefinisikan sebagai perubahan sudut yang terjadi dalam satu satuan waktu. Satu putaran lengkap (360 derajat) dalam satu detik setara dengan kecepatan sudut sebesar 2 rad/s.
Hukum kekekalan momentum sudut menyatakan bahwa dalam suatu sistem tertutup (tanpa torsi eksternal yang bekerja), momentum sudut total sistem akan tetap konstan.
Artinya, jika tidak ada momen luar yang bekerja pada sistem, total momentum sudut sistem akan tetap sama, meskipun benda-benda dalam sistem dapat berpindah momentum sudut di antara satu sama lain.
4. Hukum Newton untuk Rotasi
Hukum Newton untuk rotasi juga dikenal sebagai Hukum Kedua Newton untuk rotasi atau hukum dasar dinamika rotasi, memberikan hubungan antara torsi (τ) yang bekerja pada suatu benda dan percepatan sudut (α) yang dihasilkan oleh torsi tersebut.
Hukum ini mirip dengan Hukum Kedua Newton untuk gerakan translasi (gerakan lurus), tetapi berlaku khusus untuk gerakan rotasi. Hukum Newton untuk rotasi dinyatakan sebagai berikut:
τ = I.α
di mana:
τ = torsi yang bekerja pada benda (Nm)
I = momen inersia benda terhadap sumbu rotasinya (kgm²)
α = percepatan sudut benda yang dihasilkan oleh torsi (rad/s²)
5. Energi Kinetik Rotasi
Energi kinetik rotasi adalah energi kinetik yang dimiliki oleh suatu benda saat berputar mengelilingi sumbu rotasinya. Ketika benda bergerak rotasi, energi kinetiknya disebabkan oleh gerakan rotasional partikel-partikel penyusunnya.
Untuk menghitung energi kinetik rotasi (Ekr) dari suatu benda, kita menggunakan rumus:
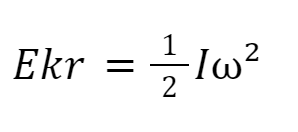
Rumus ini mirip dengan rumus energi kinetik translasi pada gerakan lurus:
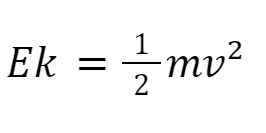
Perbedaan utama antara energi kinetik rotasi dan energi kinetik translasi adalah pada faktor momen inersia dan kecepatan yang berbeda. Energi kinetik rotasi bergantung pada momen inersia dan kecepatan sudut sedangkan energi kinetik translasi tergantung pada massa benda dan kecepatan translasi.
Ketika suatu benda bergerak dengan gerakan rotasi dan translasi, energi kinetik totalnya adalah jumlah dari energi kinetik rotasi dan energi kinetik translasinya.
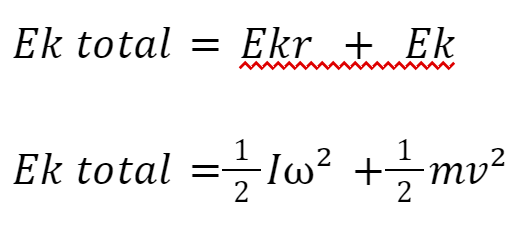
Pengaruh Dinamika Rotasi
Dinamika rotasi memiliki pengaruh yang signifikan dalam berbagai aspek kehidupan dan teknologi. Beberapa pengaruh penting yang sering kita temui dalam kehidupan sehari-hari antara lain:
1. Teknologi Mesin
Dasar dalam perancangan dan pemahaman berbagai mesin melibatkan gerakan rotasi, seperti mesin-mesin industri, mesin pembangkit listrik, mesin kendaraan, dan perangkat mesin lainnya. Penerapan prinsip-prinsipnya membantu meningkatkan efisiensi dan kinerja mesin-mesin ini.
2. Transportasi
Penerapan dinamika rotasi sangat penting dalam perancangan kendaraan. Khususnya dalam sistem suspensi, sistem roda, rem, dan stabilitas kendaraan yang memungkinkan insinyur untuk merancang sistem yang aman dan stabil, serta meningkatkan manuverabilitas kendaraan.
3. Ilmu Astronomi
Pengetahuan ini juga memungkinkan kita untuk memprediksi pergerakan objek astronomi dan memahami fenomena astronomi yang terkait dengan rotasi, seperti rotasi planet.
4. Olahraga
Dinamika rotasi sangat relevan dalam beberapa cabang olahraga, terutama dalam olahraga yang melibatkan gerakan rotasi, seperti renang, selancar, loncat indah, dan banyak lagi. Atlet dan pelatih menggunakan prinsip ini untuk meningkatkan teknik dan performa dalam olahraga-olahraga tersebut.
5. Industri Manufaktur
Dalam proses manufaktur, pemahaman dinamika rotasi digunakan untuk merancang dan mengoptimalkan perangkat seperti pemutar, kincir, roda gigi, dan perangkat rotasi lainnya. Ini membantu dalam produksi barang-barang dengan akurasi yang tinggi dan efisiensi produksi yang lebih baik.
6. Energi Terbarukan
Dalam konteks energi terbarukan, turbin angin dan generator listrik mengkonversi energi kinetik angin menjadi energi listrik. Maka dari itu, hal ini dapat memungkinkan pengembangan turbin angin yang lebih efisien dan andal.
7. Benda Angkasa
Pemahaman dinamika rotasi diperlukan untuk merencanakan dan mengontrol gerakan rotasi satelit dan wahana antariksa. Hal ini memungkinkan untuk menjaga orientasi dan stabilitas benda angkasa selama misi atau pengamatan.
Contoh Soal dan Pembahasannya
Sebuah cakram pejal dengan massa 2 kg dan jari-jari 0.5 m berputar dengan kecepatan sudut awal 4 rad/s. Pada saat t=3 s, torsi eksternal sebesar 3 Nm diberikan sehingga bekerja melawan arah rotasi. Hitunglah kecepatan sudut cakram setelah 3s dan percepatan sudut cakram pada saat itu.
Pembahasan:
m = 2 kg
r = 0,5 m
ω0 = 4 rad/s
t = 3s
τ = 3 Nm
Pertama, hitung dulu momen inersianya:
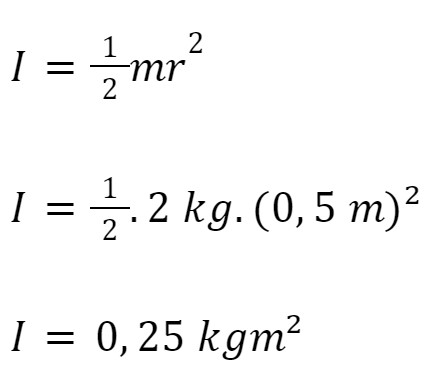
Kemudian mencari percepatan sudut cakram dengan rumus torsi:

Jadi, kecepatan sudut cakram setelah 3 s adalah 40 rad/s dan percepatan sudut cakram pada saat itu adalah 12 rad/s².
Kesimpulan
Dinamika rotasi diterapkan pada berbagai situasi, misalnya pada gerakan benda-benda berputar seperti roda, piringan, benda silindris, atau benda lain yang mengalami rotasi. Dengan menggunakan konsep yang berkaitan, kita dapat menganalisis pergerakan rotasi suatu benda dan merancang sistem yang berputar dengan efisien.
Selain itu, cabang ilmu fisika ini juga berperan dalam pemahaman tentang gerakan objek astronomi, sistem mekanik, dan banyak aplikasi lain dalam ilmu fisika dan teknik.

