Dalam statistika, salah satu konsep dan alat yang digunakan untuk menganalisis data adalah distribusi normal. Biasanya ini berfungsi untuk menggambarkan seberapa sering suatu kejadian terjadi dalam rentang tertentu dan pola penyebarannya. Apa saja parameter dan rumus fungsi di dalamnya?
Yuk, kita bahas tuntas materinya, lalu pelajari contoh soal dan pembahasannya di artikel ini.
Apa Itu Distribusi Normal?
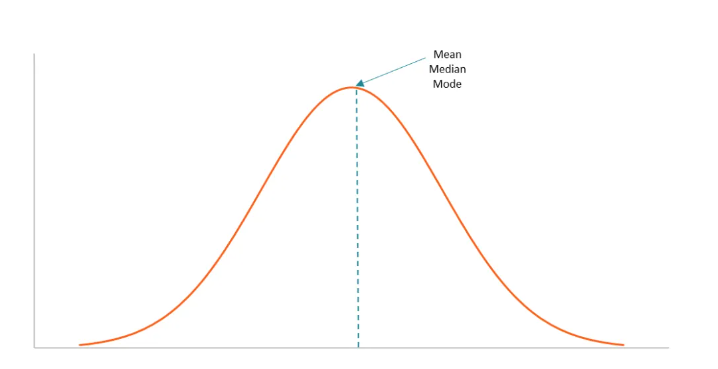
Distribusi normal, juga dikenal sebagai distribusi Gaussian atau distribusi bell curve, adalah salah satu distribusi probabilitas yang penting dalam statistika.
Penamaan distribusi bell curve diberikan karena distribusi normal digambarkan sebagai kurva lonceng yang simetris. Seperti lonceng, ia melandai di tepi dan memiliki puncak di tengah.
Jadi, distribusi ini menggambarkan distribusi data acak yang simetris, di mana sebagian besar data berkumpul di sekitar nilai tengah atau nilai rata-rata (mean), sedangkan data lainnya menyebar secara merata ke kedua sisi.
Artinya, kurva lonceng ini mengilustrasikan seberapa sering suatu kejadian atau data muncul dalam suatu rentang tertentu. Aplikasinya dalam kehidupan sehari-hari seperti untuk menggambarkan berbagai fenomena alam, data tinggi badan manusia, hasil tes, atau berat badan suatu populasi.
Sebagai contoh, pada kumpulan data berat badan suatu populasi yang besar, kemungkinan sebagian besar dari datanya memiliki berat badan rata-rata. Sementara itu, data berat badan yang sangat berat atau sangat ringan jumlahnya akan turun semakin sedikit mengikuti landaian.
Karakteristik dan Sifat Distribusi Normal
Distribusi normal memiliki beberapa karakteristik dan sifat penting yang perlu dipahami, yakni:
1. Simetri
Pertama, distribusi bell curve bersifat simetris. Artinya pada sekitar nilai mean sebagai titik tengah distribusi, grafik ini memiliki bentuk yang sama atau hampir sama di kedua sisi.
2. Unimodal
Selain itu, distribusi ini hanya memiliki satu puncak (mode). Oleh sebab itu, sebagian besar data berkumpul di sekitar nilai mean.
3. Memiliki Parameter yang Terdefinisi
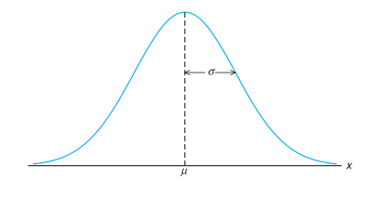
Kurva dengan distribusi berbentuk lonceng ini ditentukan sepenuhnya oleh dua parameter utama, yaitu nilai mean (μ) dan standar deviasi (σ). Kedua parameter inilah yang menggambarkan pusat dan sebaran data.
4. Kurva Mulus
Selanjutnya, bentuk kurvanya mulus. Bahkan tidak memiliki “puncak” atau “lembah” yang tajam.
5. Total Area di Bawah Kurva = 1
Karakteristik terakhirnya adalah kurva ini memiliki total area di bawah kurva sama dengan 1. Artinya, probabilitas total semua nilai dalam distribusi adalah 1.
Parameter dalam Distribusi Normal
Inilah dua parameter utama yang mendefinisikan distribusi normal, yakni:
1. Nilai Rata-Rata (Mean)
Mean (μ) atau nilai rata-rata adalah titik pusat dari suatu data, termasuk pada distribusi bell curve. Nilai rata-rata menunjukkan lokasi pusat data dan merupakan nilai ekspektasi dari distribusi tersebut.
Saat memahami sebaran data dalam distribusi normal, rujukan utama yang kita gunakan adalah nilai mean.
2. Standar Deviasi atau Simpangan (σ)
Sementara itu, standar deviasi (σ) mengukur sebaran data dalam suatu populasi termasuk data dalam distribusi bell curve. Semakin besar nilai standar deviasi, maka semakin besar sebaran data dari nilai mean.
Melalui standar deviasi, kita akan mengetahui tingkat dispersi atau variasi dalam populasi data.
Aturan Empiris untuk Distribusi Normal
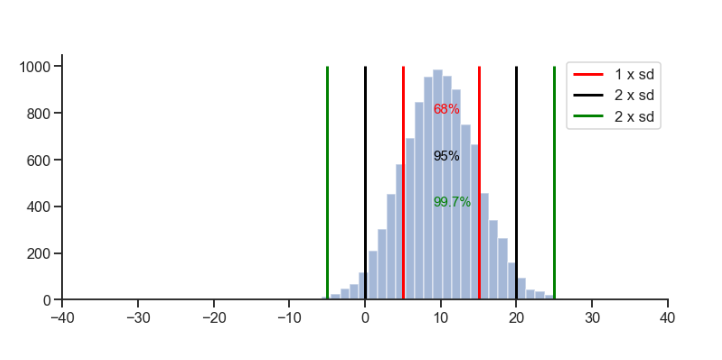
Dalam penerapannya, distribusi bell curve mengikuti aturan empiris yang penting untuk memahami bagaimana data terdistribusi dalam kurvanya. Aturan empiris ini dikenal sebagai aturan 68-95-99.7, yang menyatakan bahwa:
- Sekitar 68% data berada dalam satu standar deviasi dari mean.
- Sekitar 95% data berada dalam dua standar deviasi dari mean.
- Sementara sekitar 99.7% data berada dalam tiga standar deviasi dari mean.
Kemudian, dalam penerapannya, ketiga aturan ini memberikan gambaran tentang sebaran data di dalamnya. Semakin besar standar deviasi, semakin lebar sebaran data dari nilai mean.
Baca Juga : Analisis Data Adalah: Pengertian, Tujuan, dan Contoh
Rumus dan Fungsinya
Distribusi normal memiliki dua bentuk utama, yaitu yang umum dan yang standar. Begini rumus fungsi untuk masing-masingnya:
1. Fungsi Distribusi Normal Umum (Distribusi x)
Pada jenis yang umum, parameter mean (μ) dan standar deviasi (σ) dari data di dalamnya dapat bervariasi. Fungsi distribusi normal umum dinyatakan sebagai:
f(x) = (1/ (σ√2π))e^(– ((x−μ)2/2σ2))
di mana f(x) adalah fungsi distribusi probabilitas, σ adalah standar deviasi, μ adalah mean, dan x adalah variabel acak.
2. Fungsi Distribusi Normal Standar (Distribusi z)
Sedangkan jenis yang standar adalah versi khusus dengan mean (μ) = 0 dan standar deviasi (σ) = 1. Jadi, fungsinya dinyatakan sebagai:
f(z) = (1/√2π))e^(–z2/2)
di mana f(z) adalah fungsi distribusi probabilitas, dan z adalah variabel acak yang sudah mengalami standardisasi.
3. Nilai z (Variabel Standar)
Kemudian, untuk menghitung nilai z, yang mengindikasikan seberapa jauh nilai suatu data dari nilai rata-rata dalam kurva, gunakan rumus berikut:
z = (x−μ)/σ
di mana:
- z adalah nilai z (variabel standar).
- x adalah nilai individu.
- μ adalah nilai rata-rata (mean).
- σ adalah standar deviasi.
Rumus ini akan menghasilkan nilai z yang menunjukkan seberapa banyak standar deviasi suatu nilai individu dari mean.
4. Nilai x (Variabel Individu)
Jika kita memiliki nilai z dan ingin menemukan nilai x yang sesuai, maka gunakan rumus inversnya:
x = μ + z ⋅ σ
di mana:
- x adalah nilai data individu yang ingin dihitung.
- μ adalah nilai rata-rata (mean).
- z adalah nilai z atau variabel standar.
- σ adalah standar deviasi.
Namun, dalam praktiknya, perhitungan probabilitas dan nilai-nilai dari distribusi normal sering menggunakan tabel distribusi z, yaitu jenis yang standar, atau menggunakan perangkat lunak statistik.
Contoh Soal dan Pembahasan

Setelah mempelajari seluruh teori yang berhubungan dengan distribusi bell curve, mari kita lihat beberapa contoh soal yang melibatkannya. Simak juga pembahasan bagaimana cara menghitungnya.
1. Contoh Soal 1
Sebuah perusahaan elektronik memproduksi lampu LED dengan kecerahan rata-rata 1200 lumen dan standar deviasi untuk kecerahan rata-ratanya adalah 50 lumen. Berapa persen lampu LED yang diproduksi dengan kecerahan lebih dari 1300 lumen?
Pembahasan:
Untuk menghitung persentase lampu LED dengan kecerahan lebih dari 1300 lumen, kita perlu menghitung nilai z (variabel standar) terlebih dahulu:
z = (1300−1200)/50 =2
Kemudian, kita bisa merujuk ke tabel distribusi normal standar atau menggunakan perangkat lunak statistik untuk menemukan probabilitas P(z>2).
f(z) = (1/√2π))e^(–z2/2)
P(Z>2) = (1/√2π))e^(–22/2)
Dari perhitungan lebih lanjut (yang bisa kita hitung menggunakan perangkat lunak statistik seperti Excel, kita dapat mengetahui bahwa P(z>2) ≈ 0,0228 atau sekitar 2,28%.
Jadi, lampu LED yang diproduksi dengan kecerahan lebih dari 1300 lumen adalah sekitar 2,28%.
2. Contoh Soal 2
Sebuah toko pakaian memiliki rata-rata penjualan harian 300 produk dengan standar deviasi sebesar 50 produk. Berapa persen kemungkinan toko tersebut akan menjual kurang dari 250 produk dalam satu hari?
Pembahasan:
Untuk menghitung probabilitas penjualan kurang dari 250 produk dalam satu hari, kita perlu menghitung nilai z (variabel standar) terlebih dahulu:
z = (x−μ)/σ
z= (250−300)/ 50 = −1
Kemudian, kita perlu mencari probabilitas P(z<−1)
f(z) = (1/√2π))e^(–z2/2)
P(z> -1) = (1/√2π))e^(12/2)
Dari perhitungan lebih lanjut (yang bisa kita hitung menggunakan perangkat lunak statistik seperti Excel, kita dapat mengetahui bahwa P(z> -1) ≈ 0,1587 atau sekitar 15,87%.
Jadi, kemungkinan toko akan menjual kurang dari 250 produk dalam satu hari yaitu sekitar 15,87%.
Baca Juga : Teknik Pengumpulan Data: Pengertian, Jenis, dan Contohnya
Pahami Sifat, Rumus, serta Fungsi Distribusi Normal!
Kesimpulannya, kurva distribusi normal penting untuk kita memahami sebaran data dan perhitungan probabilitasnya. Dengan karakteristiknya yang simetris, serta parameter mean dan standar deviasi, kurva ini memberikan kerangka yang kuat untuk menganalisis berbagai data yang terdistribusi secara normal.
Ketika menganalisis statistiknya, pemahaman atas karakteristik, parameter, serta rumus dan fungsinya sangatlah penting. Pasalnya, faktor-faktor tersebut memungkinkan kita untuk menghitung probabilitas dan menggambarkan bagaimana sebaran datanya.

