Dalam bidang ilmu matematika, kamu pasti sering menemukan istilah konstanta sebagai suatu fungsi untuk memecahkan persoalan matematis. Lalu, apa yang menjadi maksud dari konsep ini dan bagaimana penerapannya? Cari tahu jawabannya di artikel ini, yuk!
Apa Itu Konstanta?
Secara harfiah, arti dari konstanta mengacu pada angka, nilai, atau simbol yang memiliki besaran tetap dan tidak pernah berubah. Bentuk dari entitas ini dapat berupa angka bulat, desimal, atau bahkan pecahan.
Bilangan matematika ini biasanya dilambangkan dengan “c” untuk mewakili nilai tetapnya. Nilai dari simbol c ini dapat memiliki nilai yang berbeda-beda dalam tiap kasus, namun ia tidak akan terpengaruh oleh perubahaan variabel dalam suatu persamaan.
Penerapan lambang c ini bisa kamu temukan di persamaan umum garis lurus, yaitu y = mx + c. Pada persamaan tersebut, y adalah persamaan garis lurus, m adalah kemiringan garis, x adalah variabel, dan c sendiri sebagai nilai tetapnya. Jika y = 2x + 1, maka angka 1 adalah suatu konstanta.
Dalam konteks matematika, semua angka adalah nilai tetap, termasuk nilai-nilai seperti bilangan real, bilangan asli, dan bilangan bulat. Misalnya, Ani membaca 5 lembar halaman buku pada hari Senin dan 8 lembar halaman pada hari Selasa. Lantas, berapa jumlah halaman yang Ani baca dalam dua hari?
Untuk menemukan jumlah total halaman yang terbaca oleh Ani, kamu harus menjumlahkan 5 dan 8 yang merupakan bilangan konstan. Sehingga, jumlah total halaman yang Ani baca dalam dua hari adalah 5 + 8 = 13 halaman.
Penerapan konsep ini juga bisa kamu temukan dalam persamaan aljabar, misalnya pada 5x + 4y = 12. Dari persamaan tersebut, x dan y adalah variabel yang kuantitasnya dapat berubah, 5 adalah koefisien x, 4 adalah koefisien y, sedangkan 12 dan 1 adalah konstanta.
Mengapa 5 dan 4 bukan merupakan nilai tetap? Jawabannya adalah karena bilangan tersebut merupakan bilangan koefisien atau bilangan yang tidak berdiri sendiri, serta memiliki variabel x dan y yang mengikutinya.
Cara Mengenali Konstanta dalam Aljabar
Berikut ini beberapa cara yang bisa kamu ikuti untuk mengidentifikasi bilangan yang nilainya tetap:
- Nilainya diketahui.
- Merupakan bilangan yang berdiri sendiri.
- Jika nilainya tidak diketahui, maka angka tersebut adalah angka yang ditetapkan.
- Melibatkan bentuk pecahan, desimal, bilangan bulat, dan semua bilangan real.
- Eksponen atau pangkat bukanlah konstanta. Misalnya dalam bilangan 25, angka 5 bukanlah nilai tetap.
Fungsi Konstanta
Istilah dari bilangan tetap juga berguna untuk memetakan setiap angka ke fungsi konstan. Singkatnya, fungsi konstan adalah fungsi yang outputnya tidak tergantung pada nilai inputnya.
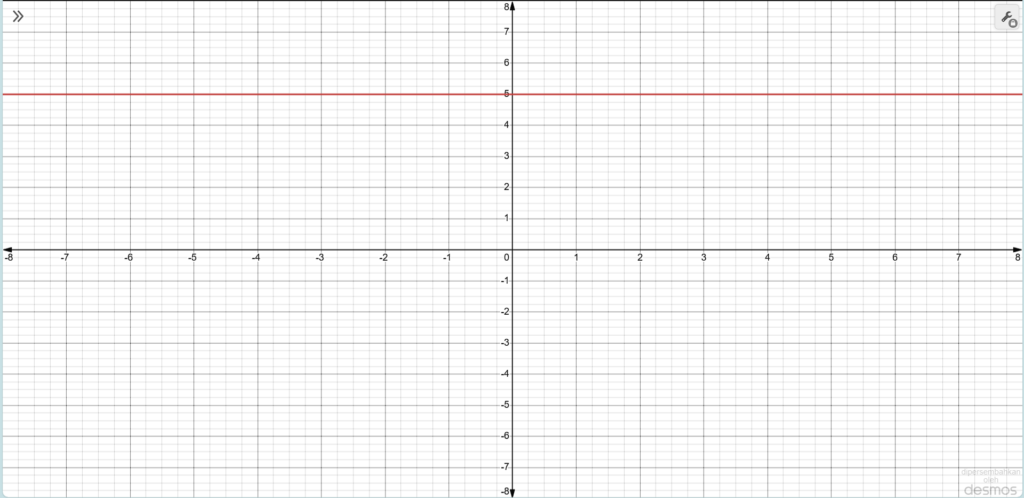
Misal, f(x) = 5. Persamaan tersebut merupakan fungsi konstan karena variabel utamanya adalah x, sedangkan angka 5 tidak bergantung pada x. Tidak peduli nilai apa yang kamu masukkan untuk x, output dari fungsi akan tetap bernilai 5.
Apabila nilai fungsi f(x) = 5 digambarkan pada grafik, maka grafik tersebut akan memuat garis horizontal yang sejajar dengan sumbu x, atau dapat terlihat garis merah pada gambar di bawah ini:
Jenis-Jenis Konstanta dalam Matematika
Secara umum, ada berbagai jenis konstanta yang perlu kamu kenali dalam matematika. Berikut ini adalah macam-macamnya:
1. Pi (π)
Nilai pi (π) adalah bilangan matematika yang digunakan untuk menghitung perbandingan keliling lingkaran dengan diameter (d) atau keliling dengan jari-jari (r) lingkaran. Nilai pi adalah bilangan irasional, yang berarti bahwa desimalnya tidak berulang dan tidak berakhir dengan nilai sama dengan 3,14159265359.
2. Bilangan Euler (e)
Bilangan Euler (e) adalah salah satu bilangan matematika yang sangat penting dalam menunjukkan fungsi eksponensial atau konsep dasar dari logaritma dan kalkulus. Dalam notasi matematika, bilangan Euler dapat dinyatakan sama dengan 2,7182818284.
3. Bilangan Imajiner (i2)
Bilangan imajiner adalah jenis bilangan dalam matematika yang berguna untuk mewakili sebagai bilangan riil. Selain itu, bilangan ini juga terdefinisi sebagai hasil perkalian dari bilangan riil dengan unit imajiner (i). Serta menggambarkan nilai yang melibatkan akar kuadrat dari -1, sehingga i2 = -1.
4. Akar 2 (√2)
Secara sederhana, akar kuadrat dari 2 (√2) adalah konstanta Phytagoras yang jika dikuadratkan mana akan menghasilkan nilai 2. Bilangan ini juga termasuk bilangan irasional karena nilai desimalnya tidak berulang dan tidak berakhir untuk menghitung panjang diagonal persegi, yang mana nilainya kira-kira sebesar 1,4142135623.
5. Rasio Emas atau Phi (φ)
Berdasarkan konsep matematika, phi (φ) adalah bilangan matematika yang didefinisikan sebagai bilangan irasional dengan nilai sekitar 1,618033988749895. Phi sering dikaitkan dengan Golden Ratio yang merupakan perbandingan dua angka antara jumlah (a + b) dan a sama dengan perbandingan antara a dan b.
Dua nilai akan termasuk dalam hubungan Golden Ratio apabila perbandingan antara jumlah kedua nilai tersebut terhadap nilai yang besar sama dengan perbandingan antara nilai besar terhadap nilai kecil.
Unsur-Unsur Matematika Aljabar
Aljabar adalah salah satu cabang matematika yang menunjukkan konsep persamaan, sistem bilangan, atau simbol untuk menyatakan atau memanipulasi persoalan matematika. Aljabar juga perlu beberapa unsur penting lain yang dapat mendukung fungsinya secara utuh, di antaranya adalah:
1. Variabel
Variabel adalah istilah yang dapat berubah atau berbeda dari waktu ke waktu karena unsur ini tidak akan memiliki nilai tetap. Beberapa contoh dari variabel adalah tinggi dan berat. Tinggi dan berat seseorang tidak akan tetap konstan dan akan bervariasi seiring waktu.
Jika bilangan tetap (dilambangkan dengan notasi “c”) ditunjukkan dengan nilai numerik, maka lain halnya dengan variabel yang mana dapat ditunjukkan dengan nilai alfabet a-z. Selain itu, ada juga simbol variabel lain, seperti θ dan φ yang berguna mewakili variabel untuk sudut pada geometri atau trigonometri.
Pentingnya variabel dalam aljabar adalah untuk menghubungkan suatu kuantitas tanpa mengetahui nilai spesifik dari kuantitas tersebut. Sebagai contoh, kamu bisa menggunakan variabel untuk mewakili panjang, lebar, dan tinggi bentuk geometris tanpa mengetahui pengukuran yang tepat.
2. Koefisien
Koefisien adalah bilangan bulat yang ditulis bersama dengan variabel atau dikalikan dengan variabel. Dengan kata lain, koefisien adalah faktor numerik dari suatu istilah yang mengandung konstanta dan variabel. Misalnya, dalam fungsi 2x, angka 2 adalah koefisien.
Cara mudah untuk memahami koefisien adalah dengan mengenali karakteristiknya. Koefisien selalu melekat pada variavel. Tidak ada nilai 0 sebagai koefisien, karena nilai suku pada angka 0 sebagai koefisiennya adalah 0.
Variabel yang tidak memiliki angka di depannya adalah koefisien 1. Sebagai contoh, dalam persamaan x+ 2y, koefisien dari variabel x adalah 1, sedangkan koefisien dari variabel y adalah 2.
3. Suku
Suku adalah bagian dari persamaan aljabar yang terdiri dari konstanta, variabel, koefisien, atau kombinasi ketiganya. Kegunaan dari suku adalah membentuk persamaan polinomial, contohnya seperti 6x2+ 5x + 7.
Karakteristik suku adalah terhubungnya masing-masing unsur-unsur aljabar yang ada, lengkap dengan operasi matematika seperti penambahan, pengurangan, pembagian, atau perkalian. Dengan demikian, operasi matematika ini memegang peran penting untuk membentuk suku dalam persamaan aljabar.
Akan tetapi, suku dapat terbagi menjadi suku 1, suku 2, suku 3, hingga membentuk persamaan polinomial yang lebih banyak. Kategori suku 1 adalah jika bentuk aljabar tidak terhubung dengan operasi matematika. Beberapa contoh untuk suku 1 adalah 2x, -5ab, dan 4x².
Suku 2 adalah bentuk aljabar yang terhubung dengan satu operasi matematika, misalnya 6x+10, 4x²-14x, dan 6ad-2. Lain halnya dengan suku 3 adalah bentuk aljabar yang terhubung dengan dua operasi matematika, seperti 9x²+6x-2 dan 17x²-3x-12.
Baca Juga : Sifat Logaritma Beserta Rumus dan Cara Mengerjakannya
Contoh Soal Konstanta dalam Aljabar
Berikut ini adalah beberapa contoh soal yang melibatkan konstanta dalam aljabar:
1. Contoh Soal 1
Tentukan variabel, suku, konstanta, dan koefisien dari persamaan aljabar 9x + 2y – 3!
Pembahasan:
- Variabel adalah x dan y.
- Suku 1 adalah 9x, 2y, dan 3.
- Konstanta adalah 3.
- Koefisien adalah 9 dan 2.
2. Contoh Soal 2
Temukan nilai tetap dari persamaan 4x + 3 = 9y – 10
Pembahasan:
Pertama-tama, kamu harus menyederhanakan persamaan tersebut seperti berikut ini:
4x + 3 = 9y – 10
4x – 9y = -10 – 3
4x – 9y = -13
Sehingga, konstanta pada persoalan di atas adalah -13.
3. Contoh Soal 3
Ryan memiliki 5 apel dan Thea memiliki 12 apel lebih banyak dari Doni. Berapa nilai tetap dan variabel dalam skenario ini?
Pembahasan:
Sebelumnya, mari pahami berapa banyak apel yang dimiliki masing-masing.
- Ryan memiliki 5 apel.
- Katakanlah, Doni memiliki apel. Apel milik Doni sebagai variabel x karena tidak diketahui nilai tetapnya.
- Apel miliki Thea 12 kali lebih banyak dari apel milik Doni. Jadi, Thea memiliki x + 12 apel.
Dari penjabaran di atas, satu-satunya yang termasuk bilangan tetap adalah 5, karena jumlah apel milik Thea dan Doni bergantung pada variabel.
Baca Juga : Limit Tak Hingga: Pengertian, Sifat, Fungsi, dan Contoh Soal
Pahami Konstanta untuk Belajar Matematika yang Lebih Mudah!
Pada intinya, konsep matematika seperti konstanta beserta unsur-unsur matematika lainnya seperti koefisien, variabel, fungsi, dan suku merupakan satu kesatuan yang sangat penting dalam perhitungan aljabar. Maka dari itu, kamu harus memahami apa arti dan perannya.Kerjakan latihan-latihan dan soal-soal yang melibatkan penggunaan konstanta. Dengan berlatih, Anda akan menjadi lebih terbiasa dalam mengerjakan persamaan matematika yang melibatkan konsep bilangan yang kompleks. Selamat belajar!

