Dalam ilmu matematika dan geometri, pengertian sudut tumpul menjadi salah satu konsep dasar yang penting untuk dipahami. Sebab, konsepnya memungkinkan Anda untuk mengenali pola dan hubungan antara sudut-sudut dalam berbagai bentuk dan struktur geometris.
Selain itu, sudut ini memiliki sifat-sifat khusus yang membedakannya dari jenis sudut lainnya. Artikel ini akan menjelaskan pengertian sudut tumpul, sifat atau cirinya, serta memberikan beberapa contoh soal yang dapat membantu Anda memahami konsep ini dengan lebih baik.
Pengertian Sudut Tumpul
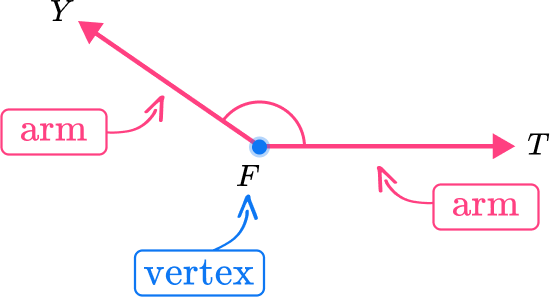
Secara teori, pengertian sudut tumpul adalah sudut yang memiliki ukuran lebih besar dari 90 derajat tetapi kurang dari 180 derajat. Sudut ini terbentuk ketika dua garis memanjang dari titik yang sama saling berpotongan dan melebihi sudut siku-siku.
Anda bisa menggunakan simbol (∠) untuk memberi nama sudut. Misalnya, sudut tumpul dapat dinamai sebagai ∠YFT atau ∠TFY. Nah, jika Anda membayangkan sudut 90 derajat, maka Anda dapat melihat bahwa sudut tumpul (∠YFT) lebih besar dari 90 derajat tetapi kurang dari 180 derajat (garis lurus).
Untuk memastikan suatu sudut merupakan sudut tumpul, Anda dapat mengukurnya dengan busur derajat. Kemudian, sudut tumpul dapat Anda temukan pada berbagai bentuk geometri, seperti oktagon, jajar genjang, trapesium, atau ketika dua garis lurus bersilangan.
Jenis-jenis Sudut
Terdapat beberapa jenis sudut yang dapat dibedakan berdasarkan besar sudut dan sifat-sifat khususnya. Berikut adalah beberapa jenisnya:
- Lancip: Merupakan jenis sudut dengan ukuran lebih kecil dari 90 derajat.
- Siku-siku: Merupakan jenis sudut dengan ukuran tepat 90 derajat.
- Tumpul: Merupakan jenis sudut yang lebih besar dari 90 derajat tetapi lebih kecil dari 180 derajat.
- Lurus: Merupakan jenis sudut dengan ukuran 180 derajat, sehingga membentuk garis lurus.
- Sudut refleks atau besar: Merupakan jenis sudut yang lebih dari sudut lurus, yaitu memiliki ukuran lebih dari 180 derajat tetapi kurang dari 360 derajat.
- Sudut penuh: Merupakan jenis sudut dengan ukuran 360 derajat, sehingga mencakup putaran penuh.
Untuk memahami pengertian sudut tumpul dan sudut-sudut lain secara visual, bayangkan sebuah lingkaran dengan pusat di titik tengah sudut. Sudut lancip akan terletak di bagian dalam lingkaran, kemudian sudut siku-siku akan berada di tepi lingkaran.
Sedangkan sudut lurus akan membentuk garis lurus yang melintasi tepi lingkaran, sudut refleks akan berada di luar lingkaran, dan sudut penuh akan mencakup semua lingkaran. Dengan pemahaman tentang istilah-istilah tersebut, Anda dapat menggambarkan sudut-sudut dengan lebih mudah dalam berbagai situasi geometri.
Ciri-ciri Sudut Tumpul
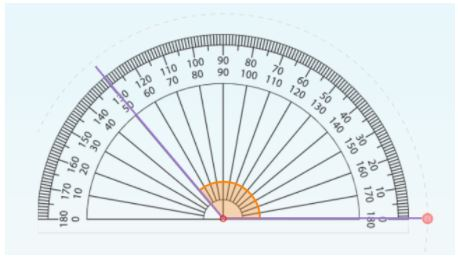
Seperti yang telah kami sebutkan di awal artikel, sudut tumpul adalah salah satu jenis sudut dalam geometri yang memiliki ciri-ciri khusus yang membedakannya dari jenis sudut lainnya. Berikut adalah ciri-ciri sudut tumpul:
- Sudut-sudut ini berukuran antara 90 derajat dan 180 derajat.
- Pengertian sudut tumpul lebih besar dari sudut siku-siku (berukuran 90 derajat) dan sudut lancip (berukuran kurang dari 90 derajat), tetapi lebih kecil dari sudut lurus (180 derajat). Sehingga, jika Anda mengurutkan sudut dari yang terkecil hingga terbesar, itu akan menjadi lancip < siku < tumpul < lurus.
- Secara visual, sudut tumpul memiliki ukuran yang lebih besar daripada seperempat lingkaran, namun lebih kecil daripada setengah lingkaran. Jadi, jika Anda membagi lingkaran menjadi empat bagian, sudut tumpul akan selalu menempati antara 1/4 dan 1/2 lingkaran.
- Selalu ada sudut tumpul dalam segitiga tumpul.
Apa itu Segitiga Tumpul?
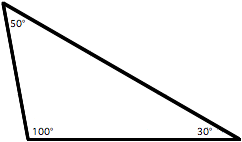
Segitiga tumpul adalah jenis segitiga di mana memiliki salah satu sudut yang bersifat tumpul. Namun, penting untuk Anda catat bahwa segitiga tumpul sebenarnya tidak sepenuhnya terdiri dari sudut-sudut tumpul.
Sebuah segitiga yang hanya memiliki sudut tumpul tidak akan membentuk sebuah segitiga. Sebaliknya, dalam segitiga tumpul hanya ada satu sudut yang memiliki ukuran lebih besar dari 90 derajat.
Sedangkan dua sudut lainnya adalah sudut-sudut lancip atau sudut-sudut yang lebih kecil dari 90 derajat. Dengan demikian, meskipun terdapat sudut tumpul dalam segitiga tumpul, segitiga itu sendiri masih terdiri dari kombinasi sudut-sudut tumpul dan sudut-sudut lancip.
Baca Juga : Mengenal Perbedaan Sumbu Simetri Lipat dan Simetri Putar
Contoh Soal Terkait Sudut Tumpul
Berikut contoh soal untuk mencari sudut tumpul:
1. Contoh Soal 1
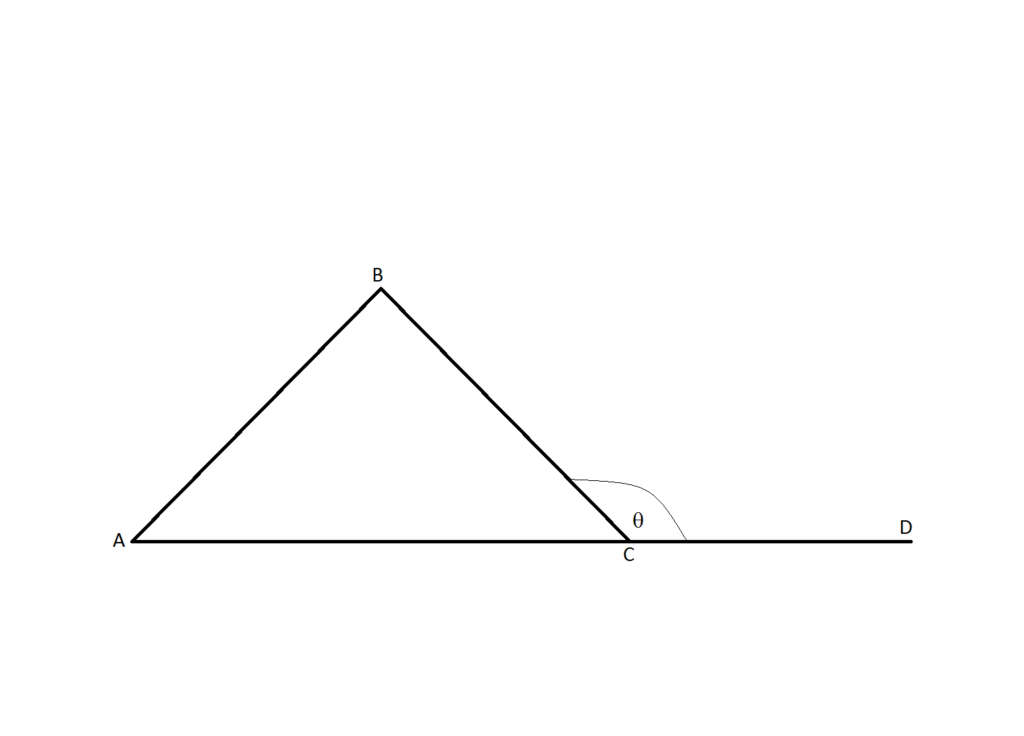
Pada gambar tersebut, diketahui ∠A=42° dan ∠B=76°. Lantas, berapa ukuran θ?
Jawab:
Ketika Anda memiliki sebuah segitiga, total sudut interior segitiga selalu menambah hingga 180°. Oleh karena itu, Anda dapat menggunakan informasi ini untuk mencari ukuran sudut-sudut yang tidak diketahui.
Pertama, carilah ukuran ∠C dengan menggunakan persamaan:
∠C = 180° – (∠A + ∠B)
∠C = 180° – (42° + 76°) = 180° – 118° = 62°
Sekarang, carilah ukuran sudut θ. Sudut θ adalah sudut eksterior segitiga yang berhubungan dengan sudut C. Menurut pengertian sudut tumpul, ukuran sudut eksterior segitiga adalah jumlah dari dua sudut interior yang berlawanan dengannya.
Jadi, Anda dapat menulis:
θ = 180° – ∠C
θ = 180° – 62° = 118°
Jadi, ukuran sudut θ adalah 118°. Ini berarti bahwa sudut θ memiliki ukuran 118° dan merupakan sudut eksterior segitiga yang terbentuk oleh sudut B dan sudut C.
2. Contoh Soal 2
Biarkan ukuran (dalam derajat) dari tiga sudut segitiga menjadi x, y, dan z. Jika y = 2z, dan z = 0,5x – 30, maka berapa ukuran (dalam derajat) dari sudut terbesar dalam segitiga?
Jawab:
Ukuran dari tiga sudut adalah x, y, dan z. Karena jumlah ukuran sudut dalam segitiga apa pun harus bernilai 180 derajat, maka diketahui bahwa x + y + z = 180.
Anda dapat menggunakan persamaan ini, bersama dengan dua persamaan lain yang diberikan, untuk membentuk sistem persamaan ini:
x + y + z = 180
y = 2z
z = 0,5x – 30
Jika Anda dapat menyelesaikan y dan x dalam hal z, maka Anda dapat mengganti nilai-nilai ini ke dalam persamaan pertama dan membuat persamaan hanya dengan satu variabel.
Karena Anda sudah diberitahu bahwa y = 2z, Anda sudah memiliki nilai y dalam hal z. Anda harus menyelesaikan persamaan z = 0,5x – 30 untuk x dalam hal z.
Pertama, tambahkan tiga puluh ke kedua sisi.
z + 30 = 0,5x
Kemudian, kalikan kedua sisi oleh 2
2(z + 30) = 2z + 60 = x
x = 2z + 60
Sekarang Anda memiliki nilai x dan y dalam hal z. Gantilah nilai-nilai ini untuk x dan y ke dalam persamaan x + y + z = 180.
(2z + 60) + 2z + z = 180
5z + 60 = 180
5z = 120
z = 24
Karena y = 2z, maka y = 2(24) = 48. Anda juga telah menentukan sebelumnya bahwa x = 2z + 60, jadi x = 2(24) + 60 = 108.
Dengan demikian, ukuran dari tiga sudut segitiga adalah 24, 48, dan 108. Pertanyaannya meminta yang terbesar dari langkah-langkah ini, yaitu 108. Jawabannya adalah 108.
Contoh Sudut Tumpul Dalam Kehidupan Sehari-hari
Ada beberapa contoh sudut tumpul yang dapat Anda temukan dalam kehidupan sehari-hari. Beberapa contohnya adalah sebagai berikut:
- Sudut yang dibentuk oleh jarum jam analog, misalnya pukul 3:35, dapat menjadi sudut tumpul, sesuai dengan pengertian sudut tumpul bahwa ukurannya akan berada antara 90 derajat dan 180 derajat.
- Ketika seorang balerina meregangkan kakinya dengan amplitudo yang besar, sudut yang terbentuk oleh kakinya dapat menjadi sudut tumpul.
- Jika seseorang telah memakan lebih dari seperempat pizza tetapi kurang dari setengahnya, maka bagian yang hilang akan membentuk sudut tumpul pada sisa pizza.
- Ketika kipas dibuka dengan lebar, itu membentuk sudut tumpul. Namun, jika kipas sedikit ditutup, maka sudutnya menjadi sudut kanan, dan jika ditutup lebih banyak tetapi tidak sepenuhnya, maka itu menjadi sudut tumpul.
- Sudut yang dibentuk oleh lengan excavator saat menggali tanah dapat menjadi sudut tumpul. Dengan pengertian sudut tumpul ini, excavator dapat mencapai kedalaman yang lebih besar dalam penggalian daripada jika sudutnya lebih kecil.
Sudah Paham dengan Pengertian Sudut Tumpul?
Dalam kesimpulannya, pengertian sudut tumpul adalah salah satu jenis sudut yang memiliki ukuran antara 90 derajat dan 180 derajat. Dalam kehidupan sehari-hari, Anda dapat menemukan contoh-contoh sudut tumpul pada berbagai objek dan situasi.
Memahami sudut tumpul dapat membantu Anda mengenali dan menggambarkan perbedaan sudut-sudut yang ada di sekitar Anda, serta memahami sifat-sifat geometris yang terkait. Visualisasi membantu Anda mengingat sifat-sifat sudut tumpul dengan lebih baik.
Bila perlu, lakukan latihan dengan mengerjakan soal-soal terkait sudut tumpul. Cara ini membantu Anda mengaplikasikan konsep dalam berbagai konteks dan menguji pemahaman Anda.

