Persamaan Linear Dua Variabel: Metode Grafik dan Substitusi

Dalam matematika, persamaan linear dua variabel merupakan konsep yang penting di mana menggunakan dua metode penting seperti metode grafik dan metode substitusi. Metode grafik melibatkan pembuatan grafik dari persamaan linear dan menemukan titik potongnya untuk menentukan solusinya. 

Sementara itu, metode substitusi melibatkan penggantian salah satu variabel dalam persamaan untuk mencari nilai variabel lainnya. Dengan memahami kedua metode ini, Anda akan memiliki dasar yang kokoh dalam menyelesaikan persamaan linear dengan lebih mudah. Ketahui informasi selengkapnya di bawah ini!

Definisi Persamaan Linear Dua Variabel

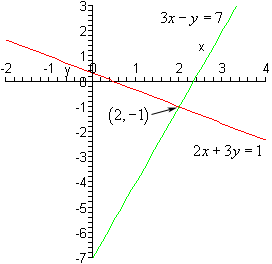
Persamaan linear dua variabel adalah bentuk persamaan matematika dengan melibatkan dua variabel yang memiliki derajat atau pangkat bernilai 1. Biasanya, persamaan ini ditulis dalam bentuk ax + by = c.

Pada persamaan tersebut, a, b, dan c adalah konstanta, sedangkan x dan y adalah variabel yang ingin dicari nilainya. Persamaan linear dalam dua variabel menggambarkan hubungan antara dua variabel melalui garis lurus yang disebut sebagai grafik. 

Dalam konteks ini, grafik berguna untuk menyelesaikan persamaan yang ada, di mana terdapat variabel yang tidak diketahui. Kamu bisa membuat grafik garis yang sesuai dengan persamaan tersebut pada sistem koordinat Cartesius. 

Persamaan linear dua variabel sering digunakan dalam berbagai bidang, seperti matematika, fisika, ekonomi, dan ilmu sosial. Misalnya, dalam ekonomi, persamaan linear ini dapat berguna untuk menganalisis hubungan antara pendapatan dan pengeluaran. 

Selain itu, dalam matematika, sering kali persamaan linear menjadi dasar untuk memahami dan memecahkan sistem persamaan linear yang lebih kompleks. Misalnya pada situasi di mana kamu perlu menemukan nilai-nilai variabel yang memenuhi beberapa persamaan secara bersamaan.

Jenis Sistem Linear

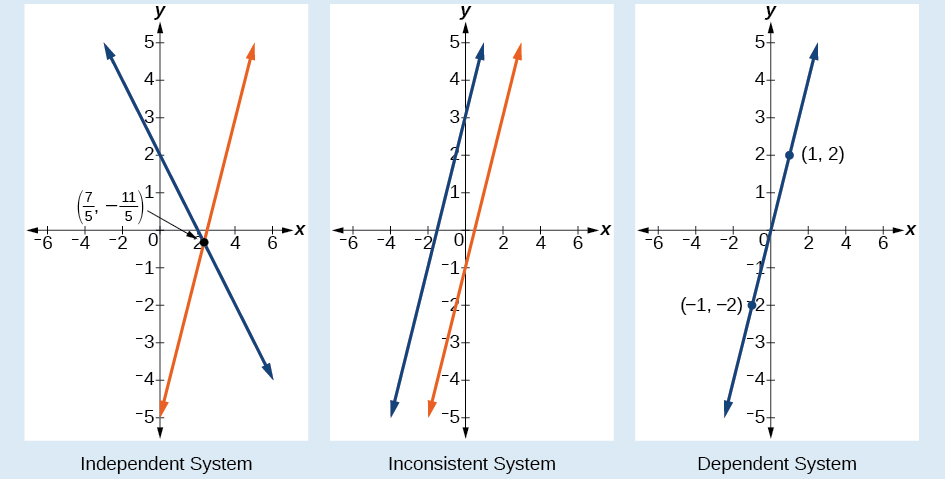
Secara teori, terdapat tiga jenis sistem persamaan linear dua variabel yang wajib kamu pelajari, di mana masing-masing jenis memiliki solusi yang berbeda. Berikut ini adalah penjelasannya:

1. Sistem Independen 

Sistem independen adalah sistem persamaan di mana ada tepat satu pasangan solusi (x, y). Dalam representasi grafis, persamaan ini terjadi ketika dua garis berpotongan pada satu titik tunggal yang mana menjadi satu-satunya solusi persamaan tersebut.

2. Sistem yang Tidak Konsisten 

Kemudian, sistem yang tidak konsisten atau inconsistent system adalah sistem persamaan di mana tidak ada solusi yang memenuhi kedua persamaan. Dalam representasi grafis, persamaan ini terjadi ketika dua garis paralel tidak pernah berpotongan. 

Lantaran tidak ada garis-garis yang saling bertemu, tidak ada titik yang memenuhi kedua persamaan tersebut, sehingga sistem tidak memiliki solusi. Dengan begitu, sistem persamaan tidak memiliki nilai x dan y yang memenuhi keduanya secara bersamaan.

3. Sistem Dependen 

Terakhir, sistem dependen adalah sistem persamaan di mana terdapat banyak solusi tanpa batas. Dalam representasi grafis, persamaan ini terjadi ketika dua garis yang mewakili persamaan tersebut bertepatan atau berada di atas satu sama lain. 

Dalam hal ini, setiap pasangan koordinat pada garis tersebut merupakan solusi yang memenuhi kedua persamaan. Selain itu, karena garis-garis ini bertepatan, maka tidak ada batasan pada jumlah solusi yang mungkin terbentuk.

Metode Grafik pada Sistem Persamaan Linear Dua Variabel

Pada dasarnya, metode grafik untuk persamaan linear dua variabel adalah suatu pendekatan matematis dalam menyelesaikan sistem persamaan dengan menggambarkan grafik dari setiap persamaan linear yang terlibat. 

Solusi sistem persamaan linear bisa ditemukan dengan mencari titik potong (interseksi) dari grafik-grafik tersebut. Adapun langkah-langkahnya adalah sebagai berikut:

1. Susun persamaan linear dalam bentuk umum y = mx + c, di mana m adalah koefisien kemiringan dan c adalah konstanta.
2. Kemudian, buat grafik untuk setiap persamaan linear dengan menggunakan koefisien kemiringan dan konstanta yang sesuai.
3. Setelah itu, tentukan titik potong grafik sebagai solusi sistem persamaan linear.
4. Jika ada lebih dari satu titik potong atau tidak ada titik potong, maka sistem persamaan linear dapat dikatakan tidak memiliki solusi unik atau tidak ada solusi.

Contoh Soal Persamaan Linear Dua Variabel dengan Penyelesaian Metode Grafik

Misalkan kamu punya sistem persamaan linear sederhana x + y = 3; x + 0 = 1. Nah, kamu diminta menyelesaikan sistem persamaan tersebut dengan grafik.

Maka, langkah pertama yang harus kamu lakukan adalah membuat grafik persamaan pertama. Hitung titik potong grafik terhadap sumbu x dengan cara memasukkan 0 untuk y:

x + y = 3

x + 0 = 3

x = 3 

Jadi, titik potong x adalah (3, 0). Kemudian, hitung titik potong grafik terhadap sumbu y dengan cara memasukkan 0 untuk x:

x + y = 3

0 + y = 3

y = 3 

Sehingga, titik potong y adalah (0, 3). Selain itu, temukan titik potong lainnya dengan solusi membiarkan x = 1 dengan cara memasukkan 1 untuk x:

x + y = 3

1 + y = 3

1 + y – 1 = 3 – 1

y = 2

Jadi, nilai titik potong yang lain adalah (1, 2). Berdasarkan nilai-nilai titik potong yang sudah kamu hitung sebelumnya, gambarlah garis persamaan linear dua variabel seperti berikut: 

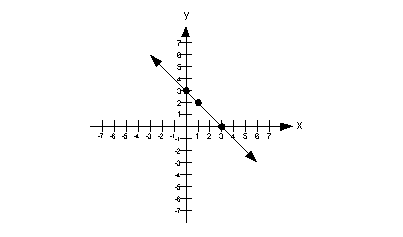
Langkah kedua adalah buatlah grafik persamaan kedua pada sistem koordinat yang sama dengan yang pertama. Hitung titik potong grafik terhadap sumbu x dengan cara memasukkan 0 untuk y:

x – y = 1

x – 0 = 1

x = 1 

Jadi, titik potong x adalah (1, 0). Kemudian, hitung titik potong grafik terhadap sumbu y dengan cara memasukkan 0 untuk x:

x – y = 1

0 – y = 1

– y = 1

y = – 1

Tipsnya, ketika mengalikan suatu nilai dengan -1, maka kebalikannya adalah membagi nilai tersebut dengan -1. Sehingga, titik potong y adalah (0, -1). Setelah itu, temukan titik potong lainnya dengan membiarkan x = 2:

x – y = 1

2 – y = 1

2 – y – 2 = 1 – 2

– y = – 1

y = 1

Jadi, nilai titik potong yang lain adalah (2, 1). Berdasarkan nilai-nilai titik potong yang sudah kamu hitung sebelumnya, gambarlah garis persamaannya seperti berikut:

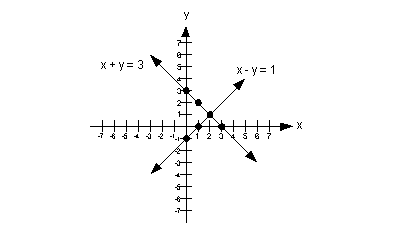
Lalu, langkah yang ketiga adalah menentukan titik potong grafik dengan mencari titik potong antara dua garis. Dalam contoh ini, titik potongnya adalah (2, 1). Periksa apakah pasangan nilai (2, 1) memenuhi kedua persamaan dalam sistem asli. 

Baca Juga : Persamaan Garis Lurus: Pengertian, Sifat, Rumus, dan Soal

Metode Substitusi pada Sistem Persamaan Linear Dua Variabel

Berbeda dari metode grafik, metode substitusi untuk persamaan linear dua variabel adalah pendekatan dalam menyelesaikan sistem persamaan dengan menggantikan salah satu variabel dalam satu persamaan dengan ekspresi dari variabel lainnya.

Adapun langkah-langkah untuk menentukan persamaan linear dengan metode substitusi adalah sebagai berikut:

1. Pertama, susun persamaan linier dalam bentuk umum ax + by = c.
2. Kemudian, pilih salah satu variabel yang akan disubstitusikan.
3. Gantikan variabel yang disubstitusikan dengan ekspresi dari variabel lainnya dalam persamaan lain.
4. Setelah itu, selesaikan persamaan yang diperoleh untuk mencari nilai variabel yang lain.
5. Terakhir, carilah solusi persamaan linear dengan menggunakan nilai variabel yang ditemukan.

Contoh Soal Persamaan Linear Dua Variabel dengan Penyelesaian Metode Subtitusi

Misalkan kamu punya sistem persamaan linear sederhana 3x – 5y = 15; y = 2x + 4. Nah, kamu diminta menyelesaikan sistem persamaan tersebut dengan metode subtitusi.

Maka, langkah pertama yang harus kamu lakukan adalah menyelesaikan satu persamaan untuk salah satu variabel. Perhatikan bagaimana persamaan kedua sudah diselesaikan untuk y.

Langkah kedua adalah tentukan bagaimana kamu bisa beralih ke langkah 1 dalam persamaan yang berbeda. Kemudian, selesaikan untuk sisa variabel dengan cara mengganti 2x + 4 untuk y ke dalam persamaan pertama dan selesaikan untuk x.

3x – 5y = 15

Subtitusikan 2x + 4 untuk y

3x – 5(2x + 4) = 15

3x – 10x – 20 = 15

-7x – 20 = 15

-7x = 15 + 20

x = 35/-7

x = -5

Selanjutnya, selesaikan untuk variabel kedua dengan cara mensubtitusikan -5 untuk x ke persamaan dalam langkah pertaman untuk menemukan nilai y.

y = 2x + 4

y = 2(-5) + 4 = -10 + 4 = -6

Jika sudah menemukan hasil substitusinya, periksa apakah pasangan nilai yang diusulkan, yaitu (-5, -6), memenuhi kedua persamaan dalam sistem asli. Hasilnya menunjukkan bahwa jika nilai tersebut tersubtitusi ke dalam kedua persamaan, maka nilai tersebut memenuhi kriteria tersebut.

Sudah Paham Persamaan Linear Dua Variabel?

Kesimpulannya, persamaan linear dua variabel adalah bentuk persamaan matematika yang melibatkan dua variabel dan memiliki derajat 1. Memahami persamaan linear dua variabel sangat penting karena memiliki banyak aplikasi dalam kehidupan sehari-hari dan berbagai bidang ilmu. Pemahaman tentang persamaan linear dua variabel membantu kamu dalam memecahkan masalah. Kemudian dalam mengambil keputusan yang tepat, dan mempelajari konsep-konsep matematika yang lebih lanjut.