Dalam bidang ilmu Matematika, kamu belajar tentang pertidaksamaan linear, dan juga persamaannya di samping berbagai materi lainnya. Materi ini bisa saja terlihat sulit, lo. Nah, supaya kamu lebih mudah memahaminya, kamu bisa mengikuti ulasannya di bawah ini! Yuk, kita bahas tentang salah satu bidang yang ada di pelajaran matematika ini!
Pertidaksamaan Linear, Apa Itu?
Sederhananya, pertidaksamaan linear adalah salah satu cabang materi di pelajaran matematika yang berasal dari dua kata – pertidaksamaan dan linier. Secara sederhana, artinya mengacu pada kalimat matematis terbuka yang memiliki kandungan berderajat satu serta menggunakan tanda atau simbol yang khas.
Kalau persamaan linier identik dengan simbol (=) atau “sama dengan”, dalam konsep pertidaksamaannya, kamu akan sering bertemu dengan beberapa simbol matematika seperti:
- lebih dari (>),
- kurang dari (<),
- lebih dari atau sama dengan (≥), dan
- kurang dari atau sama dengan (≤).
Pada dasarnya, itulah yang membedakan konsep pertidaksamaan dan persamaan linier.
Lalu, apa arti dari kata linier itu sendiri?
Linier bisa kamu artikan sebagai bentuk aljabar yang memiliki variabel pangkat tertinggi, yaitu satu. Kamu bisa memahami konsep pertidaksamaan tersebut dalam sebuah pernyataan sebagai berikut.
“Siswa dinyatakan lulus ujian jika memperoleh nilai sekurang-kurangnya adalah 80”.
Nah, kalau kamu tulis dengan model matematika, maka bentuknya adalah x ≥ 80. Arti dari model matematika tersebut adalah jika nilai yang kamu peroleh 80 atau lebih, kamu akan lulus.
Lalu, adakah peran pertidaksamaan linear di kehidupan nyata?
Rupanya, konsep yang satu ini juga memiliki banyak peran di berbagai bidang kehidupan dan sering menjadi metode untuk menyelesaikan masalah sehari-hari.
Contohnya, seperti melakukan perkiraan atau ramalan penjualan produk ataupun perhitungan pengeluaran minimal dari pembelian barang.
Perlu kamu ketahui bahwa konsep pertidaksamaan memiliki dua ragam, yaitu jenis yang hanya punya satu variabel, adan yang memiliki dua variabel. Apa bedanya?
Pertidaksamaan Linear Satu Variabel
Pertama-tama, kita akan memahami dulu apa itu sebenarnya kalimat matematika terbuka linear satu variabel.
Jenis pertidaksamaan satu variabel ini hanya memuat satu variabel atau peubah, dengan satu sebagai pangkat tertingginya.
Bagaimana bentuk umumnya? Berikut adalah bentuk umum dari pertidaksamaan linear satu variabel:
ax + b > c, ax + b < c, ax + b ≥ c, ax + b ≤ c
Keterangan:
- (a): koefisien dari variabel (x),
- (x): variabel,
- (b) dan (c): konstanta,
- (<),( >), (≤), (≥) : tanda pertidaksamaan.
Apa saja Sifat Pertidaksamaan linear Satu Variabel?
Kamu perlu mengenal beberapa sifat utama dari jenis pertidaksamaan yang satu ini.
1. Tanda Pertidaksamaan Tidak Berubah Jika Ada Operasi Penjumlahan dan Pengurangan
Operasi penjumlahan atau pun pengurangan di kedua ruas sering kamu gunakan untuk memecahkan masalah pertidaksamaan yang satu ini.
Nah, penjumlahan atau pengurangan yang kamu lakukan pada tiap ruas ini tidak akan mengubah tanda pertidaksamaannya. Berikut adalah contoh soal yang akan membantu kamu memahami sifat ini.
4x + 5 > 21 (kedua ruas kamu kurangi dengan 5)
Jadi, 4x + 5 – 5 > 21 – 5
4x > 16
x > 4
Terkadang, kamu perlu melakukan operasi penjumlahan maupun pengurangan pada tiap ruas dengan tujuan agar kamu bisa menyederhanakan pertidaksamaan tersebut, sehingga lebih mudah untuk menyelesaikannya.
2. Tanda Pertidaksamaan Tidak Berubah Jika Operasi Perkalian Bilangan Positif
Selain penjumlahan dan pengurangan, kamu juga bisa melakukan operasi perkalian dengan bilangan positif di kedua ruas pertidaksamaan linear. Jika kamu melakukan itu, tanda pertidaksamaan tidak berubah
Nah, agar kamu lebih bisa memahaminya, perhatikan contoh di bawah ini.
1/5x < 5, dengan x adalah himpunan bilangan asli
Untuk menyederhanakannya, kamu bisa mengalikan kedua ruas tersebut dengan 5
1/5x . 5 < 5 . 5
x < 25
3. Tanda Pertidaksamaan Berubah Jika Operasi Perkalian Bilangan Negatif
Berbeda dengan perkalian bilangan positif, jika kamu melakukan perkalian bilangan negatif pada kedua ruas pertidaksamaan, maka tandanya pun akan berubah. Amati contoh di bawah ini.
-4x + 6 ≤ 10, kedua ruas dikurangi 6 dahulu
Jadi, -4x + 6 – 6 ≤ 10 – 6
-4x ≤ 4, kemudian kedua ruas dikali -1
4x ≥ -4
Coba kamu perhatikan! Ternyata, tanda pertidaksamaan linear yang awalnya (≤) berubah menjadi (≥).
Contoh Soal pertidaksamaan linear Satu Variabel
Agar kamu bisa menyelami konsep dasar hingga sifat dari jenis pertidaksamaan yang pertama dengan lebih baik, mari membahas contoh soal yang menggunakan konsep ini. Sudah siap?
Contoh Soal
Abdi memiliki 10 butir telur dan Budi memiliki 15 butir telur. Karena satu hal, Abdi dan Budi setuju untuk memberikan telur mereka kepada Deni dengan jumlah yang sama.
Jika sisa telur yang Abdi miliki sekurang-kurangnya dua kali sisa telur Budi, berapa jumlah total telur yang Deni terima?
Pembahasan
Untuk menjawab soal ini, kamu bisa menggunakan konsep pertidaksamaan linear satu variabel. Sebagai contoh, jumlah telur yang Deni terima dari Abdi dan Budi adalah x, sehingga, operasi perhitungannya menjadi seperti berikut ini.
15 – x ≤ 2(10-x)
15 – x ≤ 20 – 2x
-x + 2x ≤ 20 – 15
x ≤ 5
Ini artinya, jumlah telur yang Abdi dan Budi berikan pada Deni masing-masing adalah 5 butir.
Jadi, kita bisa mengetahui bahwa total telur yang Deni peroleh dari Abdi dan Budi adalah 10 butir.
Pertidaksamaan linear Dua Variabel
Kalau kamu ingat kembali, pertidaksamaan linear satu variabel hanya memuat satu variabel atau peubah. Sedangkan, jenis pertidaksamaan dua variabel memiliki dua variabel atau peubah dengan pangkat variabel tertinggi adalah satu.
Di bawah ini adalah bentuk umum dari jenis pertidaksamaan yang kedua ini.
ax + by > c, ax + by < c, ax + by ≥ c, ax + by ≤ c
Keterangan:
- (a): koefisien dari variabel (x),
- (x) dan (y): variabel,
- (b) dan (c): konstanta,
- (<), (>), (≤), (≥) : tanda pertidaksamaan.
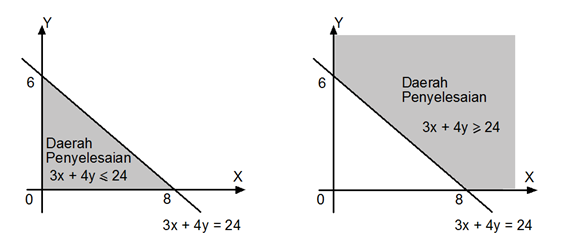
Bentuk pertidaksamaan ini pada dasarnya merupakan daerah pada sistem koordinat kartesius yang dibatasi oleh garis. Nah, daerah itu memiliki nama “daerah penyelesaian”.
Agar kamu bisa memahaminya, yuk perhatikan beberapa contoh yang akan dijelaskan di bawah ini.
1. Metode Uji Titik
Misalnya ada pertidaksamaan linear dua variabel – ax +by ≤ c. Berikut merupakan langkah yang bisa kamu kerjakan
a. Gambar grafik ax + by = c
b. Perhatikan tandanya. Jika (≤) atau (≥), gambar garis pembatas secara penuh. Jika (<) atau (>), gambar garis pembatas secara putus-putus.
c. Kamu sekarang bisa uji titik. Ambil sembarang titik misal (x1,y1) dan (x2,y2). Lalu, masukkan titik tersebut ke dalam pertidaksamaan.
d. Terdapat dua kemungkinan. Jika hasilnya ketidaksamaannya benar, daerah penyelesaian ada di daerah yang memuat titik (x1,y1) dengan garis batas ax + by = c. Jika bernilai salah, daerah penyelesaiannya tidak memuat titik (x1,y1).
2. Perhatikan Tanda Ketidaksamaan
Ada dua hal yang perlu kamu perhatikan pada tanda ketidaksamaan.
a. Pastikan koefisien (x) bernilai positif. JIka tidak, kalikan dengan -1. Ingat, setelah kamu kalikan -1, maka tanda ketidaksamaan akan berubah.
b. Jika sudah positif, perhatikan tandanya.
c. Jika tanda (<) atau (≤), maka daerah penyelesaian ada di kiri garis pembatas
d. Jika tandanya (>) atau (≥), maka daerah penyelesaiannya ada di kanan garis pembatas.
Nah, setelah kamu memahami prinsip pertidaksamaan linear dua variabel, yuk kita langsung lihat contoh soal agar pemahamanmu makin baik.
Baca Juga : Persamaan Linear Dua Variabel: Metode Grafik dan Substitusi
Contoh Soal Pertidaksamaan Linear Dua Variabel
Simak contoh soal berikut ini supaya kamu bisa lebih mengerti konsep pertidaksamaan dengan dua variabel dari penjelasan sebelumnya.
Contoh Soal
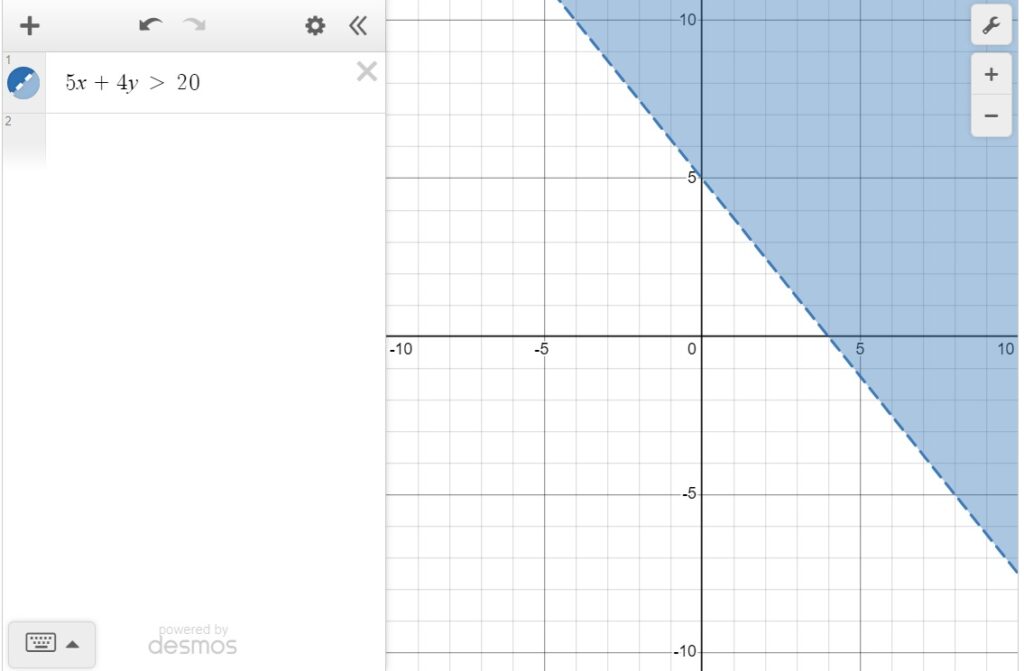
Tentukan daerah penyelesaian pertidaksamaan linear dua variabel ini 5x + 4y > 20
Pembahasan
Jika y = 0, 5x = 20
x = 4
Jika x = 0, 4y = 20
y = 5
Gambar grafik dengan titik (4,5). Lalu, arsir sesuai daerah tanda pertidaksamaan.
Pertidaksamaan linear Mudah, Bukan?
Secara umum, lawan dari persamaan linear ini adalah salah satu materi yang paling sering keluar saat ujian. Oleh sebab itu, pemahaman konsep ini dapat membantumu untuk bisa mengerjakan dan menyelesaikan soal dengan baik.Namun, manfaat pemahaman terhadap konsep matematis ini tidak hanya sebatas nilai di atas kertas. Konsep pertidaksamaan linear sebetulnya bermanfaat di banyak sektor kehidupan, terutama yang berkaitan dengan bisnis.

