Bangun ruang merupakan salah satu konsep matematika yang menjelaskan seputar benda yang bersifat memiliki volume. Oleh sebab itu, jenis-jenis dari bangun ruang ini sangat beragam, mulai dari kubus, balok, hingga limas. Selain itu, penggunaan rumus telah menyesuaikan seperti contohnya rumus bangun ruang limas.
Limas sendiri memiliki pohon keluarga atau jenis-jenis yang cukup beragam, menyesuaikan dengan bentuk alas yang limas miliki. Pada artikel ini, Anda akan belajar lebih mengenai bangun ruang piramida satu ini.
Seputar Limas
Limas merupakan salah satu contoh dari sebuah benda yang memiliki bentuk 3 dimensi dan termasuk dalam materi geometri matematika. Piramida merupakan wujud nyata dari bangun ruang limas tersebut yang memiliki titik puncak dan berselimutkan sisi berbentuk segitiga.
Selain itu, banyak yang menyebut bahwa konsep dari benda 3 dimensi satu ini memiliki kesamaan dengan prisma. Tetapi, hal penting yang harus Anda ketahui untuk dapat membedakan keduanya adalah prisma memiliki atap, sedangkan limas tidak. Atap atau sisi atas sebuah bangun ruang ini yang membedakan keduanya.
Rumus Bangun Ruang Limas
Di samping itu, jenis-jenis limas yang bermacam-macam tersebut memiliki sifat dan rumusnya masing-masing. Ketentuan tersebut telah menyesuaikan sedemikian rupa dengan bentuk dan rumus dari alas bangun ruang tersebut.
Di bawah ini merupakan rumus umum dari bangun ruang limas.
- Luas permukaan: L = LA + LS
- Volume: V = ⅓ × P × L × T
Dengan keterangan tambahan, LA sebagai Luas Alas dan LS sebagai Luas Selimut.
Lantas, bagaimana pembagian dari limas dan rumus bangun ruang limas? Berikut ini adalah penjelasannya.
1. Limas Segitiga
Pembagian jenis limas yang pertama adalah jenis yang paling sering Anda temui, yaitu limas segitiga. Limas ini memiliki bentuk segitiga pada semua sisi dan selimutnya.
Berikut ini adalah ciri dan sifat dari limas segitiga beserta rumusnya.
- Memiliki sisi datar dan sisi tegak berbentuk segitiga.
- Jumlah rusuk sebanyak 6 rusuk.
- Titik sudut berjumlah 4: 3 pada alas dan 1 pada puncak
- Luas permukaan: L = LA + L∆ I + L∆ II + L∆ III
- Volume: V = ⅓ × LA × T
Keterangan:
L = Luas.
L∆ = Luas segitiga
V = Volume
LA = Luas Alas
T = Tinggi
Baca Juga : Rumus Limas Segitiga Beserta Contoh Soal dan Pembahasan
2. Limas Persegi
Sesuai dengan namanya, jenis satu ini memiliki bentuk alas dengan 4 rusuk. Bentuk dari alas limas persegi tidak hanya persegi sama sisi, namun juga termasuk trapesium, belah ketupat, hingga bentuk layang-layang.
Ciri dan sifat dari limas persegi secara umum yaitu sebagai berikut.
- Limas persegi memiliki jumlah sisi n + 1 yaitu 4 sisi tegak + 1 sisi alas, sehingga total sisi limas persegi adalah 5 sisi.
- Rusuk limas persegi berjumlah 2x dari rusuk alas, sehingga jumlah rusuknya sebanyak 8 rusuk.
- Banyaknya titik sudut berjumlah 5 dengan 4 titik sudut pada alas dan 1 titik puncak.
- Sisi alas memiliki bentuk segi empat dengan berbagai bentuk yang memungkinkan.
- 4 sisi tegak memiliki bentuk segitiga.
Lalu, untuk rumus bangun ruang limas persegi adalah sebagai berikut.
- Luas permukaan: L = LA + L∆ I + L∆ II + L∆ III + L∆ IV
- Volume: V = ⅓ × LA × T
Baca Juga : Limas Segi Empat: Sifat, Rumus, Latihan Soal, dan Pembahasan
3. Limas Segi Lima
Selanjutnya adalah bentuk dari limas yang memiliki sisi alas segi lima. Walaupun banyak sisi limas selalu menyesuaikan, tetapi sisi tegak bangun ruang tersebut tetap berbentuk segitiga.
Berikut ini adalah beberapa ciri-ciri dan sifat dari limas segi lima dan juga rumus bangun ruang limas segi lima.
- Jumlah rusuk sebanyak 10 rusuk dari rusuk alas dan rusuk selimut.
- Memiliki 6 titik sudut.
- Bidang diagonal pada limas segi lima berjumlah 5 bidang diagonal dengan bentuk segitiga.
- Luas permukaan: L = LA + L∆ I + L∆ II + L∆ III + L∆ IV + L∆ V
- Volume: V = ⅓ × LA × T
4. Limas Hexagonal atau Limas Segi Enam
Bentuk dari pembagian jenis limas yang selanjutnya adalah limas hexagonal atau biasa disebut dengan limas segi enam. Di bawah ini merupakan ciri dan sifat dari limas hexagonal.
- Memiliki total jumlah rusuk sebanyak 12 rusuk.
- Sisi datar alas memiliki 6 rusuk.
- Titik sudut limas hexagonal sejumlah 7 titik sudut.
- Luas permukaan: L = LA + L∆ I + L∆ II + L∆ III + L∆ IV + L∆ V + L∆ VI
- Volume: V = ⅓ × LA × T
Faktanya, pembagian limas ini tidak hanya sampai yang memiliki segi sebanyak enam saja, namun masih terdapat berbagai macam jenis lainnya. Pembagian tersebut tergantung pada bentuk alas yang mungkin saja dapat berbentuk segi delapan dan seterusnya.
Selain itu, rumus bangun ruang limas akan terus menyesuaikan terutama untuk luas permukaan limas.
Latihan Soal Bangun Ruang Limas
Berikut ini contoh latihan soal limas yang dapat Anda gunakan sebagai alat belajar dan alat memahami dari konsep bangun ruang satu ini.
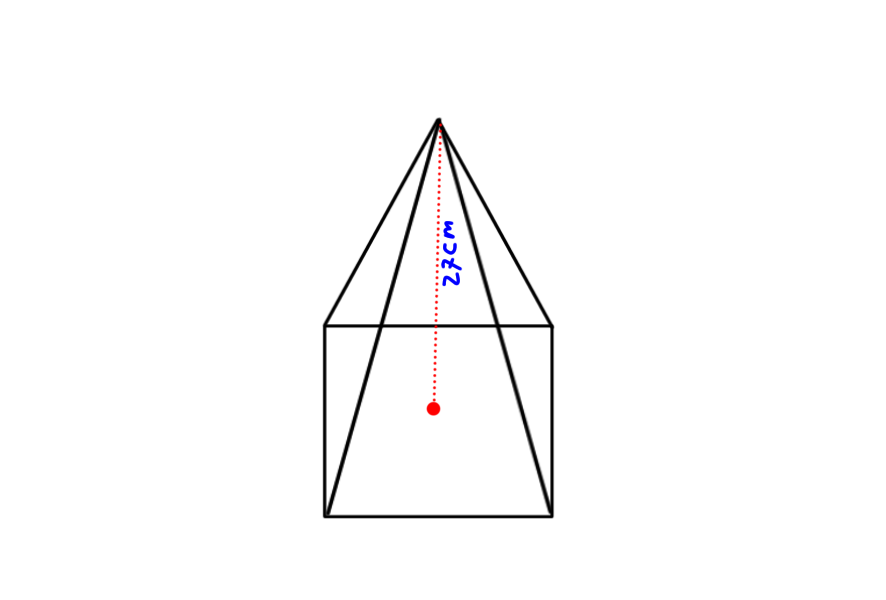
1. Terdapat sebuah limas persegi yang memiliki volume 2.340 cm3 dengan tinggi sepanjang 27 cm. Hitung luas permukaan limas tersebut!
Jawaban.
Diketahui:
V = 2.340 cm3.
T = 27 cm.
Jawab:
V = ⅓ × LA × T
2.340 = ⅓ × LA × 27
LA = 2.340 / 9 = 256
Jadi, sisi persegi dari limas tersebut adalah √256 = 16 cm.
L = LA + total L∆ = (s × s) + (4 × ½ × s × t) = (16 × 16) + (4 × ½ × 16 × 27) = 256 + 854 = 1.120 cm2.
Jadi, total luas permukaan limas persegi tersebut adalah 1.120 cm2.
2. Diketahui sebuah limas segi enam memiliki luas total 180 cm2 dan luas sisi tegak 30 cm2. Berapakah total luas permukaannya?
Jawaban.
L = LA + (6 × luas sisi tegak) = 180 + 180 = 360 cm2.
Jawaban keseluruhannya adalah 360 cm2.
3. Hitung volume dari sebuah limas yang memiliki panjang alas 15 cm dengan lebar 6 cm. Lalu, tinggi limas tersebut adalah 8 cm.
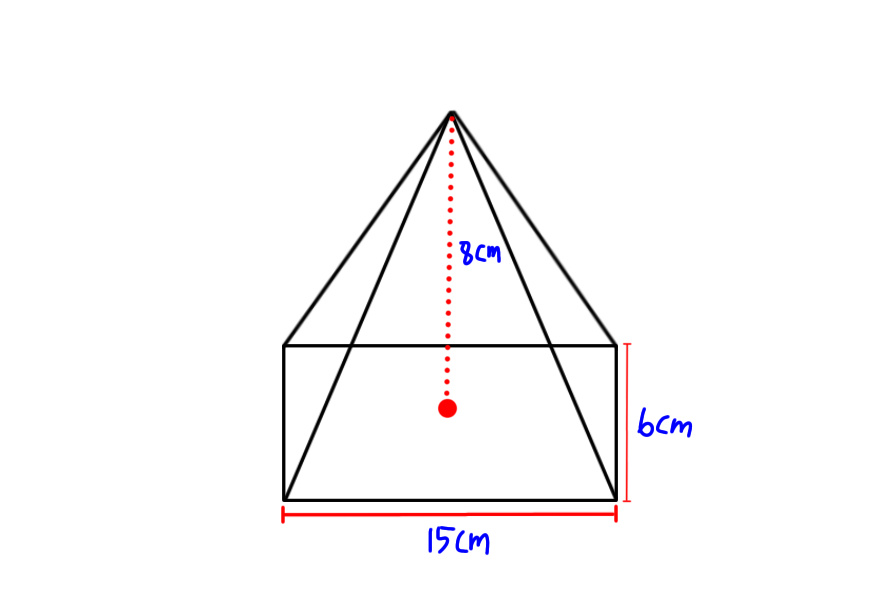
Jawaban.
V = ⅓ × LA × T = ⅓ × (p × l) × T = ⅓ × (15 × 6) × 8 = 240 cm3.
Sudah Paham Mengenai Limas?
Mempelajari matematika memang terkadang terasa sulit dan susah dimengerti. Tetapi, jika Anda belajar dengan cara memahami soal-soal yang memiliki pembahasan ringkas akan terasa lebih mudah. Selain itu, sering membaca dan mencoba menyelesaikan soal-soal latihan akan membantu Anda untuk paham.Di samping itu, Anda tidak perlu menghafal semua rumus dari matematika, namun coba untuk memahami konsep materi tersebut. Seperti contohnya adalah rumus bangun ruang limas yang bergantung pada sisi alas nya. Jika alas limas memiliki lebih dari 4 sisi, maka rumus luas permukaannya dikalikan banyak sisi tersebut.

