Berbicara seputar bangun datar, yang terlintas dalam ingatanmu mungkin hanya persegi, persegi panjang, dan segitiga. Padahal, masih ada lebih banyak jenis bangun datar lainnya, seperti belah ketupat. Setiap jenis bangun ruang memiliki rumus tersendiri untuk menentukan luas dan kelilingnya. Lantas, bagaimana rumus belah ketupat?
Rumus bangun datar umumnya mencakup luas dan keliling. Kamu bisa mempelajari lebih lanjut mengenai cara menghitung luas dan keliling belah ketupat beserta contoh soalnya dalam artikel kali ini.
Rumus Keliling Belah Ketupat
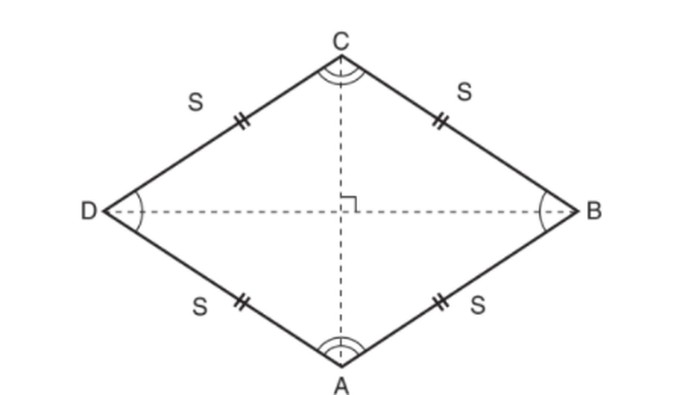
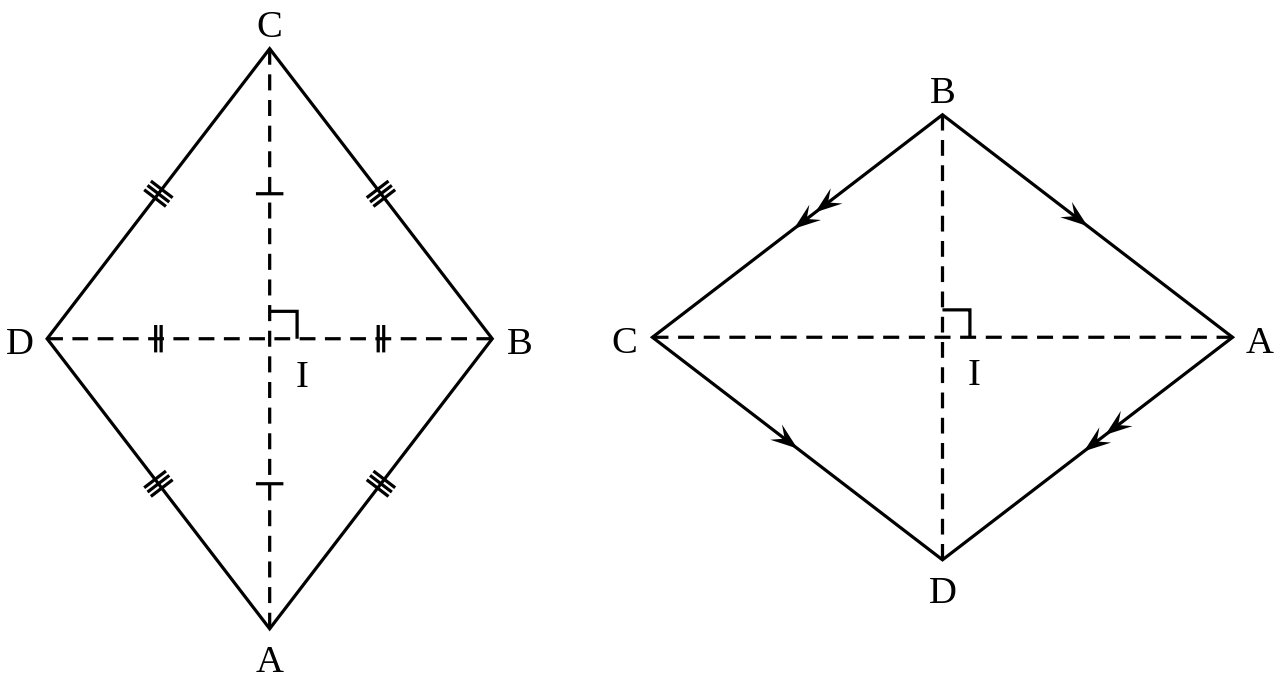
Belah ketupat memiliki empat sisi yang sama panjangnya dan terbentuk dari dua segitiga sama kaki yang kongruen.
Rumus belah ketupat yang pertama, yaitu rumus keliling. Keliling merupakan jumlah semua sisi dari suatu bangun yang dikenal dengan simbol K. Sedangkan simbol untuk panjang sisi adalah “s”. Berikut ini rumusnya:
K = s + s + s + s
K = 4 x s
Rumus Luas Belah Ketupat
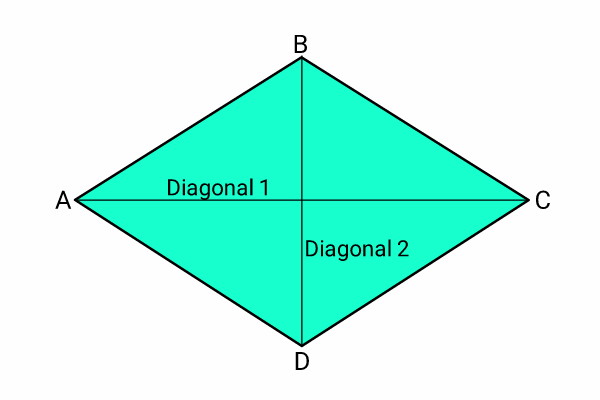
Rumus selanjutnya, yaitu digunakan untuk mengetahui luas bangun datar belah ketupat. Pada dasarnya, luas belah ketupat merupakan setengah dari perkalian panjang diagonalnya.
Diagonal pada belah ketupat terdiri dari dua diagonal yang dikenal dengan simbol d1 dan d2. Berikut rumus lengkapnya:
L = ½ × diagonal 1 × diagonal 2
L = ½ × d1 × d2
Rumus Sisi dan Diagonal Belah Ketupat
Selain rumus luas dan keliling belah ketupat, ada pula rumus untuk mengetahui panjang sisi dan diagonal belah ketupat. Berikut ini masing-masing rumusnya:
Panjang sisi = keliling / 4
Panjang diagonal 1 = (2 x Luas) / diagonal 2
Panjang diagonal 2 = (2 x Luas) / diagonal 1
Unsur-Unsur Belah Ketupat
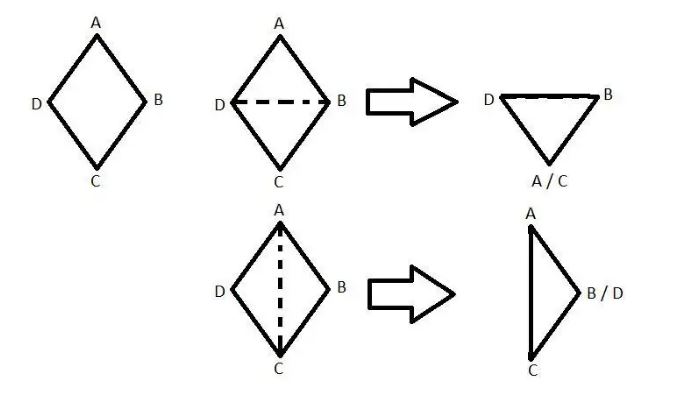
Setelah mengetahui apa saja rumus belah ketupat, penting bagi kamu untuk mengetahui unsur-unsur belah ketupat. Ini bisa menjadi pengetahuan tambahan bagi kamu dalam mengenal bangun datar belah ketupat. Berikut ini beberapa unsur pentingnya:
1. Sisi yang Sama Panjang
Belah ketupat mempunyai empat sisi yang panjangnya sama dan terdiri dari dua pasang sisi yang berhadapan dan saling sejajar. Sisi pada belah ketupat juga tidak saling tegak lurus.
2. Sudut yang Berhadapan yang Sama Besar
Belah ketupat mempunyai empat sudut, dimana sudut yang berhadapan besarnya sama dan terbagi dua oleh diagonal. Dengan kata lain, nilai sudut ∠A = ∠C dan ∠B = ∠D.
3. Sudut yang Berdekatan Saling Berpelurus
Belah ketupat juga mempunyai sudut yang saling berpelurus yaitu sudut yang berdekatan. Sudut yang saling berpelurus apabila dijumlahkan mempunyai jumlah sudut 180 derajat. Sudut ini antara lain ∠A dan ∠B = 180 derajat serta ∠C dan ∠D = 180 derajat.
4. Diagonalnya Tidak Sama Panjang
Unsur belah ketupat selanjutnya, yaitu memiliki dua diagonal yang saling berpotongan tegak lurus. Kedua diagonal ini memiliki panjang yang tidak sama. Oleh sebab itu, AC ≠ BD.
5. Sumbu Simetri
Garis diagonal pada belah ketupat juga menyebabkan bangun datar ini memiliki dua sumbu simetri. Sumbu simetri tersebut adalah garis diagonal 1 dan diagonal 2.
6. Terdiri dari Segitiga Sama Kaki
Apakah kamu menyadari? Bangun datar belah ketupat dapat tersusun dari dua segitiga sama kaki yang kongruen. Pada belah ketupat ABCD, terdapat segitiga sama kaki ABD dan segitiga CBD.
Baca Juga : Rumus Luas Layang-Layang Lengkap dengan Contoh Soalnya
Contoh Soal dan Pembahasan
Berikut beberapa contoh soal dan pembahasannya untuk membantu pemahaman kamu terkait rumus belah ketupat, baik itu luas maupun kelilingnya:
Contoh 1
Diketahui suatu bangun datar belah ketupat ABCD memiliki panjang sisi 13 cm. Berapakah kelilingnya?
Pembahasan:
K = sisi + sisi + sisi + sisi
K = 13 + 13 + 13 + 13 = 52 cm
Jadi, keliling belah ketupat ABCD adalah 52 cm.
Contoh 2
Diketahui sebuah belah ketupat PQRS memiliki panjang diagonal PR 6 cm dan QS 10 cm. Berapakah luas belah ketupat ini?
Pembahasan:
d1 = 6 cm
d2 = 10 cm
L = ½ × d1 × d2
L = ½ × 6 × 10 cm= 30 cm2
Jadi, luas belah ketupat PQRS adalah 30 cm2.
Contoh 3
Sebuah belah ketupat ABCD diketahui mempunyai panjang diagonal AC 12 cm dan BD 16 cm. Hitunglah luas belah ketupat tersebut!
Pembahasan:
d1 = 12 cm
d2 = 16 cm
L = ½ × d1 × d2
L = ½ × 12 × 16 cm= 96 cm2
Jadi, luas belah ketupat ABCD adalah 96 cm2.
Contoh 4
Diketahui sebuah bangun belah ketupat DEFG dengan panjang sisi 15 m. Tentukan keliling bangun tersebut!
Pembahasan:
K = sisi + sisi + sisi + sisi
K = 15 + 15 + 15 + 15 = 60 m
Jadi, keliling belah ketupat DEFG adalah 60 m.
Contoh 5
Terdapat sebidang tanah yang berbentuk belah ketupat dengan masing-masing diagonal panjangnya 12 m dan 10 m. Tentukan luas tanah tersebut!
Pembahasan:
L = ½ x diagonal 1 x diagonal 2
L = ½ x 12 x 10 m= ½ x 120 = 60 m2
Maka, luas sebidang tanah berbentuk belah ketupat tersebut adalah 60 m2.
Contoh 6
Sebuah bangun datar belah ketupat mempunyai keliling 24 cm. Berapakah panjang sisi bangun datar tersebut?
Pembahasan:
Panjang sisi = keliling / 4
Panjang sisi = 24 / 4 = 6 cm
Maka, panjang masing-masing sisi bangun datar di atas adalah 6 cm.
Contoh 7
Sebuah belah ketupat mempunyai luas 24 cm2. Salah satu diagonalnya memiliki panjang 4 cm. Berapakah panjang diagonal lainnya?
Pembahasan:
Panjang diagonal 2 = (2 × L) / d1
d2 = (2 × 24) / 4 cm= 48 / 4 cm = 12 cm
Maka, panjang diagonal lainnya pada bangun datar di atas adalah 12 cm.
Contoh 8
Arga berlari mengelilingi lapangan berbentuk belah ketupat yang memiliki ukuran sisi 20 m. Apabila Arga mengelilingi lapangan sebanyak 10 kali, berapakah jarak lintasan yang ditempuh Arga?
Pembahasan:
Keliling lapangan = 4 × sisi
K = 4 × 20 m= 80 m
Maka, jarak lintasan = keliling lapangan × jumlah putaran
Jarak lintasan = 80 × 10 = 800 m
Jadi, jarak lintasan yang ditempuh Arga adalah 800 m.
Contoh 9
Sebuah taman berbentuk belah ketupat memiliki sisi berukuran 5 m. Apabila di sekeliling taman tersebut akan dipasang lampu dengan jarak 2 m, berapakah jumlah lampu yang dibutuhkan?
Pembahasan:
Keliling taman = 4 × sisi= 4 × 5 = 20 m
Jumlah lampu = keliling taman / jarak lampu= 20 / 2 m = 10
Jadi, jumlah lampu yang dibutuhkan untuk taman tersebut adalah 10 buah.
Baca Juga : Memahami Ciri dan Sifat Bangun Datar serta Pembahasannya
Sudah Lebih Memahami Rumus Belah Ketupat?
Secara keseluruhan, belah ketupat mempunyai beberapa rumus untuk menghitung luas, keliling, panjang sisi, dan diagonalnya. Ada pula unsur-unsur yang menyusun bangun datar belah ketupat.
Kamu pun bisa mempelajari contoh soal serta pembahasannya seperti yang telah kami paparkan sebelumnya, agar lebih mudah dalam mengaplikasikan berbagai rumusnya.