Salah satu jenis perhitungan matriks yang paling familiar dalam pelajaran matematika adalah matriks invers. Secara spesifik, keberadaan rumus matriks invers menjadi salah satu konsep penting dalam aljabar linier yang memiliki berbagai aplikasi dalam matematika, ilmu pengetahuan, teknik, dan berbagai bidang lainnya.
Lantas, bagaimana rumus tersebut bisa kita gunakan dalam mempelajari ilmu matematika kompleks? Dalam artikel ini, kita akan menjelajahi apa itu matriks invers, bagaimana cara menghitungnya, serta beberapa contoh soal sekaligus pembahasan yang harus Anda pelajari.
Apa Itu Matriks Invers?
Pada dasarnya, istilah invers memiliki arti “kebalikan”, sehingga matriks invers merujuk pada konsep kebalikan dari sebuah matriks. Jika suatu matriks dikalikan dengan invers matriksnya, maka akan menghasilkan rumus matriks identitas.
Seperti yang Anda ketahui, setiap pelajaran matematika pasti memiliki notasi yang berbeda-beda. Nah, notasi untuk melambangkan rumus matriks invers adalah dengan pangkat -1 (A-1). Harapannya, lambang tersebut bisa memudahkan Anda untuk mengenali suatu invers, khususnya pada matriks.
Namun, Anda perlu tahu bahwasannya tidak semua bilangan matriks memiliki invers. Jika suatu matriks tidak memiliki invers, maka matriks tersebut disebut dengan matriks non singular, yaitu suatu matriks yang memiliki nilai determinan tidak sama dengan nol. Berikut ini rumusnya:
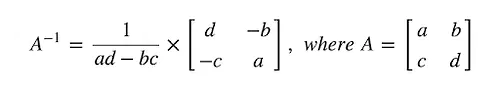
Sedangkan apabila suatu matriks memiliki nilai determinan sama dengan nol, maka matriks tersebut disebut sebagai matriks singular. Penggambaran rumus matriks singular dapat Anda lihat di bawah ini:

Ada beberapa syarat dalam memahami konsep matriks invers ini, di antaranya adalah sebagai berikut:
- Suatu matriks berbentuk bujur sangkar.
- Jika determinan A tidak sama dengan nol, maka matriks memiliki invers. Sedangkan apabila determinan A nilainya sama dengan nol, maka matriks tersebut tidak memiliki invers.
Salah satu kegunaan perhitungan materi ini adalah untuk membantu penyelesaian soal matematika dalam suatu fungsi dan matriks. Dalam konteks rumus matriks invers, sebagian orang berpandangan bahwa matriks invers berhubungan dengan fungsi invers. Padahal, keduanya memiliki definisi yang berbeda.
Ketika memahami persoalan matriks invers, maka Anda perlu mengenali terlebih dahulu apa itu determinan. Sebab, keduanya saling berkaitan satu sama lain.
Determinan matriks merupakan unsur-unsur yang ada pada matriks persegi. Untuk menghitung rumusnya, Anda bisa mengurangkan hasil perkalian pada diagonal utama dan diagonal kedua.
Sifat-Sifat Matriks Invers
Sebelum memasuki cara menyelesaikan soal matriks, pahami dulu sifat-sifat matriks A, B, dan C serta I adalah matriks identitas. Berikut ini sifat-sifatnya:
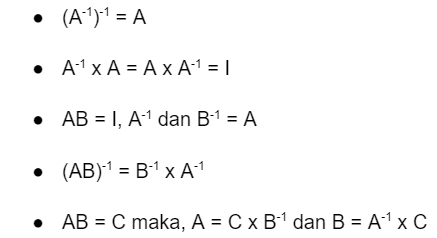
Cara Menyelesaikan Rumus Matriks Invers
Dalam perhitungan matriks invers, terdapat dua aturan yang bisa digunakan untuk bisa menyelesaikan contoh soalnya. Aturan tersebut berhubungan dengan ordo dalam suatu matriks. Berikut ini penjelasan aturannya:
1. Invers Matriks Ordo 2×2
Aturan yang pertama adalah dengan menggunakan rumus determinan lantaran matriks yang digunakan merupakan ordo persegi. Oleh karena itu, cara penyelesaiannya adalah menggunakan rumus berikut ini:
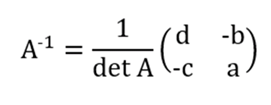
Rumus tersebut berasal dari konsep berikut:
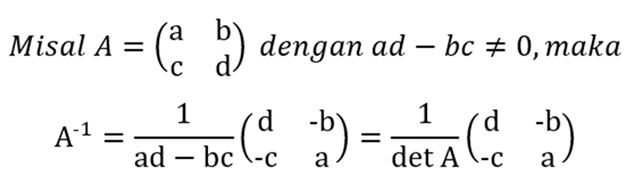
Anda bisa menghitungnya menggunakan rumus matriks invers dengan langkah yang sesuai. Langkah-langkahnya adalah Anda perlu menukarkan elemen pada diagonal utama dan diagonal kedua, lalu memberikan tanda negatif untuk elemen lainnya. Kemudian, Anda bisa langsung mengoperasikannya.
Rumus ini berfungsi dalam menghitung sistem persamaan linier. Jadi, jika Anda mendapatkan soal persamaan linier pada aljabar, maka gunakanlah matriks invers untuk memecahkan soalnya.
2. Invers Matriks Ordo 3×3
Selanjutnya adalah matriks yang berordo 3×3. Rumus yang kedua ini dapat Anda selesaikan dengan dua metode, yaitu metode adjoin dan transformasi baris elementer. Anda bisa pahami masing-masing penjelasannya di bawah ini:
a. Metode Adjoin
Metode adjoin merupakan metode perhitungan matriks dengan menggunakan kofaktor transpose matriks, sehingga elemen-elemen yang ada di dalamnya merupakan suatu kofaktor dari transpose matriks. Sebelum membahas mengenai adjoin, Anda harus paham dulu terkait kofaktor matriks.
Adapun ilustrasi rumus matriks invers dengan metode adjoin adalah sebagai berikut:
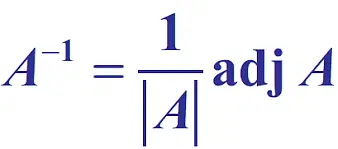
Supaya Anda mudah memahami rumus di atas, perhatikan contoh soal dan penyelesaiannya di bawah ini:
Diketahui pola matriks A seperti ini:
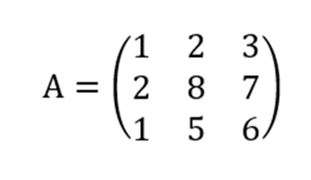
Langkah pertama, cari determinan dari matriks A dengan metode Sarrus:
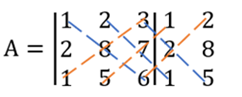
detA = (1 x 8 x 6) + (2 x 7 x 1) + (3 x 2 x 5) – (1 x 8 x 3) + (5 x 7 x 1) + (6 x 2 x 2)
detA = 48 + 14 + 30 – 24 – 35 – 24 = 9
Langkah kedua, tentukan adjoin matriks A dengan mencari kofaktornya terlebih dahulu.
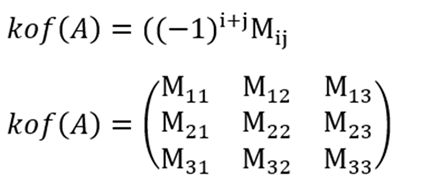
Dari rumus tersebut, Anda perlu mengetahui bilangan yang berada dalam elemen-elemen di dalamnya. Kofaktor dalam matriks A dapat ditentukan melalui teori seperti di bawah ini:
- Menghilangkan elemen baris dan kolom pertama.
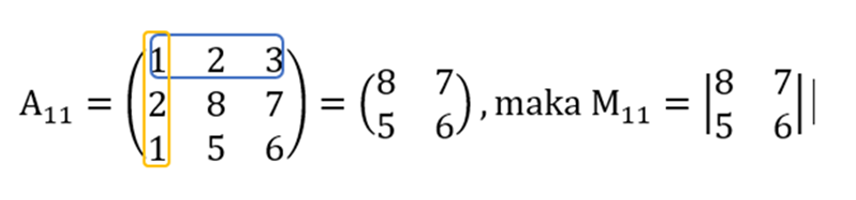
- Menghilangkan baris pertama dan kolom kedua.
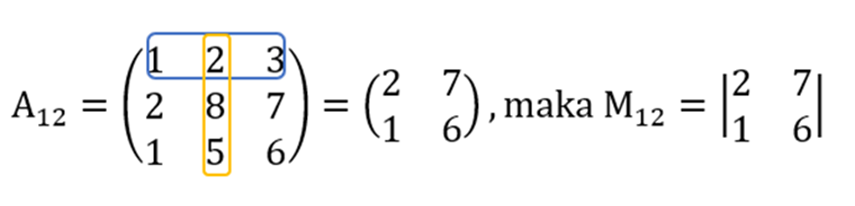
- Menhapus elemen baris pertama dan kolom ketiga.
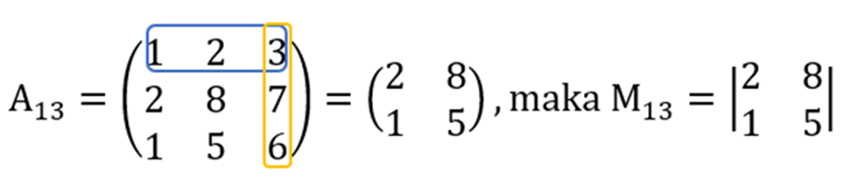
- Menghapus baris kedua dan kolom pertama.
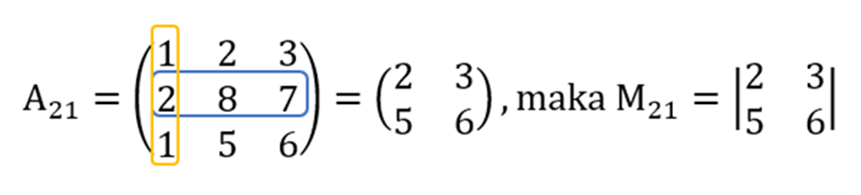
- Menghilangkan baris kedua dan kolom kedua.
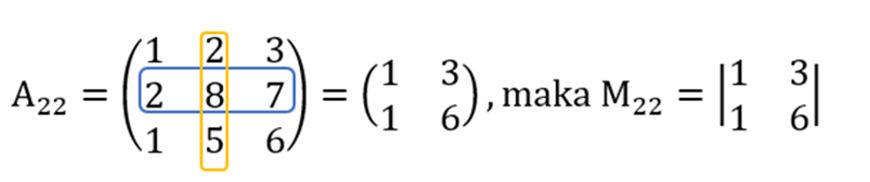
- Menghilangkan baris kedua dan kolom ketiga.
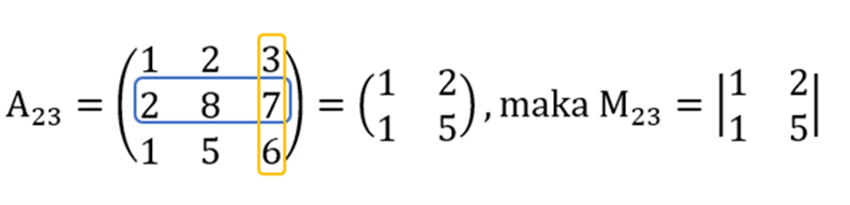
- Menghilangkan baris ketiga dan kolom pertama.
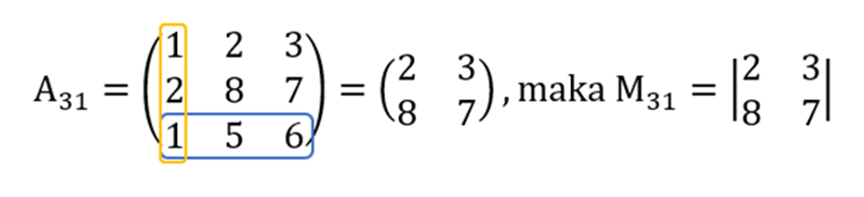
- Menghapus baris ketiga dan kolom kedua.
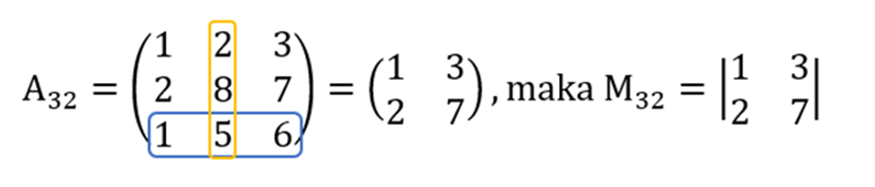
- Menghapus baris ketiga dan kolom ketiga.
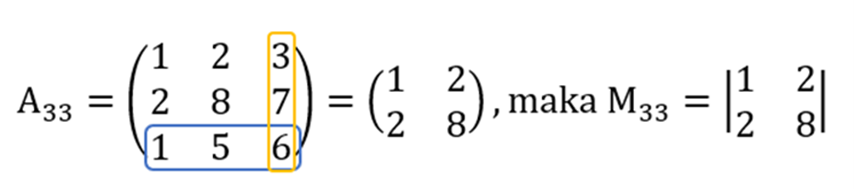
Jadi, hasil dari kofaktor matriks A adalah:
Selanjutnya, tentukan adjoin dan invers matriks A melalui rumus matriks invers berikut ini:

b. Metode Transformasi Baris Elementer
Jika Anda ingin menyelesaikan studi kasus matriks invers menggunakan metode transformator, maka pahami langkah-langkah berikut ini:
- Bentuklah matriks dengan model (An | In), di mana In merupakan matriks yang memiliki ordo n.
- Lalu, transformasikan matriks ke bentuk (In | Bn) menggunakan transformasi baris.
- Hasil yang diperoleh merupakan invers matriks An, yaitu Bn.
Nah, barangkali Anda masih bingung dengan penjelasan di atas, yuk langsung ikuti tahapan-tahapan contoh berikut ini:
Diketahui, matriks A seperti berikut
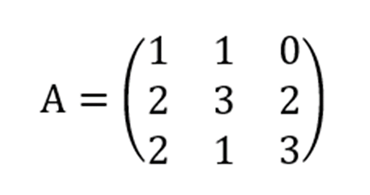
Sesuai petunjuk di atas, Anda perlu mengubah matriks A menjadi matriks (A3 | I3).
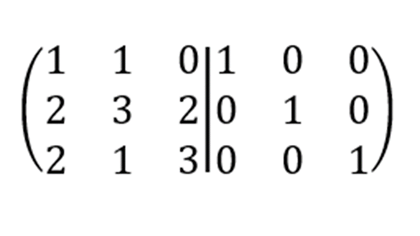
Kemudian, transformasikan matriks (A3 | I3) menjadi (I3 | A3). Langkah-langkah tranformasinya adalah seperti berikut ini:
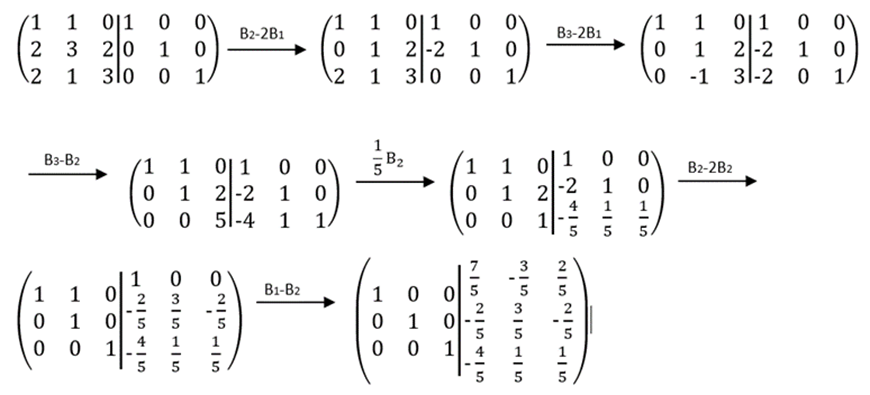
Keterangan:
- B2-2B1 = Mengurangi elemen baris kedua dengan hasil dua kali elemen baris pertama.
- B3-2B1 = Mengurangi elemen baris ketiga dengan dua kali hasil elemen baris ke satu.
- B3-B2 = Menjumlahkan elemen baris ketiga dengan baris kedua.
- 1/5B3 = Mengalikan elemen baris ketiga dengan ⅕.
- B2-2B3 = Elemen baris kedua dikurangi dua kali elemen baris ketiga.
- B1-B2 = Elemen baris pertama dikurangi elemen baris kedua.
Jadi, hasil akhir dalam menyelesaikan rumus matriks invers dengan menggunakan metode transformasi baris elementer adalah:
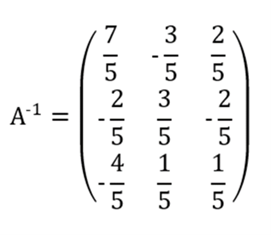
Contoh Soal dan Pembahasan Rumus Matriks Invers
Berdasarkan pemaparan penjelasan di atas, maka kini saatnya berlatih soal-soal agar pemahaman Anda semakin mahir dalam persoalan invers matriks. Berikut ini contoh-contoh soalnya:
1. Soal Pertama
Diketahui matriks
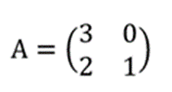
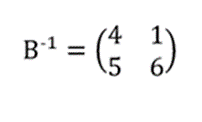
Tentukan nilai (A-1 x B)-1!
Penyelesaian:
Dalam menyelesaikan soal tersebut, Anda bisa menggunakan rumus matriks invers sesuai dengan sifat di atas. Begini caranya:
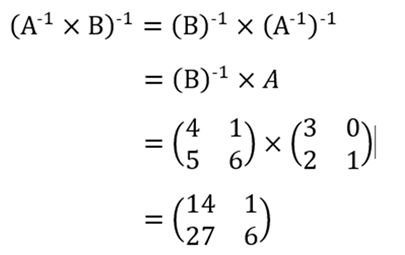
2. Soal Kedua
Diketahui terdapat duaa matriks A dan B seperti berikut:
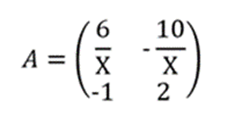
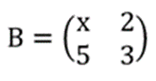
Jika AT = B-1, maka nilai 2x adalah…
Jawab:
Pertama-tama, tentukan transpose dari matriks A terlebih dahulu:
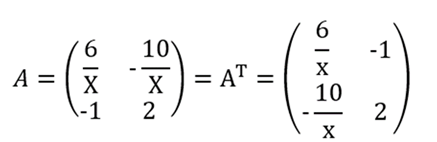
Kemudian, tentukan invers matriks B:
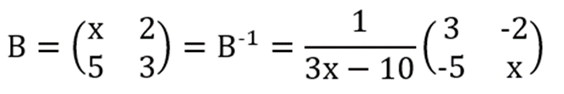
Dengan demikian, berdasarkan rumus pada soal, maka:
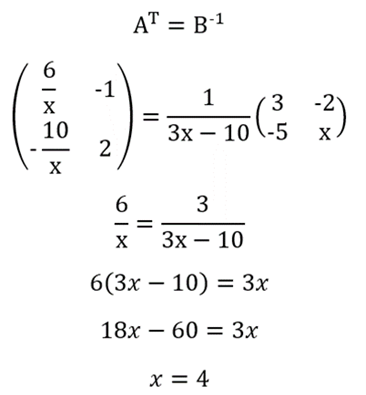
Jadi, nilai dari 2x adalah 2(4) = 8
Baca Juga : Rumus Matriks Transpose Lengkap dengan Contoh Soalnya
Sudah Paham dengan Rumus Matriks Invers?
Berdasarkan penjelasan sebelumnya, Anda sudah tahu bagaimana menyelesaikan soal-soal menggunakan rumus matriks invers. Sebenarnya, mempelajari invers matriks cukup mudah, asal Anda mengetahui sifat-sifat dan pola matriksnya.
Selain itu, terkadang orang-orang sering terbalik dalam menilai fungsi invers dan invers matriks, padahal keduanya memiliki definisi yang berbeda. Fungsi invers merupakan suatu fungsi matematika yang berkebalikan dengan fungsi awalnya, sedangkan invers matriks merupakan lawan dari sesuatu.
Dalam definisinya, mungkin Anda akan menemukan beberapa kesamaan terkait “kebalikan”. Pada faktanya, teori fungsi invers dan matriks invers memiliki rumus dan konsep pengerjaan yang berbeda.

