Matriks adalah komponen penting dalam matematika, ilmu komputer, fisika, dan banyak bidang lainnya. Nah, dalam aljabar linier, rumus matriks transpose merupakan salah satu metode untuk menyelesaikan transformasi matriks.
Pada artikel kali ini, kita akan membahas mengenai pengertian, sifat, rumus matriks transpose, dan cara menyelesaikan contoh soalnya. Yuk, belajar bersama melalui artikel ini!
Apa Itu Matriks Transpose?
Matriks transpose merupakan salah satu bagian dari jenis operasi matriks pada ilmu matematika. Transformasi matriks ini terjadi dengan penukaran antara elemen baris menjadi elemen kolom, begitu pun sebaliknya.
Seperti yang Anda sudah tahu sebelumnya, matriks merupakan susunan bilangan yang tersusun dalam suatu baris dan kolom. Bilangan yang berada pada susunan baris dan kolom disebut sebagai elemen baris dan elemen kolom.
Biasanya, elemen-elemen tersebut berada di dalam suatu tanda kurung kurawal. Nah, transpos matriks tidak memiliki rumus tertentu, hanya saja notasi yang digunakan sebagai penanda rumus matriks transpose adalah AT (A pangkat T).
Walaupun materi ini tergolong mudah, namun Anda harus berhati-hati dalam menyelesaikannya. Sebab, ada beberapa aturan terkait model matriks untuk dijadikan transformasi.
Jika matriks berbentuk persegi, maka tidak ada perubahan ordo dalam penukaran elemen. Aturan tersebut berlaku karena matriks persegi memiliki ordo 2×2 atau 3×3, di mana ukuran baris dan kolomnya tetap. Jadi, matriks persegi memiliki transpos matriks dengan ordo yang sama.
Berbeda halnya ketika terdapat matriks dengan ordo 3×1, 2×3, dan 1×2, maka perubahan ordo akan berlaku dalam penukaran elemen. Sehingga, matriks berubah menjadi ordo 1×3, 3×2, dan 2×1. Berikut ini terdapat ilustrasi cara melakukan matriks transpos:
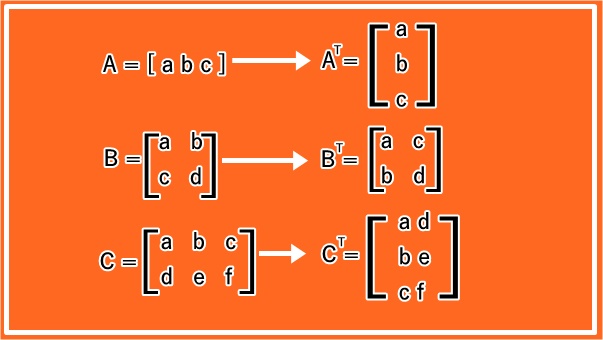
Sebagai contoh soal, diketahui matriks A, B, dan C memiliki persamaan sebagai berikut:
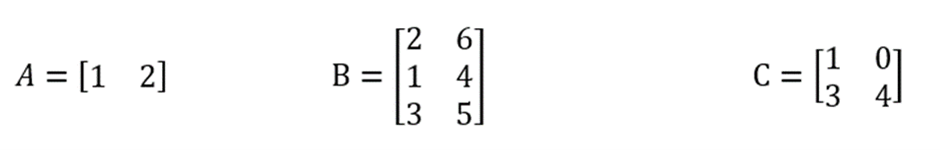
Terlihat bahwa matriks A memiliki ordo 1×2, B berordo 3×2, sedangkan matriks C berordo 2×2. Matriks C merupakan matriks yang berbentuk persegi. Sehingga, pahami pembahasan berikut ini:
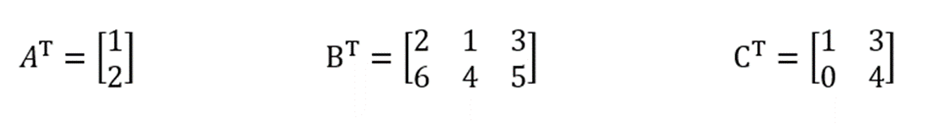
Ketiga matriks transpos di atas telah bertukar posisi yang semula berupa elemen baris menjadi elemen kolom. Kondisi tersebut menyebabkan ordo setiap matriks berubah. Matriks A berordo 2×1, B memiliki ordo 2×3, dan matriks C ordonya tetap 2×2.
Oleh karena itu, matriks persegi tidak memiliki perubahan rumus matriks transpose secara signifikan, hanya penggantian angka pada elemen baris dan kolom. Mudah, bukan?
Sifat-Sifat Rumus Matriks Transpose
Matriks transpos memiliki beberapa sifat untuk memudahkan Anda dalam menyelesaikan operasi perhitungan. Berikut ini penjelasan sifat-sifatnya:
1. Transformasi Matriks Transpos
Sifat pertama adalah transformasi matriks transpos. Artinya, suatu bilangan matriks yang mengalami transformasi sebanyak dua kali akan menghasilkan matriks awal. Coba pahami ilustrasi berikut:
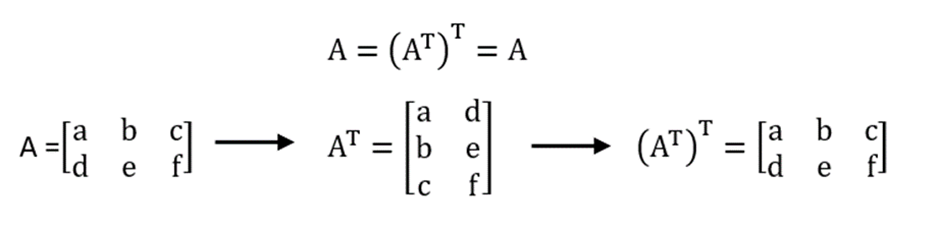
2. Penjumlahan Transpos Matriks
Selanjutnya adalah operasi penjumlahan dua bilangan matriks A dan B. Kasus seperti ini bisa Anda selesaikan dengan mudah, karena hasil akhirnya merupakan matriks A dan B itu sendiri. Berikut rumus matriks transpose dengan operasi penjumlahan:
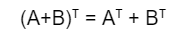
Agar tampak nyata, di bawah ini terdapat pembuktian dari rumus di atas:
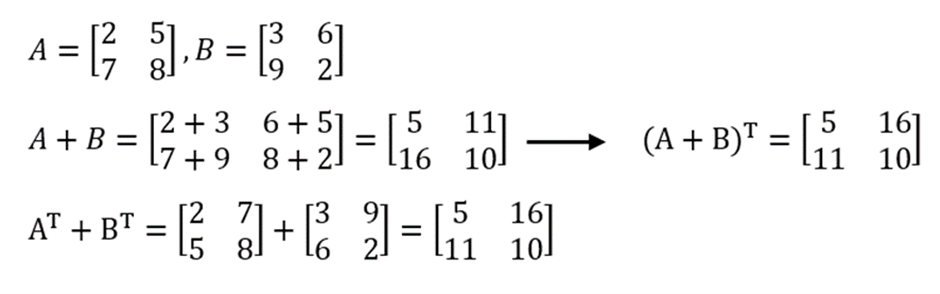
3. Pengurangan Transpose Matriks
Sifat ketiga ini merupakan bagian dari sifat sebelumnya. Cara penyelesaian dan rumusnya pun sama dengan penjumlahan. Berikut aturannya:
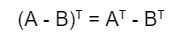
Berikut penjabaran dari rumus tersebut:
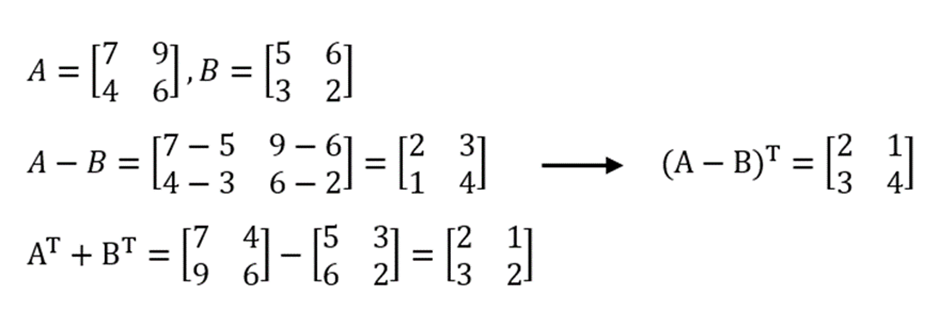
4. Perkalian dengan Konstanta
Jika Anda mengalikan bilangan matriks dengan konstanta lalu ditransformasikan, maka hasilnya adalah konstanta dan matriks transpose itu sendiri. Berikut ini aturannya:
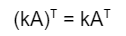
Pembuktian dari rumus di atas adalah seperti berikut:

5. Sifat Perkalian Transpose
Sifat yang terakhir adalah berkaitan dengan operasi perkalian. Jika Anda menemukan perkalian dua matriks yang ditransformasikan, maka hasil akhirnya aadalah sama dengan hasil kali transpose kedua matriks tersebut. Berikut ini aturannya:
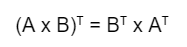
Anda bisa melihat operasi penyelesaian dari rumus matriks transpose tersebut di bawah ini:
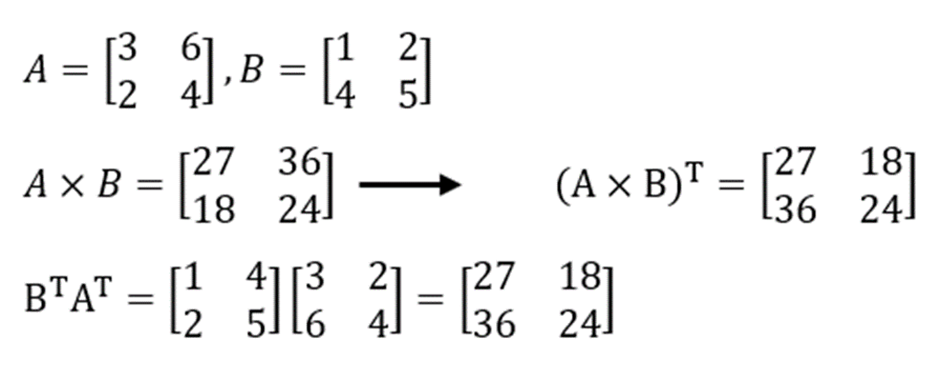
Contoh Soal Beserta Penjelasan Rumus Matriks Transpose
Nah, untuk melatih pemahaman Anda yang sedang belajar rumus matriks transpose, Anda bisa mempelajari beberapa tipe soal dan jawabannya di bawah ini:
1. Contoh Soal Pertama
Carilah hasil matriks transpose dari matriks A, B, dan C, di bawah ini:
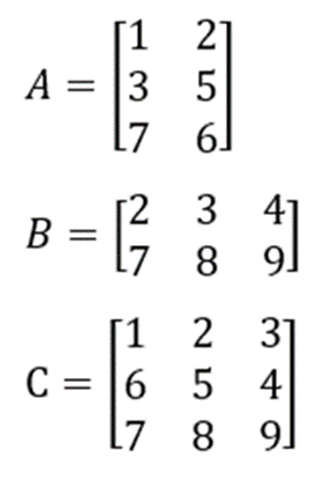
Penyelesaian:
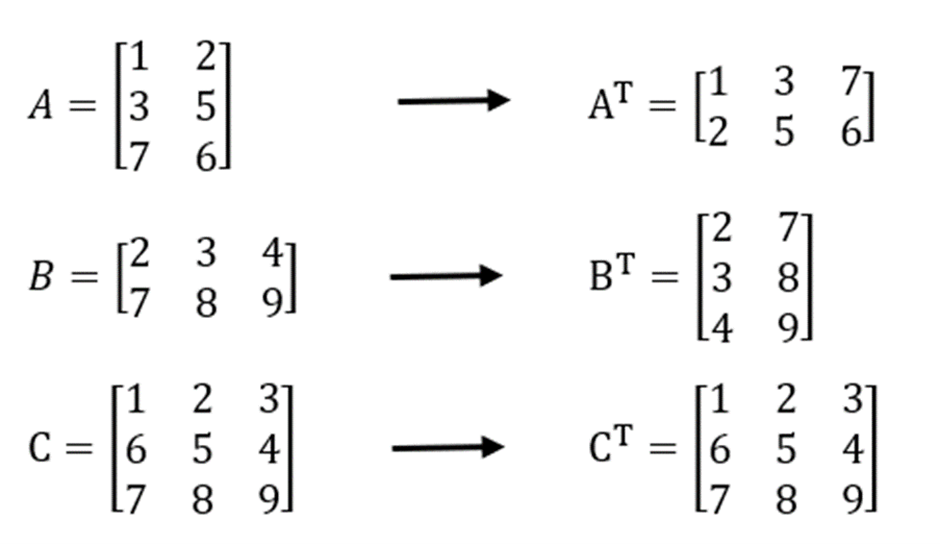
2. Contoh Soal Kedua
Jika diketahui matriks A, B, dan C yang mana ketiganya memenuhi A+B=CT, maka berapakah hasil 2x+3y?
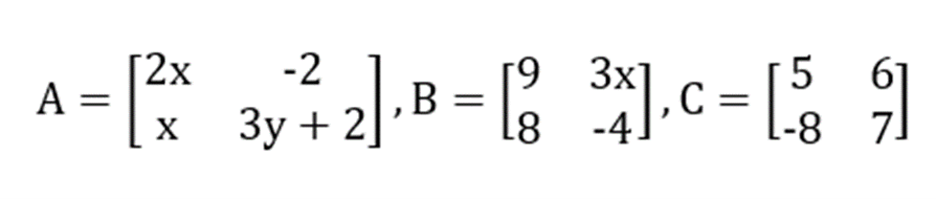
Penyelesaian:
- Langkah pertama untuk menyelesaikan soal seperti di atas adalah dengan mengoperasikan persamaan matriks sesuai dengan rumus matriks transpose yang tertera pada soal.
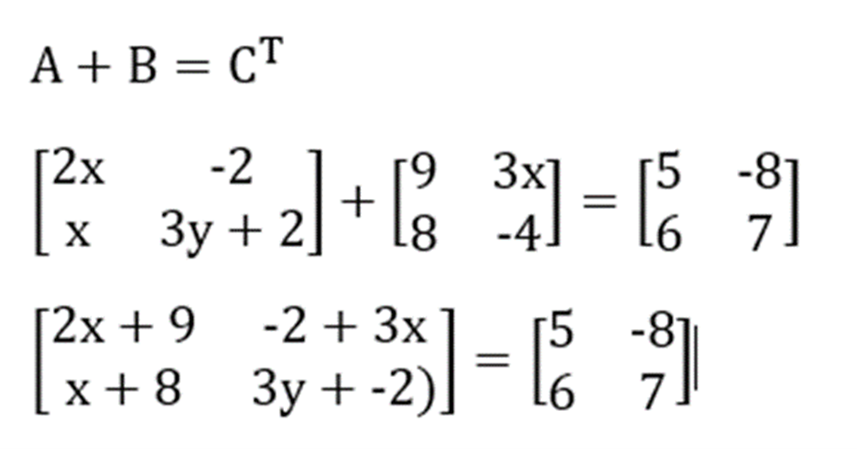
- Kemudian, carilah nilai x dan y seperti berikut ini:
2x + 9 = 5
2x = 9 – 5 = 4
x = 2
3y + (-2) = 7
3y = 7 + 2 = 9
y = 3
- Jadi, hasil operasi penjumlahan dari 2x+3y adalah
2x + 3y = 2(2) + 3(3) = 4 + 9 = 13
3. Contoh Soal Ketiga
Terdapat tiga buah matriks seperti berikut:
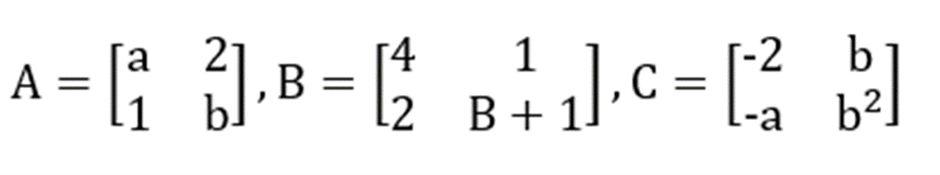
Jika A x BT – C = dengan BT adalah hasil rumus matriks transpose matriks B, maka hitunglah nilai a dan b!
Penyelesaian:
- Penyelesaian pertama adalah dengan mencari transpos matriks B

- Kemudian, carilah nilai a dan b menggunakan rumus matriks transpose sebagai berikut:
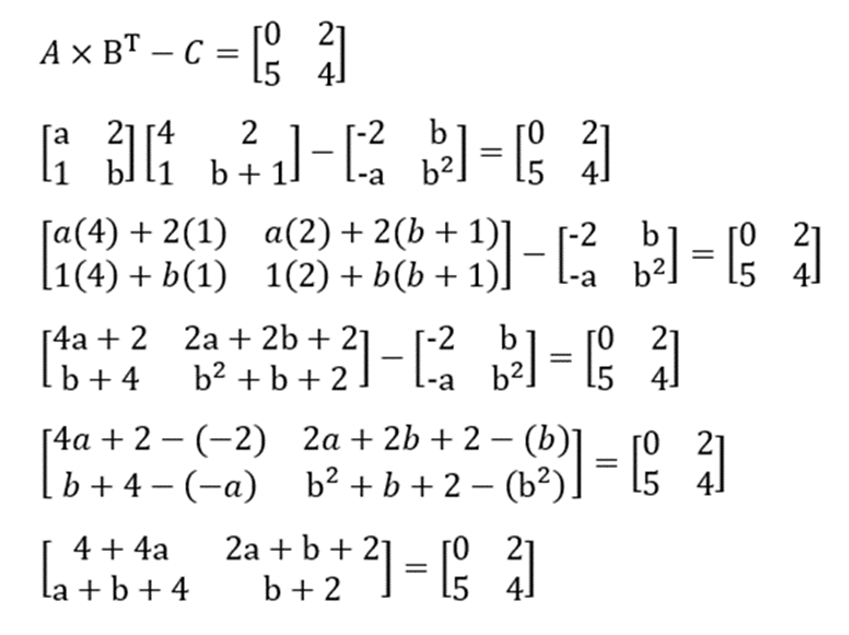
Dengan demikian, Anda bisa menghitung nilai a dan b melalui persamaan di bawah ini:
| 4 + 4a = 04a = -4a = -1 | b + 2 = 4b = 4 – 2 = 2 |
Manfaat Mempelajari Rumus Matriks Transpose

Pada dasarnya, belajar materi transpos matriks bukan hanya sebagai untuk ilmu matematika. Akan tetapi, materi ini juga bisa diaplikasikan dalam bidang teknik dan ilmu komputer. Berikut ini beberapa manfaat yang bisa Anda ambil dalam belajar rumus matriks transpose:
1. Memudahkan Menghitung Matriks dan Persamaan Linier
Manfaat yang pertama adalah dapat memudahkan Anda untuk melakukan perhitungan matriks dan sistem persamaan linier. Penyelesaian ini biasa digunakan dalam kasus numerik dan algoritma.
2. Mengolah Citra dan Grafik dalam Ilmu Komputer
Selain matematis, matriks transpos juga berfungsi untuk membantu para ahli komputer dalam memutar citra dan grafik pada objek. Contohnya adalah ketika akan memutar gambar sebesar 90o, maka Anda bisa menggunakan operasi rumus matriks transpose terlebih dahulu.
3. Analisis Data
Manfaat yang ketiga adalah dapat memudahkan Anda dalam melakukan analisis data dengan bantuan penukaran data pada baris dan kolom. Biasanya, cara ini bermanfaat dalam melakukan analisis statistik dan visualisasi data.
4. Pengkodean dan Kriptografi
Selanjutnya, teori ini juga berguna untuk menjaga keamanan data dan informasi melalui kode matriks transpose. Sehingga, program akan sulit untuk dirusak oleh pihak tidak berwenang.
5. Aljabar Linier
Manfaat yang terakhir ini merupakan salah satu konsep dasar dalam aljabar. Sebab, banyak teori yang melibatkan materi ini dalam menyelesaikan konsep aljabar.
Baca Juga : Transpose Matriks: Pengertian, Ciri, Jenis, dan Contoh Soal
Sudah Paham Cara Menghitung Rumus Matriks Transpose?
Demikian penjelasan singkat terkait pengertian, sifat, dan cara perhitungan menggunakan rumus matriks transpose. Pada dasarnya, operasi matriks ini merupakan perhitungan matematika yang melibatkan penukaran baris menjadi kolom, begitu pun sebaliknya.
Hasil akhir dari penyelesaian operasi matematika ini akan memiliki dimensi yang berlawanan dengan matriks asal. Untuk memudahkan proses belajar Anda, ada baiknya mulailah dengan matriks sederhana, seperti matriks persegi 2×2, dan aplikasikan rumus transpos untuk matriks ini.
Setelah Anda merasa nyaman dengan contoh-contoh sederhana, lanjutkan dengan matriks berukuran lebih besar. Pahami bahwa rumus transpos akan berlaku untuk matriks berukuran m x n, bukan hanya 2×2.

