Teorema pythagoras adalah dasar teori hubungan antara tiga sisi segitiga siku-siku. Selain itu, materi ini tentunya memiliki sejarah yang menarik untuk dipelajari. Pada artikel ini, kita akan mempelajari sejarah, rumus teorema pythagoras, hingga contoh soal serta pembahasannya. Mari pelajari bersama!
Sejarah Teorema Pythagoras
Rumus teorema phytagoras merupakan salah satu prinsip dasar pada geometri matematika yang tidak lain merupakan penemuan dari seorang ahli matematika Yunani kuno, bernama Pythagoras. Menurut catatan yang ada, Pythagoras hidup pada abad ke-6 hingga ke-5 SM.

Para ahli dan ilmuwan sejarah bahkan masih memperdebatkan apakah beberapa ajaran filsafat Yunani dan numerologi atas nama pythagoras memang benar gagasannya atau bukan.
Klaim dugaan dari sejarawan matematika, yaitu Pythagoras dan murid-muridnya, adalah orang-orang pertama yang bisa membuktikan rumus teorema phytagoras secara matematis. Selanjutnya, mereka menyebarkannya dalam konteks filosofi dan matematika Yunani kuno.
Tokoh Pythagoras
Sejarah legenda juga sempat menyebutkan bahwa Pythagoras adalah anak dari Mnesarkos, seorang ahli pengukir permata dan merupakan saudagar kaya di Pulau Samos.
Dalam beberapa hal, Pythagoras juga memiliki peran dalam penemuan hal penting lainnya di bidang matematika dan ilmiah. Seperti teori rasio emas atau “golden ratio”, lima bangun ruang, teori kesebandingan, teori bahwa bumi itu bulat, dan lainnya.
Zaman dahulu, ilmu matematika tidak hanya meliputi ilmu numerik atau bilangan melainkan juga untuk menjelaskan seputar filsafat dalam memahami tentang keindahan. Secara tidak langsung, keilmuan Pythagoras pada masanya juga telah mempengaruhi Aristoteles dan Pluto yang merupakan ahli filsafat barat.
Sejarah yang paling populer mengenai rumus teorema pythagoras yaitu segitiga siku-siku yang sering kita dengar dengan sebutan “Segitiga Pythagoras”. Teorema ini pertama kali ada dalam buku Elemen karya matematikawan Yunani kuno, Euclid, sekitar abad ke-3 SM.
Euclid menjelaskan bukti matematis untuk teorema pythagoras. Hal itu adalah salah satu bagian penting dari karyanya dan menjadi pengaruh besar bagi dirinya.
Selama beberapa abad, rumus teorema pythagoras telah menjadi dasar penting dalam ilmu matematika baik di kalangan pelajar maupun di dunia kerja. Penerapannya juga ada dalam beragam bidang kehidupan sebagaimana ada dalam ilmu fisika, numerik hitungan sipil, bangunan, arsitek, dan lainnya.
Jadi, meskipun kita tidak bisa secara paten menyebutkan bahwa Pythagoras adalah seorang penemu teorema itu, Pythagoras dan murid-muridnya memiliki peranan penting dalam mengembangkan dan menyebarkan konsep teorema pythagoras pada masa lalu.
Nama dari “teorema pythagoras” adalah sebagai tanda penghormatan atas kontribusinya di bidang matematika yang mana teorema itu telah mereka buktikan sebelumnya.
Mengenal Apa itu Teorema Pythagoras
Rumus teorema phytagoras memiliki kaitan yang erat dengan segitiga siku-siku dan menyatakan hubungan antara panjang sisi-sisinya. Penulisan simbol sisi-sisi pada segitiga pythagoras yaitu huruf a, b, dan c.
Sisi mendatar dan sisi tegak adalah a dan b, sedangkan sisi miring segitiga siku-siku atau pemilik sudut yang paling besar adalah c (hipotenusa atau sisi miring). Kemudian, p dalil pada Teorema Pythagoras memiliki bunyi sebagai berikut:
“Dalam sebuah segitiga siku-siku, nilai kuadrat panjang sisi miring adalah sama dengan jumlah kuadrat dari panjang sisi-sisi lainnya.”
Baca Juga : Sudut Istimewa Trigonometri: Contoh Soal & Pembahasannya
Rumus Teorema Pythagoras
Pada bentuk matematis, kita bisa menyatakan rumus teorema pythagoras ini sebagai:
c2 = a2 + b2
Penjelasan rumus:
“c” adalah panjang sisi miring (hipotenusa).
“a” dan “b” adalah panjang sisi-sisi lainnya.
Kesimpulannya, teorema ini menyatakan bahwa kuadrat dari panjang sisi miring segitiga siku-siku sama dengan jumlah kuadrat dari panjang sisi-sisi lainnya.
Teorema pythagoras sangat penting dalam matematika. Aplikasinya juga bisa dalam berbagai bidang, seperti ilmu fisika, teknologi rekayasa, dan astronomi. Dengan ini, sangat memungkinkan agar kita bisa tahu panjang salah satu sisi segitiga siku-siku apabila sudah ada data panjang dua sisi lainnya, atau sebaliknya.
Jadi, untuk menghitung rumus sisi mendatar dan sisi tegak dari segitiga siku-siku adalah sebagai berikut:
a2 = c2 – b2
b2 = c2 – a2
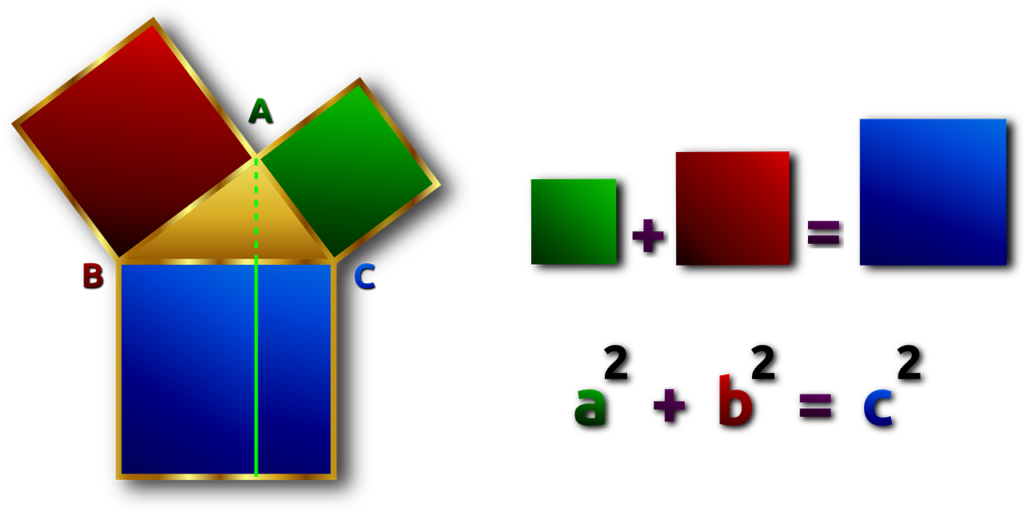
Rumus di atas sesuai bunyi dalil rumus teorema phytagoras, yaitu adanya hubungan geometri antara tiga sisi segitiga siku-siku sehingga kita dapat menyatakan bahwa luas kotak pada sisi miring sama dengan jumlah kotak pada sisi-sisi lainnya.
Contoh Soal Teorema Pythagoras dan Pembahasannya
Pada kesempatan ini, coba pecahkan beberapa permasalahan pada contoh soal di bawah ini dengan menggunakan rumus teorema pythagoras!
1. Contoh Soal 1
Suatu ruangan di sekolah dasar Suka Maju memiliki bentuk segitiga siku-siku. Ruangan itu memiliki dinding tegak (AB) yang tingginya 15 meter, dan sisi dinding mendatarnya (BC) adalah 8 meter. Maka, berapa meter panjang bagian dinding yang miring (AC)?
Pembahasan
Diketahui:
AB = 15 meter
BC = 8 meter
Ditanya:
Panjang AC (meter)?
Jawab:
AC2 = AB2 + BC2
AC2 = 152 + 82
AC2 = 225 + 64
AC2 = 289
AC = √289
√289 = 17 m
Jadi, panjang bagian dinding yang miring adalah 17 meter.
2. Contoh Soal 2
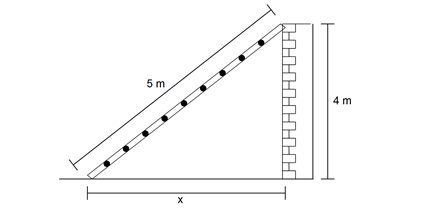
Pak Edgar ingin membuat perosotan untuk Fatimah dengan menggunakan alat yang sudah ada di rumahnya. Apabila bahan yang Pak Edgar pakai untuk membuat sisi miring perosotan panjangnya 5 meter, dan tinggi tangga perosotan itu adalah 4 meter, berapa jarak ujung sisi miring yang menyentuh tanah dengan bagian bawah tangganya?
Pembahasan
Diketahui:
Y (tinggi tangga) = 4 meter
Z (panjang sisi miring) = 5 meter
Ditanya:
Jarak ujung sisi miring dengan bagian bawah tangga (X)?
Jawab:
X2 = Z2 – Y2
X2 = 52 – 42
X2 = 25 – 16
X2 = 9
X = √9 dan √9 = 3 m
Maka, jarak ujung sisi miring yang menyentuh tanah dengan bagian bawah tangga perosotan yaitu 3 meter.
3. Contoh Soal 3
Ismail hobi main layang-layang di lapangan milik pamannya. Ia menaikkan layang-layangnya dengan benang yang panjangnya 50 meter. Jarak Ismail dengan titik yang tepat berada di bawah layang-layang adalah 14 meter. Maka, berapa meter ketinggian layang-layang Ismail sekarang?
Pembahasan
Diketahui:
AB (jarak Ismail dengan titik di bawah layang-layang) = 14 meter
AC (panjang benang) = 50 meter
Ditanya:
BC (tinggi layang-layang dari tanah) dalam meter?
Jawab:
Menggunakan rumus teorema pythagoras,
BC2 = AC2 – AB2
BC2 = 502 – 142
BC2 = 2.500 – 196
BC2 = 2.304
maka, BC = √2.304 dan √2.304 = 48 m
Jadi, ketinggian layang-layang Ismail adalah 48 meter.
Sudah Paham tentang Rumus Teorema Pythagoras?
Melihat dari beberapa contoh soal yang telah kita pelajari, terbukti bahwa rumus teorema pythagoras memiliki manfaat besar bagi kehidupan, bukan? Apa jadinya apabila tidak ada teorema ini? Tentunya lebih rumit bagi kita dalam menentukan suatu nominal angka pada kasus-kasus serupa.
Intinya tidak hanya pada bidang matematika, teorema pythagoras ini juga memberikan kemudahan yang praktis untuk berbagai hal di bidang ilmu lainnya dan kehidupan sehari-hari.

