Turunan fungsi aljabar adalah salah satu konsep penting dalam operasi hitung matematika. Sebab, turunan berguna untuk menggambarkan perubahan suatu fungsi dalam variabel independennya. Dengan menggunakan turunan, kita dapat memahami bagaimana fungsi berubah ketika variabel lainnya berubah.
Konsep ini memiliki berbagai sifat, rumus, dan contoh soal yang berguna dalam mempelajari dan menerapkan turunan dalam berbagai bidang, seperti fisika, ekonomi, dan ilmu komputer. Artikel ini akan menjelaskan semua konsep turunan fungsi aljabar dan memberikan contoh-contoh untuk memperjelas konsep tersebut.
Pengertian Turunan Fungsi Aljabar
Turunan fungsi aljabar adalah konsep dalam kalkulus untuk menghitung perubahan fungsi terkait perubahan variabel inputnya. Evaluasi turunan fungsi pada titik tertentu melibatkan penggunaan aturan-aturan dengan mempertimbangkan batas.
Fungsi f(x) memiliki turunan di setiap titik, yang mana menghasilkan fungsi baru bernama turunan f (dilambangkan dengan f’, df/dx, atau f'(x)). Turunan ini memberikan informasi tentang bagaimana nilai fungsi tersebut berubah saat variabel x berubah, dan dapat dihitung dengan menggunakan berbagai aturan yang ada.
Fungsi aljabar yaitu fungsi dalam bentuk polinomial atau kombinasinya yang melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian. Turunan fungsi aljabar memberi informasi tingkat perubahan fungsi pada tiap titik persamaan diferensial.
Sifat Turunan Fungsi Aljabar

Berikut adalah beberapa sifat-sifat turunan fungsi aljabar yang perlu Anda pahami:
1. Turunan Konstanta
Jika f(x) adalah fungsi konstanta, maka turunannya adalah nol, yaitu f'(x) = 0.
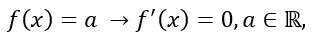
2. Turunan Fungsi Identitas
Secara teori, turunan fungsi identitas akan berlaku jika f(x) = x, maka turunannya adalah 1, yaitu f'(x) = 1.
3. Turunan Fungsi Pangkat
Jika f(x) = xn, dengan n adalah bilangan bulat positif, maka turunannya adalah f'(x) = nx(n-1).
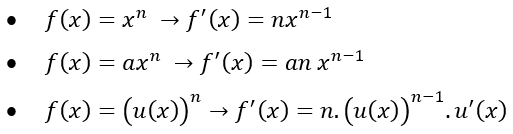
4. Turunan Fungsi Penjumlahan
Jika f(x) = g(x) + h(x), maka turunannya adalah f'(x) = g'(x) + h'(x).
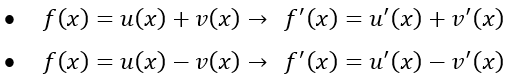
5. Turunan Fungsi Selisih atau Pengurangan
Secara teori, turunan fungsi selisih atau pengurangan akan berlaku jika f(x) = g(x) – h(x), maka turunannya adalah f'(x) = g'(x) – h'(x).
6. Turunan Fungsi Perkalian
Jika f(x) = g(x) . h(x), maka turunannya adalah f'(x) = g'(x) . h(x) + g(x) . h'(x).
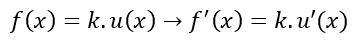
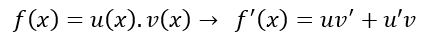
7. Turunan Fungsi Pembagian
Jika f(x) = g(x) / h(x), maka turunannya adalah f'(x) = (g'(x) . h(x) – g(x) . h'(x)) / h(x)2.
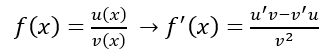
8. Turunan Fungsi Komposisi
Jika f(x) adalah fungsi yang dikomposisikan dengan g(x), maka turunannya dapat dihitung dengan menggunakan aturan rantai (chain rule) yang menggabungkan turunan dari fungsi luar dan fungsi dalam.
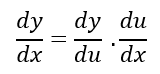
Rumus Turunan Fungsi Aljabar
Dalam matematika, ada satu rumus dasar yang berguna untuk menghitung turunan fungsi aljabar. Berikut adalah rumusnya:
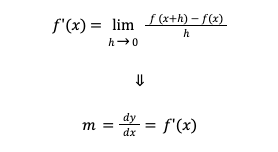
Aplikasi Turunan Fungsi Aljabar
Turunan aljabar ini memiliki banyak aplikasi dalam berbagai bidang matematika, ilmu pengetahuan, teknik, dan ekonomi. Berikut ini adalah beberapa aplikasi umumnya:
1. Persamaan Garis Singgung
Salah satu aplikasi penting dari turunan fungsi aljabar adalah untuk menentukan persamaan garis singgung pada suatu kurva. Garis singgung merupakan garis yang menyentuh kurva pada suatu titik tertentu (a, b) dan memiliki kemiringan (gradien) yang sama dengan turunan fungsi pada titik tersebut, yaitu f'(a).
Garis singgung ini juga dikenal sebagai garis normal, dan gradien garis normal pada titik (a, b) dapat dihitung dengan rumus:
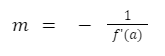
Dengan menggunakan rumus ini, kita dapat menemukan persamaan garis normal pada titik (a, b) pada kurva y = f(x), yang dapat diformulasikan sebagai:
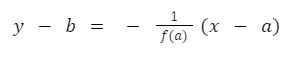
Dengan demikian, turunan fungsi membantu kita dalam menemukan garis singgung atau garis normal pada kurva. Ini merupakan aplikasi penting dalam berbagai konteks matematika dan ilmu terapan lainnya.
2. Menggambar Grafik
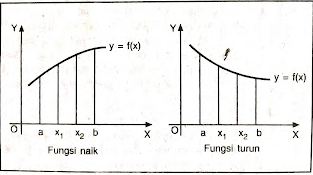
Turunan fungsi aljabar juga sangat berguna dalam menggambar grafik. Penggunaannya pun sangat sederhana dan efektif untuk menentukan kondisi naik atau turunnya grafik suatu fungsi.
Misalnya, jika ada dua titik x1 dan x2 di antara dua nilai a dan b (dengan x1 < x2), dan nilai fungsi pada kurang dari nilai fungsi pada x2. Maka grafik fungsi tersebut naik antara x1 dan x2.
Sebaliknya, jika x1 dan x2 berada di antara a dan b (dengan x1< x2), dan nilai fungsi pada x1 lebih besar dari nilai fungsi pada x2. Maka grafik fungsi tersebut turun antara x1 dan x2.
Kita dapat dengan mudah menggambarkan bagaimana grafik fungsi berperilaku antara dua nilai tertentu dan membantu kita memahami karakteristik grafik dengan cepat dan efisien.
Contoh Soal Turunan Fungsi Aljabar
Berikut adalah beberapa contoh soal tentang turunan fungsi aljabar beserta pembahasannya yang bisa meningkatkan pemahaman kamu:
1. Contoh Soal 1
Temukan turunan dari fungsi x + (1/x)!
Pembahasan:
Misalkan f(x) = x dan g(x) = 1/x. Dengan menggunakan aturan penjumlahan diferensiasi, maka:
d/dx [f(x) + g(x)] = d/dx f(x) + d/dx g(x)
d/dx [x + (1/x)] = d/dx (x) + d/dx (1/x)
= 1 + (-1/x2)
= 1 – (1/x2)
2. Contoh Soal 2
Temukan turunan dari (5x3 – 3x + 1)(x + 1)!
Pembahasan:
Misalkan f(x) = (5x3 – 3x + 1) dan g(x) = (x + 1). Dengan menggunakan aturan produk diferensiasi, maka:
d/dx [f(x) .g(x)] = f(x) [d/dx g(x)] + g(x) [d/dx f(x)]
= (5x3 – 3x + 1) [d/dx (x + 1)] + (x + 1) [d/dx (5x3 – 3x + 1)]
= (5x3 – 3x + 1) (1 + 0) + (x + 1)[5(3x2) – 3(1) + 0]
Kemudian, hitungan akan menjadi:
= (5x3 – 3x + 1) + (x + 1)(15×2 – 3)
= 5x3 – 3x + 1 + 15x3 – 3x + 15x2 – 3
Jadi, hasil akhirnya adalah:
= 20x3 + 15x2 – 6x – 2
3. Contoh Soal 3
Temukan turunan dari sin x – cos x!
Pembahasan:
Misalkan f(x) = sin x dan g(x) = cos x. Dengan menggunakan aturan perbedaan diferensiasi, maka:
d/dx [f(x) – g(x)] = d/dx f(x) – d/dx g(x)
d/dx (sin x – cos x) = d/dx (sin x) – d/dx (cos x)
= cos x – (-sin x)
= cos x + sin x
4. Contoh Soal 4
Temukan turunan dari y = cos (3x -1)!
Pembahasan:
Dengan menggunakan aturan turunan berantai, turunan dari y = cos (3x -1) adalah sebagai berikut:
y = cos (3x -1)
y ‘ = -sin (3x -1) .
Angka 3 diperoleh dari menurunkan 3x -1
Jadi hasil akhirnya yaitu y’ = -3 sin (3x -1)
5. Contoh Soal 5
Temukan turunan dari y = sin (2x + 5)!
Pembahasan:
Dengan mengaplikasikan sifat turunan berantai, maka untuk y = sin (2x + 5) adalah:
y‘ = cos (2x + 5) . 2
Angka 2 diperoleh dari menurunkan 2x + 5. Jadi hasil akhirnya yaitu y’ = 2 cos (2x + 5)
6. Contoh Soal 6
Temukan turunan dari y = sin 2 (2x -1)!
Pembahasan:
Dengan mengaplikasikan sifat turunan berantai, maka untuk y = sin2 (2x -1)
y’ = 2 sin 2-1 (2x -1) . cos (2x -1) . 2
y’ = 2 sin (2x -1) . cos (2x -1) . 2
Jadi hasil akhirnya yaitu y’ = 4 sin (2x -1) cos (2x -1)
Baca Juga : Turunan Fungsi Trigonometri: Pengertian, Rumus, dan Contoh Soal
Sudah Paham Konsep Turunan Fungsi Aljabar?
Dalam matematika, turunan fungsi aljabar memainkan peran penting dalam memahami perubahan dan perilaku fungsi. Dengan menggunakan konsep turunan, kita dapat menghitung tingkat perubahan fungsi pada setiap titik, menentukan gradien garis singgung, menggambarkan grafik fungsi, dan lain sebagainya.
Turunan juga berguna dalam berbagai bidang ilmu, seperti fisika, ekonomi, hingga ilmu komputer untuk menganalisis perubahan dan tren. Dengan mempelajari sifat-sifat turunan dan menguasai rumus-rumusnya, kita dapat mengaplikasikan turunan fungsi aljabar dalam berbagai masalah dan situasi. Dengan demikian, pemahaman tentang turunan fungsi aljabar merupakan pondasi penting dalam mempelajari kalkulus dan matematika lebih dalam lagi. Selamat belajar!

