Mempelajari ilmu matematika tentu tidak terlepas dari berbagai macam rumus dan turunannya. Trigonometri menjadi salah satu bagian ilmu matematika yang cukup kompleks mencakup fungsi sinus, cosinus, tangen, secan, cosecan, dan kotangen. Lebih lanjut, rumus ini juga berkembang menjadi rumus turunan fungsi trigonometri.
Penting bagi Anda untuk memahami terlebih dahulu apa itu fungsi trigonometri dan bagaimana contoh soalnya. Pasalnya, ada banyak sekali rumus yang berbeda-beda. Adanya penurunan fungsi trigonometri ini juga bisa bermanfaat dalam kehidupan sehari-hari. Oleh sebab itu, Anda bisa membaca ulasan di bawah ini sampai selesai.
Pengertian Turunan Fungsi Trigonometri
Turunan atau derivatif merupakan proses perubahan terhadap suatu besaran akibat perubahan dari besaran lainnya. Proses perubahan turunan disebut diferensiasi. Kebalikan turunan yaitu anti turunan.
Sementara itu, turunan fungsi atau diferensial merupakan suatu fungsi lain dari fungsi sebelumnya. Misalnya, fungsi f berubah menjadi f’ dengan nilai tidak beraturan. Ada pula istilah fungsi trigonometri merupakan suatu fungsi yang memuat variabel pada bagian sinus, cosinus, dan tangen.
Fungsi trigonometri memiliki perbandingan yang berada di bagian basis dan tidak berbentuk pangkat. Misalnya f(x) = cos(4x), bukan f(x) = 4cos(x).
Lebih lanjut, turunan fungsi trigonometri merupakan proses turunan yang melibatkan fungsi trigonometri. Turunan pada fungsi ini dapat terjadi dua kali, apabila memiliki koefisien lebih dari satu.
Karakteristik dari Fungsi Dasar Trigonometri
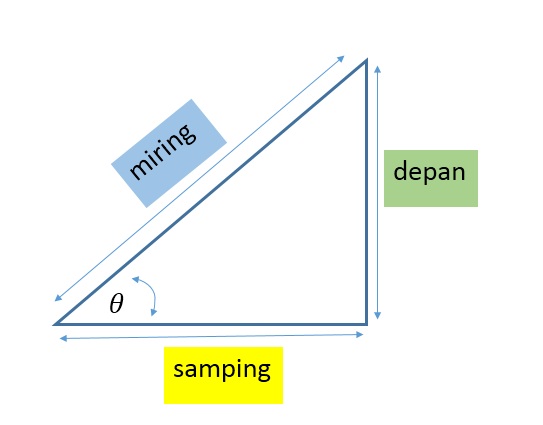
Fungsi utama dari trigonometri adalah sinus, cosinus, dan tangen. Kemudian dapat diturunkan menjadi secan, cosecan, dan kotangen. Karakteristik dari ketiga fungsi dasar trigonometri tersebut yaitu:
1. Sinus (Sin)
Sinus merupakan perbandingan sisi depan sudut segitiga dengan sisi miring pada segitiga siku-siku. Nilai sinus positif berada pada kuadran I dan II, sedangkan nilai sinus negatif di kuadran III dan IV.
2. Cosinus (Cos)
Cosinus merupakan perbandingan sisi miring dengan sisi yang terletak di sudut pada segitiga siku-siku. Nilai cosinus negatif apabila berada di kuadran II dan III, sedangkan nilai cosinus positif berada di kuadran I dan IV.
3. Tangen (Tan)
Tangen adalah perbandingan sisi segitiga yang berada di depan sudut dengan sisi segitiga di bagian sudut pada segitiga siku-siku. Nilai positif tangen terletak di kuadran I dan III, sementara nilai negatif tangen berada di kuadran II dan IV.
Baca Juga : Sudut Istimewa Trigonometri: Contoh Soal & Pembahasannya
6 Rumus Turunan Fungsi Trigonometri
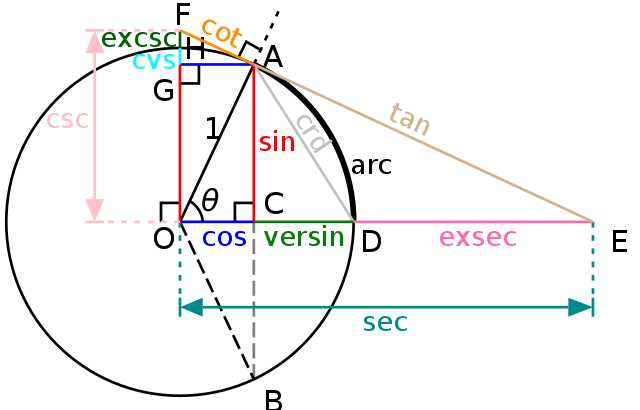
Ketika mempelajari ilmu trigonometri, tentu Anda tidak lupa dengan sinus, kosinus, dan tangen. Turunan fungsi trigonometri juga mencakup tiga hal tersebut, seperti turunan fungsi sinx, turunan terhadap cosx, dan turunan terhadap tanx. Berikut 6 macam rumus untuk memperkuat pemahaman Anda, yaitu:
1. Turunan terhadap Sinx
Apabila fungsi sin x diturunkan terhadap x, maka akan menghasilkan fungsi cos x. Rumusnya yaitu f(x) = sin x maka f’(x) = cos x.
2. Turunan terhadap Cosx
Jika suatu fungsi memuat cosx dan diturunkan terhadap x, maka hasilnya adalah fungsi -sinx. Misalnya, f(x) = cosx maka f’(x) = -sinx.
3. Turunan terhadap Tanx
Selanjutnya, turunan terhadap tanx. Apabila suatu fungsi memuat tanx dan diturunkan terhadap x, maka hasilnya adalah fungsi sec2x. Misalnya, f(x) = tan x maka f’(x) = sec2 x.
4. Turunan terhadap Kotangen x
Rumus turunan dari f (x) = kotangen x adalah f ‘(x) = -cosecan2 x.
5. Turunan terhadap Secan x
Rumus turunan dari f (x) = secan x adalah f ‘(x) = sec x . tan x.
6. Turunan terhadap Cosecan x
Rumus turunan dari f (x) = cosecan x adalah f ‘(x) = -cosecan x . cotangen x.
4 Rumus Identitas Fungsi Trigonometri
Selain rumus dasar di atas, ada pula beberapa rumus identitas yang bisa Anda gunakan untuk menyelesaikan soal yang berkaitan dengan fungsi trigonometri. Berikut 4 macam rumusnya, yaitu:
1. Rumus Identitas Perbandingan
Tan (nx) = sin (nx) / cos (nx) sama dengan cot (nx) = cos (nx) / sin (nx).
2. Rumus Sinus Sudut Rangkap
Sin (nx) = 2 sin (n/2 x) cos (n/2 x)
3. Rumus Kosinus Sudut Rangkap
Cos (nx) = 1 – 2 sin2 (n/2 x)
4. Rumus Identitas Phytagoras
Sin2 (nx) + cos2 (nx) = 1
tan2 + 1 = sec2 (nx)
tan 2 + 1 = cosec22 (nx)
7 Contoh Soal dan Pembahasan

Anda sudah memahami berbagai bentuk rumus turunan fungsi trigonometri pada ulasan sebelumnya? Berikut 7 contoh soal beserta pembahasannya untuk mendukung pemahaman Anda agar lebih jelas, yaitu:
Contoh 1
Diketahui y = -2 cos x. Tentukan nilai y’!
Pembahasan:
y = -2 cos x
y’ = -2 (-sin x)
= 2 sin x
Jadi, turunan dari y = -2 cos x adalah y’ = 2 sin x.
Contoh 2
Tentukan turunan pertama dari y = -4 sin x!
Pembahasan:
Penyelesaian soal ini mengacu pada rumus turunan trigonometri yang pertama, yaitu f(x) = sin x.
maka,
y = -4 sin x.
y’ = -4 cos x.
Jadi, nilai turunan pertama dari y = -4 sin x adalah y’ = -4 cos x.
Contoh 3
Tentukan turunan dari y = 5 cos x -3 sin x.
Pembahasan:
y = 5 cos x -3 sin x
y’ = 5 (-sin x) – 3 (cos x)
= -5 sin x -cos x
Maka, turunan dari y = 5 cos x -3 sin x adalah y’ = -5 sin x -cos x.
Contoh 4
Tentukan nilai y’ dari y = 4 sin x + 5 cos x.
Pembahasan:
y = 4 sin x + 5 cos x
y’ = 4 (cos x) + 5 (-sin x)
= 4 cos x -5 sin x
Jadi, turunan dari y = 4 sin x + 5 cos x adalah y‘ = 4 cos x -5 sin x
Contoh 5
Diketahui f(x) = sin(2x + 10), berapakah nilai turunan fungsinya?
Pembahasan:
Penyelesaian pada soal ini mengacu pada rumus dasar f(x) = sin(ax + c) dan turunannya f’(x) = a cos(ax + c).
Maka, f(x) = sin(2x + 10)
f’(x) = 2cos(2x + 10)
Jadi, nilai turunan fungsi dari f(x) = sin(2x + 10) adalah f’(x) = 2cos(2x + 10).
Contoh 6
Diketahui suatu fungsi dengan perbandingan berpangkat f(x) = 2sin2(5x2 + 6). Berapakah nilai turunannya?
Pembahasan:
Untuk penyelesaian jenis soal ini, Anda bisa menggunakan rumus dasar turunan fungsi trigonometri f(x) = k . sinn(ax + b) dengan hasil turunan f’(x) = k . na . sinn – 1 (ax + b).cos(ax + b).
Maka, penyelesaiannya yaitu:
f(x) = 2sin2(5x2 + 6)
f’(x) = 2 (2) (10x) sin(5x2 + 6)cos(5x2 + 6)
Jadi, turunan dari f(x) = 2 sin2(5x2 + 6) adalah f’(x) = 2 (2) (10x) sin(5x2 + 6)cos(5x2 + 6).
Contoh 7
Tentukan turunan dari y = cos (3x -1)
Pembahasan:
Penyelesaian soal ini mengacu pada aplikasi turunan berantai yaitu:
y = cos (3x -1)
y’ = – sin (3x -1) . 3
Angka 3 di belakang berasal dari hasil turunan 3x – 1
y’ = – 3 sin (3x -1)
Jadi, hasil turunan dari y = cos (3x -1) adalah y’ = – 3 sin (3x -1).
Baca Juga : Turunan Fungsi Trigonometri: Pengertian, Rumus, & Contoh Soal
7 Pengaplikasian Turunan Fungsi Trigonometri
Penggunaan rumus trigonometri dan turunannya ternyata tidak hanya untuk menyelesaikan soal-soal matematis saja. Ada beberapa pengaplikasian turunan ini dalam kehidupan sehari-hari. Berikut ini 7 contohnya, yaitu:
1. Memperkirakan suhu tertinggi dan terendah di berbagai negara yang memiliki empat musim.
2. Memperkirakan puncak arus mudik lebaran untuk mengantisipasi terjadinya kemacetan di jalan.
3. Menentukan jarak optimal antara tempat duduk dan layar di bioskop.
4. Menentukan papan terpendek untuk menopang pagar rumah.
5. Memperkirakan waktu yang optimal untuk proses produksi suatu barang agar dapat meningkatkan penjualan.
6. Menentukan kemiringan garis singgung kurva trigonometri y = f(x).
7. Menentukan nilai maksimal dan minimal dari suatu fungsi tertentu.
Sudah Paham Rumus Turunan Fungsi Trigonometri?
Secara keseluruhan, ada banyak rumus turunan fungsi trigonometri. Anda bisa memahami 7 contoh soal di atas untuk mengetahui cara menghitung dari masing-masing rumus. Fungsi trigonometri ini tidak terlepas dari fungsi sinus, cosinus, dan tangen. Namun, Anda juga bisa mengaplikasikannya dalam kehidupan sehari-hari.

