Turunan Fungsi Trigonometri: Pengertian, Rumus, & Contoh Soal

Trigonometri merupakan studi yang berhubungan dengan sudut dalam segitiga. Dalam studi ini, terdapat turunan fungsi trigonometri yang berkaitan dengan beberapa fungsi di dalamnya, seperti cos, sin, dan tan.

Seperti yang diketahui, fungsi-fungsi tersebut memiliki peranan penting dalam studi kasus trigonometri. Untuk lebih jelasnya, mari simak pembahasannya berikut ini beserta beberapa contoh soal dan pembahasannya.

Apa Itu Turunan Fungsi Trigonometri?

Menurut Sutisna dalam Modul Matematika Kelas XII, trigonometri merupakan salah satu cabang ilmu matematika yang berhubungan dengan sudut segitiga. 

Pada studi ini terdapat beberapa fungsi, seperti sin, cos, dan tan. Sementara turunan yang dimaksud adalah perubahan pada fungsi trigonometri tersebut. 

Artinya, turunan fungsi trigonometri adalah sebuah proses dalam memperoleh turunan pada suatu fungsi trigonometris. Misalnya, pada f(x) berubah menjadi f'(a).

Sejarah Turunan Fungsi Trigonometri

Awal mula perkembangan turunan fungsi trigonometris berkaitan erat dengan perkembangan studi kalkulus. Konsep ini diutarakan oleh Newton (1642-1727) dan Gottfried Wilhelm Leibniz (1646-1716). Keduanya merupakan ahli matematika yang berasal dari Inggris dan Jerman.

Perkembangan kalkulus terbagi dalam beberapa era. Pemikirannya pertama kali diutarakan pada zaman kuno. 

Pada saat itu, kalkulus berguna untuk melakukan perhitungan volume dan luas dan berkembang di Mesir. Orang Mesir menggunakannya untuk menghitung piramida yang mereka dirikan.

Selanjutnya pada zaman pertengahan, seorang matematikawan yang berasal dari India. Konsep kalkulus berguna untuk menunjukkan masalah astronomi. Kondisi ini merupakan awal perkembangan bentuk turunan.

Pada abad ke 12, seorang ahli dari Persia menemukan turunan fungsi kubik. Selanjutnya, Newton dan Leibniz mengembangkan penemuan tersebut dan menentukan gagasan sebagai kalkulus. Keduanya disebut sebagai penemu dalam waktu yang bersamaan secara terpisah.

Seiring berkembangnya zaman, turunan memiliki banyak aplikasi. Seperti yang dikemukakan Newton dalam hukum gerak menyatakan, turunan momentum suatu benda sama dengan gaya yang diberikan.

Sementara dalam bidang ekonomi, turunan juga berguna memberikan strategi terbaik ketika terjadi sebuah persaingan. Turunan dapat membantu menghitung seberapa efektif waktu dan tenaga kerja untuk meminimalisir biaya dan memaksimalkan keuntungan.

Fungsi Trigonometri yang Kerap Muncul 

Fungsi trigonometri memiliki beberapa karakteristik khusus yang membedakannya. Adapun 3 fungsi trigonometri yang kerap muncul adalah sebagai berikut, yaitu:

1. Sinus (Sin) 

Sinus merupakan salah satu fungsi trigonometri dengan perbandingan sudut segitiga pada sisi depan dan sisi miring. Fungsi ini berguna ketika sudut segitiga berbentuk siku-siku atau memiliki sudut sebesar 90 derajat.  

Pada kuadran, fungsi sinus dapat bernilai negatif maupun positif. Sinus yang bernilai positif terletak pada kuadran I dan II, sementara yang bernilai negatif terletak di kuadran III dan IV.

2. Cosinus (Cos) 

Fungsi selanjutnya adalah cosinus. Cosinus merupakan perbandingan pada sisi segitiga antara sudut dan sisi miring. Fungsi cosinus hanya berlaku pada segitiga siku-siku atau segitiga yang salah satu sudutnya berukuran 90 derajat.

Seperti halnya sinus, cosinus juga dapat bernilai negatif dan positif. Nilai negatifnya terletak pada kuadran II dan III, sedangkan nilai positifnya terletak pada kuadran III dan IV.

3. Tangen (Tan) 

Fungsi trigonometris terakhir adalah tangen. Tangen merupakan perbandingan pada sisi segitiga yang berada di depan sudut. Seperti halnya fungsi cosinus, fungsi ini juga berlaku pada segitiga siku-siku.

Sementara untuk nilai positif fungsi ini di kuadran adalah terletak di kuadran I dan III. Nilai negatifnya adalah terletak di kuadran II dan IV.

Rumus Turunan Fungsi Trigonometri

Adapun rumus pada turunan fungsi trigonometri adalah sebagai berikut:

• Turunan dari f (x) = sin x adalah f ‘(x) = cos x.
• Turunan dari f (x) = cos x adalah f ‘(x) = -sin x.
• Turunan dari f (x) = tan x adalah f ‘(x) = sec2 x.
• Turunan dari f (x) = tangen x adalah f ‘(x) = -sec2 x.
• Turunan dari f (x) = secan x adalah f ‘(x) = sec x . tan x.
• Turunan dari f (x) = secan x adalah f ‘(x) = -cosec x . cotangen x.

Rumus Perluasan Turunan Fungsi Trigonometri

Tidak hanya rumus dasar, juga terdapat rumus perluasan pada turunan fungsi trigonometri. Rumus perluasan berguna apabila terdapat beberapa kondisi tertentu. Berikut adalah penjabaran dari rumus perluasan.

Rumus perluasan turunan fungsi trigonometri I

• Turunan dari f (x) = sin u adalah f ‘(x) = cos u . u’.
• Turunan dari f (x) = cos u adalah f ‘(x) = -sin u . u’.
• Turunan dari f (x) = tan u adalah f ‘(x) = sec2u . u’.
• Turunan dari f (x) = cot u adalah f ‘(x) = -csc2 u . u’.
• Turunan dari f (x) = sec u adalah f ‘(x) = sec u tan u . u’.
• Turunan dari f (x) = csc u adalah f ‘(x) = -csc u cot u . u’.

Rumus perluasan turunan fungsi trigonometri II

• Turunan dari f (x) = sin (ax + b) adalah f ‘(x) = a cos (ax + b).
• Turunan dari f (x) = cos (ax + b) adalah f ‘(x) = -a sin (ax + b).
• Turunan dari f (x) = tan (ax + b) adalah f ‘(x) = a sec2 (ax +b).
• Turunan dari f (x) = cot (ax + b) adalah f ‘(x) = -a csc2 (ax+b).
• Turunan dari f (x) = sec (ax + b) adalah f ‘(x) = a tan (ax + b) . sec (ax + b).
• Turunan dari f (x) = csc (ax + b) adalah f ‘(x) = -a cot (ax + b) . csc (ax + b).

Aplikasi Turunan Fungsi Trigonometri dalam Kehidupan 

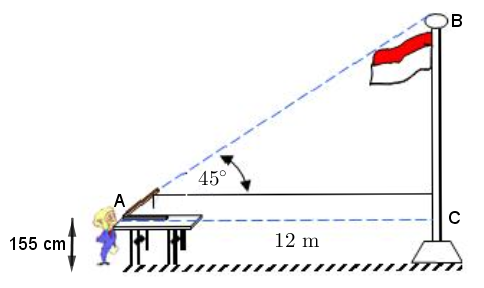
Turunan trigonometri memiliki dapat diaplikasikan dalam kehidupan sehari-hari, diantaranya adalah sebagai berikut.

• Berguna dalam menentukan jarak tempat duduk pada bioskop.
• Membantu menentukan ukuran papan yang berguna untuk menopang pagar.
• Membantu mengetahui kemiringan grafik. 
• Membantu mengetahui perkiraan puncak arus mudik, sehingga dapat mengantisipasi kemacetan. 
• Membantu meminimalisir pengeluaran dan berguna untuk memaksimalkan keuntungan.
• Mengetahui kondisi cuaca.

Baca Juga : Sudut Istimewa Trigonometri: Contoh Soal & Pembahasannya

5 Contoh Soal dan Pembahasannya

Berikut adalah 5 contoh soal fungsi trigonometri lengkap dengan pembahasannya, yaitu:

Contoh 1

Turunkan fungsi berikut ini.

y = 5 sin x

Pembahasan:

y = 5 sin x
y’ = 5 cos x

Jadi, turunan fungsi y = 5 sin x adalah  y’ = 5 cos x.

Contoh 2

Tentukan turunan dari y = -8 sin x.

Pembahasan:

y = -8 sin x.
y’ = -8 cos x.

Jadi, turunan fungsi y = -8 sin x adalah y’ = -8 cos x.

Contoh 3

Berapa turunan y’ dari y = 5 sin x + 6 cos x.

Pembahasan:

y = 5 sin x + 6 cos x
y’ = 5 (cos x) + 6 (-sin x) = 5  cos x -6 sin x

Berdasarkan soal di atas, maka turunan fungsi dari y = 5 sin x + 6 cos x adalah y’ = 5  cos x -6 sin x.

Contoh 4

Berapa turunan dari y = cos (2x -1)

Pembahasan:

Dengan aplikasi turunan berantai, maka untuk

y = cos (2x -1)
y ‘ = -sin (2x -1) . 2 -> Angka 2 diperoleh dari menurunkan 3x -1
Hasil akhirnya adalah y’ = -2 sin (2x -1)

Contoh 5

Tentukan turunan dari y = sin² (3x -1).

Pembahasan:

Turunan berantai:

y = sin² (3x -1)
y’ = 3 sin ^2-1 (3x -1) . cos (3x -1) . 3
y’ = 3 sin (3x -1) . cos (3x -1) . 3
y’ = 9 sin (3x -1) cos (3x -1)

Sudah Tahu Turunan Fungsi Trigonometri?

Itulah pembahasan mengenai turunan fungsi trigonometri. Setelah memahaminya, dapat kita ketahui studi ini memiliki beberapa peranan penting dalam kehidupan sehari-hari. 

Bahkan cakupan pembahasannya juga dapat berkaitan dengan ilmu studi lainnya, seperti ekonomi, fisika, dan astronomi. Selain itu, dalam perkembangannya dengan adanya turunan ini akan dapat membantu menjabarkan fungsi trigonometri pada tahap yang lebih lanjut.