Dalam matematika, pemahaman tentang sumbu simetri sangat penting untuk mengenali pola dan memahami struktur geometris bangun datar. Walau demikian, tidak semua orang tahu cara menentukan sumbu simetri bangun datar yang benar.
Jika Anda adalah salah satunya dan sedang ingin mempelajarinya, maka Anda sudah datang ke tempat yang tepat. Mari kita jelajahi lebih lanjut tentang cara menentukan sumbu simetri bangun datar dan contoh penerapannya di artikel ini!
Apa Itu Sumbu Simetri Bangun Datar?
Secara istilah, sumbu simetri bangun datar menjelaskan dua frasa berbeda, yaitu sumbu simetri dan bangun datar. Sehingga, definisi dari sumbu simetri bangun datar akan mencerminkan arti dari kedua istilah tersebut. Lantas, apa itu sumbu simetri dan bangun datar secara terpisah?
Sumbu simetri adalah garis imajiner dalam sebuah objek atau bangun geometri, seperti bangun datar dan bangun ruang, yang membagi objek menjadi dua bagian yang sama persis. Jika objek dilipat, maka kedua bagian akan tumpang tindih satu sama lain.
Bangun datar merupakan bentuk geometri dua dimensi yang terdiri dari garis-garis, titik-titik, dan sudut-sudut. Contoh bangun datar meliputi segitiga, persegi, persegi panjang, lingkaran, trapesium, layang-layang, jajar genjang, dan lain sebagainya.
Bangun datar memiliki sifat-sifat khusus, seperti panjang sisi, sudut, luas, dan keliling, yang dapat berguna untuk mengidentifikasi dan membandingkan bangun datar tersebut.
Berdasarkan definisi masing-masing istilah, sumbu simetri bangun datar adalah garis imajiner yang membagi bangun datar menjadi dua bagian yang simetris. Ini berarti kedua bagian tersebut memiliki bentuk, ukuran, dan posisi yang sama persis.
Sumbu simetri dapat berbeda-beda tergantung pada jenis bangun datar yang sedang Anda amati. Dengan cara menentukan sumbu simetri bangun datar, Anda dapat memahami sifat simetri dan memahami bagaimana bangun datar tersebut terorganisir secara visual.
Cara Menentukan Sumbu Simetri Bangun Datar dan Nilai Optimum
Menentukan sumbu simetri dalam bangun datar adalah langkah penting dalam geometri. Berikut adalah panduan tentang cara menentukan sumbu simetri bangun datar beserta nilai optimumnya:
1. Sumbu Simetri
Simetri mengacu pada keseimbangan antara bagian-bagian yang saling berlawanan atau berpasangan dalam sebuah objek atau bangun. Misalnya, pada tubuh manusia, jika Anda menggambar garis dari kepala, hidung, mulut, dan pusar hingga ke bawah, maka Anda akan melihat bahwa bagian kanan dan kiri memiliki kesamaan.
Terdapat mata kanan dan mata kiri, telinga kanan dan telinga kiri, tangan kanan dan tangan kiri, kaki kanan dan kaki kiri, dan seterusnya. Jika sebuah bangun datar dapat dilipat sehingga sisi-sisinya saling berhimpit dengan sempurna, maka bangun tersebut memiliki simetri lipat.
Garis lipatan tersebut dapat Anda sebut sebagai sumbu simetri lipat. Jumlah sumbu simetri lipat sama dengan jumlah simetri lipat yang dimiliki oleh bangun datar tersebut. Bangun datar yang dapat terlipat menjadi dua bagian sama besar dan berhimpit dengan tepat dapat Anda kenal sebagai bangun datar simetris.
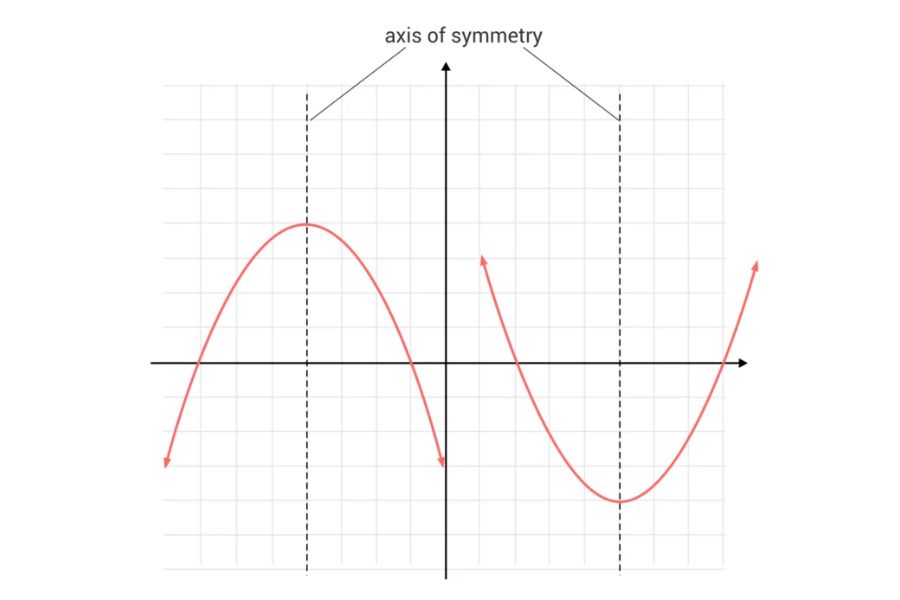
Dalam buku “Genius Matematika Kelas 5 SD” karya Sulis Sutrisna, sumbu simetri didefinisikan sebagai garis yang ditarik di bidang datar sehingga membagi bidang menjadi dua bagian yang sama dan sebangun. Pada grafik fungsi kuadrat, sumbu simetri berfungsi sebagai garis pantulan dari titik pada grafik fungsi kuadrat tersebut.
Adapun ciri-ciri bangun datar yang memiliki simetri adalah memiliki simetri lipat dan dapat dilipat atau dibagi menjadi dua bagian yang sama besar. Lantas, bagaimana cara menentukan sumbu simetri bangun datar?
Misalkan Anda memiliki sebuah persegi dengan titik sudut A, B, C, dan D. Jika Anda melipat sisi AB ke CD, maka lipatan akan terjadi dengan rapi dan presisi. Hal yang sama terjadi jika Anda melipat sisi AC ke BD.
Lipatan juga akan terjadi tanpa ada yang berlebihan. Dengan demikian, Anda dapat mengetahui bahwa persegi memiliki dua sumbu simetri lipat, yaitu AB ke CD dan AC ke BD.
2. Nilai Optimum
Menurut Yuliansyah dalam buku “Buku Penunjang Bahan Ajar Matematika”, nilai optimum merujuk pada nilai yang mencapai nilai tertinggi (maksimum) atau nilai terendah (minimum). Nilai maksimum atau minimum ini sering kali disebut sebagai objektif, fungsi objektif, fungsi tujuan, atau fungsi sasaran.
Dalam konteks fungsi kuadrat, nilai optimum dalam konsep cara menentukan sumbu simetri bangun datar dapat Anda hitung menggunakan rumus berikut:
y = -D/4a
Jumlah Bentuk Bidang Sumbu Simetri
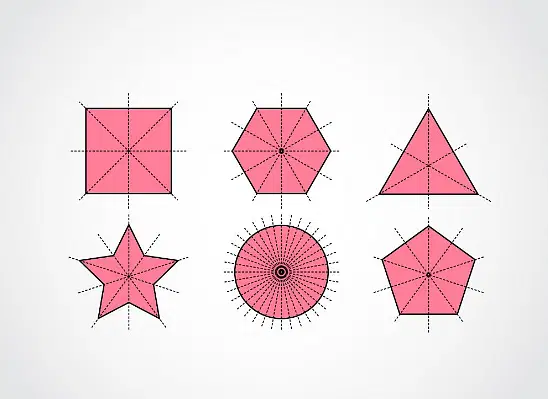
Berikut adalah jumlah sumbu simetri untuk berbagai jenis bangun datar yang perlu Anda pahami:
- Lingkaran dengan jumlah sumbu simetri tak terhingga.
- Jajar genjang tidak memiliki sumbu simetri.
- Sama kaki trapesium memiliki 1 sumbu simetri.
- Trapesium siku-siku dan trapesium apa pun tidak memiliki sumbu simetri.
- Persegi panjang memiliki 2 sumbu simetri.
- Segitiga sama sisi memiliki 3 sumbu simetri.
- Segitiga sama kaki memiliki 1 sumbu simetri.
- Segitiga sembarang tidak memiliki sumbu simetri.
- Persegi memiliki 4 sumbu simetri.
- Belah ketupat memiliki 2 sumbu simetri.
- Layang-layang memiliki 1 sumbu simetri.
Penting untuk Anda pahami bahwa jumlah sumbu simetri dalam bentuk datar membagi bentuk tersebut menjadi dua, tiga, empat, dan seterusnya. Dengan pemahaman ini, Anda dapat mengetahui cara menentukan sumbu simetri bangun datar tanpa perlu menghafalnya.
Baca Juga : Mengenal Perbedaan Sumbu Simetri Lipat dan Simetri Putar
Contoh Soal dari Cara Menentukan Sumbu Simetri Bangun Datar
Supaya Anda bisa memahami cara menentukan sumbu simetri bangun datar dengan lebih mendalam, simak beberapa contoh soal di bawah ini:
1. Contoh Soal 1
Berapakah sumbu simetri, nilai puncak, dan koordinat puncak dari fungsi kuadrat f(x) = 4x2 – 8x + 3?
Pembahasan:
Diketahui terdapat fungsi kuadrat: f(x) = 4x2 – 8x + 3. Anda diminta untuk mencari sumbu simetri, nilai optimum, dan titik optimum dari fungsi tersebut.
Nah, untuk mencari sumbu simetri, Anda bisa menggunakan rumus x = -b/2a. Dalam fungsi ini, a = 4 dan b = -8. Dengan menggantikan nilai a dan b ke rumus sumbu simetri, Anda dapat menghitungnya menjadi:
x = -(-8) : (2 x 4)
x = 8 : 8 = 1
Jadi, sumbu simetri adalah x = 1.
Kemudian, untuk mencari nilai optimum, gunakan rumus y = -D/4a atau dengan memasukkan nilai x ke fungsi. Carilah nilai optimum dengan memasukkan nilai x:
f(1) = 4(1)2 – 8(1) + 3
f(1) = 4 – 8 + 3 = -1
Jadi, nilai optimum dari fungsi tersebut adalah -1.
Sedangkan untuk menentukan titik optimum atau titik di mana fungsi mencapai nilai optimumnya, Anda dapat menjabarkan titik optimum menjadi (1, -1). Sebab, nilai x adalah 1 dan nilai y adalah -1.
2. Contoh Soal 2
Cermatilah gambar berikut ini!
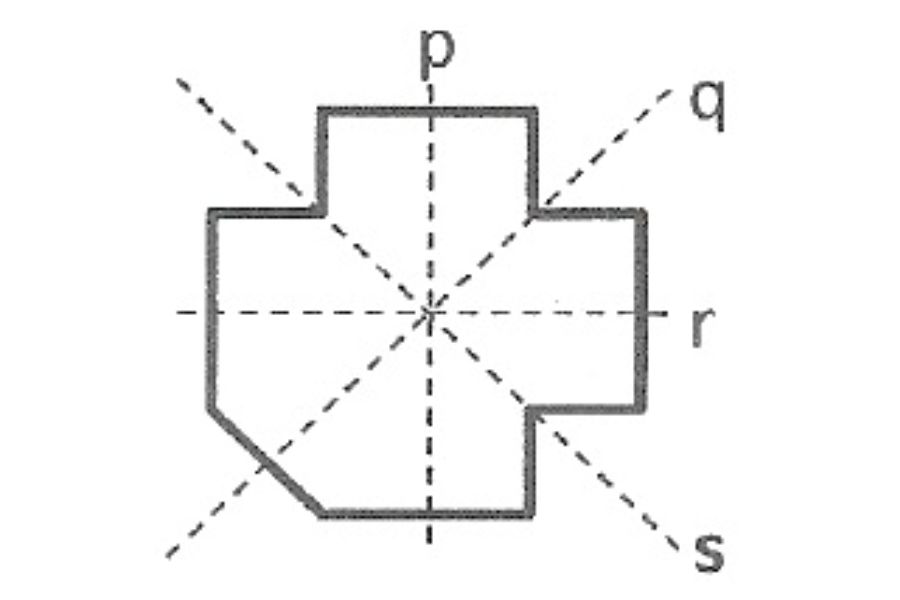
Dengan mengacu pada cara menentukan sumbu simetri pada bangun datar, garis mana yang menunjukkan sumbu simetri?
A. Garis p
B. Garis q
C. Garis r
D. Garis s
Pembahasan:
Jawabannya adalah B. Sebab, garis q adalah sumbu simetri yang membagi bangun tersebut menjadi dua bagian yang sama besar.
Baca Juga : Rumus Sumbu Simetri, Cara Menentukan, dan Contoh Soal
Cara Menentukan Sumbu Simetri Bangun Datar Itu Mudah, Bukan?
Dalam menentukan sumbu simetri bangun datar, Anda dapat menggunakan prinsip bahwa sumbu simetri membagi bangun datar menjadi dua bagian yang sama. Dengan mengetahui cara menentukan sumbu simetri pada bangun datar, Anda dapat memahami sifat simetris dan memanfaatkannya dalam berbagai penerapan.
Contohnya, sumbu simetri pada lingkaran berguna dalam membuat pola-pola simetris, seperti pola bunga atau pola geometri. Penerapan sumbu simetri juga dapat berguna dalam desain grafis, arsitektur, dan berbagai bidang lainnya untuk mencapai keseimbangan visual yang estetis dan harmonis.

